Второй отборочный раунд и его разбор были подготовлены rng_58, snuke, snarknews и Gassa.

Во втором раунде турнира «Яндекс.Алгоритм» хотя бы одну попытку сделало 495 участников, хотя бы одну задачу из них решило 425. По задаче A было сделано 503 попытки, из них 73 успешных, по задаче B — 11 попыток (2 успешных), по задаче C — 472 попытки (76 успешных), по задаче D — 846 попыток (386 успешных), по задаче E — 42 попытки (16 успешных) и по задаче F — 624 попытки (182 успешных).

Результаты тестового прорешивания позволяли надеяться на то, что количество участников, сдавших 5 задач, будет выше, чем в первом раунде, и что победители сдадут по 6 задач. Однако оценка оказалась завышенной. Ближе к середине раунда определились двое лидеров — tourist и eatmore, сдававшие все задачи «втёмную». Далее шла целая группа преследователей, у каждого из которых было сдано не более двух задач «втёмную». Первым сдал 5 задач cgy4ever из Китая, у которого задача C была сдана «втёмную»; на 75-й минуте по 5 задач сдали maciej.klimek (maciejk) из Польши, Jedi_Knight (ivan.popelyshev) и burunduk3. На 77-й минуте пятую задачу сдаёт tourist и выходит на первое место с пятью задачами «втёмную». На 80-й минуте свою пятую задачу, причём также «втёмную» сдаёт eatmore; это оказывается задача B, которую до этого не сдал ни один участник. Тем не менее, tourist удерживает лидерство. За минуту до завершения контеста задачу E, ставшую для неё пятой, сдаёт natalia и с четырьмя задачами «втёмную» из пяти выходит на третье место.

После системных тестов выясняется, что в первой тройке сумел удержаться только tourist, у которого прошли все 5 «тёмных» попыток. Впрочем, он уже обеспечил себе участие в финале по итогам первого отборочного раунда, так что «проходным» становилось пятое место. У eatmore не прошла задача E, которую он сдавал предпоследней; у natalia — задача F, которую она также сдавала предпоследней. Зато последние отправленные задачи — решённая только двумя участниками (кроме eatmore, это s-quark из Китая) B для eatmore и отправленная на 1:39 E для natalia — системное тестирование прошли.

В результате второе место занял vepifanov, третье — yeputons, сдавшие «втёмную» только задачу D на 5-й минуте. Все последующие участники сдавали все задачи «в открытую». Четвёртое место занял Jedi_Knight (ivan.popelyshev), пятое, последнее из «проходных»,— peter50216 из Тайваня.

Задача A (Степени вершин)

Заметим, что если сумма всех d_i не равна 2(N - 1), то d не может быть последовательностью степеней вершин дерева, поэтому нужно вывести «None». В противном случае, несложно доказать, что всегда существует дерево, для которого d является последовательностью степеней вершин.

Пусть c — количество таких i, что d[i] ≥ 2. Есть несколько случаев:

1. c = 0. В этом случае d = {1, 1}. Очевидно, ответ — «Unique».
2. c = 1. Дерево должно быть «звездой». Ответ снова «Unique».
3. c = 2. Есть две вершины степени  ≥ 2. Обозначим их s и t. Должно быть ребро, соединяющее s и t, а все остальные ребра соединяют одну из вершин {s, t} с листом. Таким образом, ответ снова «Unique».
4. c = 3. Есть три вершины степени  ≥ 2. Обозначим их s, t и u. Рассмотрим три пары вершин {s, t}, {t, u} и {u, s}. Ровно две из них должны быть соединены ребром (если все три соединены ребром, то в графе образуется цикл; если одна или менее пар соединены ребром, то граф становится несвязным), поэтому есть три способа их соединить. Если степени вершин s, t, u все совпадают, все три получающихся дерева изоморфны, поэтому ответ — «Unique». Иначе ответ — «Multiple».
5. c ≥ 4. Если последовательность степеней, отсортированная по возрастанию, имеет вид {1, 1, 2, ..., 2}, то дерево должно быть цепочкой, поэтому ответ — «Unique». Иначе есть хотя бы одна вершина степени  ≥ 3. Можно построить два неизоморфных дерева, используя эту вершину: один способ — это составить цепочку вершин степени >=2 и прикрепить к ним листья, а другой — соединить три цепочки в одной общей вершине. В этом случае ответ — «Multiple».

Задача B (Лягушки)

Пусть f(t) — позиция лягушки k в момент времени t. Нас просят найти минимальное такое t, что t - f(t) ≥ d. Заметим, что t - f(t) — неубывающая функция, так как для любого t значение f(t + 1) - f(t) — это 0 или 1. Так как t - f(t) монотонно, мы можем использовать бинарный поиск. Основная часть решения состоит в подсчете f(t).

Предположим для простоты, что k = 2 (в противном случае мы можем повторить аналогичный алгоритм k - 1 раз). Назовем число n хорошим, если сумма высот между кочками 1 и n делится на m. «Хорошесть» имеет период m(p - 1), то есть n — хорошее тогда и только тогда, когда 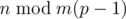— хорошее. Рассчитаем и запомним в таблице для каждого n ≤ m(p - 1), является ли оно хорошим. Получается, что f(t) — это (количество хороших чисел между 1 and t), поэтому мы можем быстро вычислить его, используя таблицу.

Задача C (Зеленый треугольник)

Мы хотим посчитать сумму ориентированных площадей треугольников pqr для всех троек (p, q, r), перечисленных по часовой стрелке. Если зафиксировать точки p и q, ориентированная площадь треугольника pqr будет линейной функцией координат точки r, поэтому нам достаточно знать сумму всех абсцисс и сумму всех ординат всех точек в одной полуплоскости относительно прямой pq.

Зафиксируем точку p. Отсортируем все остальные точки по часовой стрелке относительно точки p и обозначим их в этом порядке p₀, ..., p_n - 2. Тогда мы можем использовать алгоритм двух указателей: будем поддерживать два индекса i и j. Здесь j — это наибольший индекс, удовлетворяющий условию «три точки p, p_i, p_j перечислены по часовой стрелке». Мы растим i от 0 до n - 2 и поддерживаем j. Когда мы увеличиваем i, j никогда не уменьшается, поэтому суммарное количество изменений i и j ограничено O(n). Суммарно алгоритм работает за время .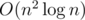

При указанных в задаче ограничениях на координаты возникают проблемы с точностью во время вычисления площади: точности double в случае треугольников малой площади, но большого периметра не хватает. Особенно эта проблема актуальна для Java, где тип long double отсутствует, а при использовании встроенного типа BigInteger решение не укладывается в Time Limit.

В качестве варианта рекомендуется при вычислении хранить сумму площадей для фиксированного основания треугольника как в double, так и в 64-битном целом: тогда по double определяются старшие 52 бита результата, а в 64-битном целом хранятся младшие 64 бита.

Задача D (MathWorlds)

Это самая простая задача. Нужно перебрать все операторы и посчитать количество операторов, удовлетворяющих условию «x <оператор> y = z». Особо надо рассмотреть случай y = 0, например, вообще исключив при y = 0 проверку оператора деления. Вариант «привести деление к умножению» не работает, например, для теста 0 0 1, который создал проблемы многим участникам.

Задача E (Маленькие циклы)

Свойства в условии задачи эквивалентны следующему:

1. У G есть остовное дерево. Зафиксируем какое-нибудь остовное дерево T и назовем ребра T «ребрами дерева», а остальные — «внешними ребрами».
2. Если e = {u, v} — внешнее ребро, то расстояние между u и v в T равно двум.
3. Для каждого внешнего ребра e = {u, v} покрасим путь между u и v в T. Тогда никакое ребро не покрашено дважды..

Исходная задача сводится к следующей: дано дерево, и некоторые ребра в нем покрашены. На каждом шаге можно выбрать путь длины 2 и покрасить его (при этом нельзя красить ребро, если оно уже покрашено). Какое максимальное количество шагов можно сделать?

Эта задача может быть решена жадно. «Подвесим» дерево за какую-нибудь вершину и найдем самое глубокое неокрашенное ребро e. Если у ребра e нет соседних неокрашенных ребер, то его покрасить невозможно — проигнорируем его. Если у ребра e есть соседнее неокрашенное ребро (обозначим его e₂) из той же вершины-родителя, то нужно покрасить e и e₂ одновременно, иначе мы не сможем покрасить оба ребра. Если у ребра e есть только соседнее ребро, ведущее в вершину-родителя e в свою очередь из ее вершины-родителя, то нужно покрасить e и родительское ребро одновременно. После того, как мы либо покрасили e, либо проигнорировали e, снова находим самое глубокое неокрашенное ребро и повторяем процесс.

Задача F (Шарообмен)

Если ответ для (p, q, r, s) — «Yes», то ответ для (p + 2, q, r, s) — тоже «Yes». Это верно, потому что если выполнить одну и ту же операцию два раза подряд, то ничего не изменится. Интуитивно понятно, что если p достаточно большое, то ответы для (p, q, r, s) и (p + 2, q, r, s) совпадают. На самом деле можно доказать, что если p ≥ 48, то это верно. Используя эти наблюдения, можно предполагать, что p, q и r малы, поэтому можно использовать динамическое программирование для решения задачи (dp[p][q][r][s]: можно ли переделать s в «RGB», используя операции p, q, r раз соответственно?).

Вот формальное доказательство. Построим граф из 48 вершин. Каждая вершина соответствует набору значений: (четность p, четность q, четность r, s). Последовательность операций соответствует пути в этом графе. Если этот путь достаточно длинный, то в нем есть циклы. Если цикл содержит p', q' и r' раз соответсвтующие операции, то эти числа четны, и мы можем удалить цикл и показать, что ответ для (p - p', q - q', r - r', s) — «Yes». Мы можем повторять этот процесс, пока p, q и r не станут не более 48.

Оказывается, можно заменить число 48 на число 3, если поэкспериментировать на компьютере.