mtewathia99's blog

How to solve this problem ? DP ? BIT ? TRIE ?
By mtewathia99, history, 4 years ago, In English

Question :

Given 2 arrays 'A' and 'B' both of size 'N'. Make 'N' pairs ( A[ i ], B[ j ] ) such that :

  1. First element of pair should be from array 'A' and second element from array 'B'. ( we cannot make pair ( A[1], A[3] ) )
  2. An element cannot occur in more than one pair. { i.e for every 2 pairs ( A[i], B[j] ) , ( A[k], B[l] ) (i != k and j != l) }
  3. Let the value of a pair be the XOR of first and second element of the pair, value of all the pairs formed must be equal.

Constraints : 0 <= A[i], B[i] <= 10^9 __________ ( 1 <= i <= N )

( Consider N even as the problem can be solved for odd N in O(N) easily )

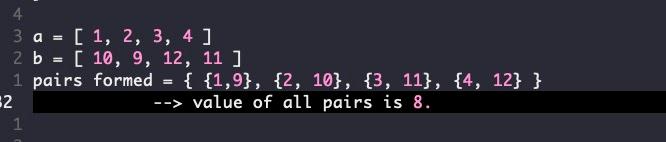
How to solve it in less than O(N^2) Time Complexity ?

If not possible return -1

  • Vote: I like it
  • +49
  • Vote: I do not like it

»
4 years ago, # |
  Vote: I like it -6 Vote: I do not like it

Lets try to find x,for ith bit of x let's calculate ith on and off bits in both arrays, if no. of on bits in a is equal to no.of off bits in b, then we can turn ith bit on,else we turn it off.So after finding x, we can easily find pairs by searching a[i]^x in b. Correct me if its wrong.

Sorry for English.

→ Reply
  • »
    »
    4 years ago, # ^ |
    ← Rev. 2   Vote: I like it +2 Vote: I do not like it

    if ith bit in A is set n/2 times and unset n/2 times and in B also ith bit is set n/2 times and unset n/2 times ,so in this case what do we do ? ( Consider n to be even )

    → Reply
»
4 years ago, # |
  Vote: I like it -15 Vote: I do not like it

Nice Question !

→ Reply
»
4 years ago, # |
  Vote: I like it -12 Vote: I do not like it

You fix the element A[0] and then find the set of numbers S = {A[0]^B[i], 1<=i<=N}

I believe you know how it goes from here.

→ Reply
  • »
    »
    4 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Sorry but how is that going to help in getting near to the solution? I mean even if it would that is for sure the first step anyone would try, but what to do next is I suppose what most of us want to know.

    Can u kindly explain further steps in a bit more detail?

    → Reply
    • »
      »
      »
      4 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Let the value of a pair in a correct solution (if it exists) be k then k is in S.

      Since A[0] must be xored with some B[i] to get k, right?

      For each element e in S, we calculate the multiset B' = {A[i]^e, 1<=i<=N} and then check if this multiset has the same content as the array B. If B' is the same as B then we found the value k.

      If there is no e in S that would produce B'=B output -1.

      Hope this is clear enough :)

      → Reply
      • »
        »
        »
        »
        4 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Isn't it O(N^2), if try for every k ?

        → Reply
        • »
          »
          »
          »
          »
          4 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          Oh less than O(N^2). Now I see it. My bad.

          → Reply
»
4 years ago, # |
  Vote: I like it 0 Vote: I do not like it

As VoidHead said, we can try to find x, using divide and conquer method. I cannot prove the correctness of the algorithm, but my solution works correctly on random tests.

Solution
→ Reply
  • »
    »
    4 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Yes we can solve it this way but the question remains the same can we solve it in less than O(N^2) ?

    As you are making 4 recursive calls every time, Please explain the time complexity of your solution .

    → Reply
    • »
      »
      »
      4 years ago, # ^ |
        Vote: I like it +3 Vote: I do not like it

      Yes, I think I was wrong. This solution works O (N ^ 2).

      → Reply
»
4 years ago, # |
← Rev. 3   Vote: I like it 0 Vote: I do not like it

Auto comment: topic has been updated by mtewathia99 (previous revision, new revision, compare).

→ Reply
»
4 years ago, # |
  Vote: I like it 0 Vote: I do not like it

What's the O(n) solution for odd n?

→ Reply
  • »
    »
    4 years ago, # ^ |
      Vote: I like it +13 Vote: I do not like it

    Xor of each pair will be equal to xor of all numbers in A and B if N is odd.

    → Reply
    • »
      »
      »
      4 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      ah, ofc

      → Reply
    • »
      »
      »
      4 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      How ?

      → Reply
      • »
        »
        »
        »
        4 years ago, # ^ |
          Vote: I like it +5 Vote: I do not like it

        Let A = {x1, x2, x3}, B = {y1, y2, y3}

        Suppose we made pairs z1 = {x1, y1}, z2 = {x2, y2}, z3 = {x3, y3}

        We know, value of z1 = x1^y1, z2 = x2^y2, z3 = x3^y3

        Now z1^z2^z3 = x1^y1^x2^y2^x3^y3

        As we know XOR is associative

        z1^z2^z3 = x1^x2^x3^y1^y2^y3

        From the question we also know z1 = z2 = z3 and we also know that XOR of equal values is zero, so

        z1^z2^z3 = z1 = z2 = z3 = x1^x2^x3^y1^y2^y3.

        → Reply