Задача А. В условии пропущен (UPD: добавлен) пункт, что стороны плитки должны быть параллельны сторонам площади. Это условие делает задачу тривиальной: координаты разделяются, и ответ равен произведению количества плиток, необходимых для закрытия по вертикали, на количество плиток, необходимых по горизонтали.
т.е. answer = ceil (m/a) * ceil (n/a)
где ceil - наименьшее целое, большее или равное аргументу. В целых числах обычно ceil(a/b) заменяется на ((a+b-1)/b) -- внешние скобки нужны для задания порядка операций.
Неприятности в этой задаче заключались в основном с типизацией и приоритетом вычислений, что очень сильно зависит от стиля кодирования и языка.
Задача B.
Отождестим буквенную запись столбца с числом в системе счисления с основанием 26. ('A' = 0, 'B'=1, 'Z' = 25). Тогда при переводе из буквенного обозначения в цифровое нужно к значению дополнительно добавить количество всех вариантов, имеющих меньшую длину, плюс один (ради формализма можно считать, что вариантов нулевой длины -- один, и отказаться от добавления единицы).
При переводе из цифрового обозначения в буквенное нужно сначала найти, сколько знаков понадобится и из числа вычесть количество обозначений меньшей длины (для чего последовательно вычитаем из числа количество обозначений, имеющих длину 0, потом количество имеющих длину 1, 2, и т.п., пока число не станет меньше, чем количество обозначений, имеющих текущую длину и следующее вычитание привело бы к появлению отрицательного числа), переводим в систему счисления 'A'..'Z'.
Возможна интерпретация, реализуемая более компактно, но там сложнее не допустить ошибку при реализации.
Задача C.
Можно разбить на две подзадачи: найти центр правильного многоугольника и найти число углов.
Центр многоугольника обязан быть на одинаковом расстоянии от трех вершин. Можно воспользоваться обычным методом нахождения центра окружности, построенной по трем точкам. Напишу метод, которым воспользовался я. Для двух отрезков (x1,y1 - x2,y2) , (x2,y2 - x3,y3) находим среднюю точку, строим перпендикуляры, пересечение их даст искомый центр. Из подводные камни здесь: некоторые формулы в некоторых частных случаях дают деление на ноль. Лежать на одной прямой три точки из условия не могут (т.к. гарантируется корректность входных данных), а оставшийся плохой случаи можно устранить поворотом всей системы (т.е. всех трех точек) на случайно выбранный угол.
Нахождение числа углов
Поскольку при равном расстоянии от центра до вершины площадь правильного многоугольника возрастает монотонно с ростом N, можно просто перебирать все N, начиная с 3, и при нахождении первого подходящего печатать ответ и прекращать работу. Нужно, следовательно, для данного N уметь определять, могут ли данные вершины быть вершинами N-угольника -- критерий прост: углы между отрезками от центра до вершин должны быть кратны 2*pi/N. Воспользуемся свойством синуса: sin(x)=0, если аргумент кратен пи. Условие кратности угла между двумя отрезками заменяется при этом на следующее:
sin( N * (a[i]-a[j]) /2 )=0
т.к. имеем дело с арифметикой конечной точности, то:
fabs( sin( N * (a[i]-a[j]) /2 ) ) < eps
a[i] посчитаем просто: atan2( y[i] - ycenter, x[i] - xcenter)
[/cut]











Вместо описанной конструкции (a+b-1)/b для нахождения ответа я использовал куда более очевидную (на мой взгляд) , но более длиную конструкцию:
long res = a/b;
if (a%b>0){
res++;
}
Ваш вариант тоже приму на заметку. Спасибо за разбор.
double gcd(double x, double y) { if (fabs(y) < EPS) return x; return gcd(y, fmod(x, y)); }по-моему тут опечатка) должно быть примерно так:
ceil(x) - наименьшее целое, не меньше x.
It is conventional to use positional systems where the least digit means zero, not one -- it is more logically consistent.
I do not understand your reference to 64/65 at all.
Ah, I see. This is technical issue, dependant on language being used. BTW, here, 65 is magical number (which should be avoided).
Я искал центр описанной окружности двумя вложенными тернарными поисками.
fabs( sin( N * (a[i]-a[j]) /2 ) ) < eps
а сколько лучше взять eps?
frac{x}{y} = 3
for example.
$$$\frac{x}{y}$$$ = 4
I can't pass Test case 6.
I don't konw why? Isn't there a test case like:
Input: R001C001
Ouput: 00A001
?
A001
No leading zeros needed. "A1" is correct.
It is "RZ288".
You cannot have zeros in letter numbering. "00A" is incorrect, it should be only "A". "001" is not incorrect, but the leading zeros are unnecessary, it can be simply "1". I doubt though that there are numbers with leading zeros in the official test cases, it is simply "R1C1" or "A1".
Спасибо за разбор. Добавлю свои 5 копеек, надеюсь, что помогут кому-нибудь.
В задаче B не думал про системы счисления, а реализовывал восстановление размещения по номеру. В этом случае даже о количестве символов задумываться не приходится, все само собой получается (хотя это само собой получается). То есть количество символов при переводе можно не считать, это упрощение.
А вот по задаче С могу немного больше сказать. Действительно, центр можно не искать, ведь радиус мы можем найти из данных трех точек как окружности, описанной вокруг треугольника (действительно, если точки треугольника лежат на многоугольнике, то их описанные окружности совпадают). R = abc/4S. Площадь находится из векторного произведения. Тут в разборе предлагалось искать какие-то тангенсы и про какие-то деления на 0 говорилось, но можно без этого. Нам даны три хорды и если мы соединим концы хорды с центром, то получим равнобедренный треугольник. И у нас 3 таких треугольника и углы (из центра) нам нужно проверить, что кратны 2pi/n. Поскольку угол может быть тупой, то синус не знает как себя вести, поэтому можно схитрить и поделить этот угол на 2. И тогда все снова немного упростится, а синус этого половинного угла можно легко найти как d/2r, где d - противолежащая хорда. Не примите за хвастовство, но реализацию этого на С++ можете найти в списке решений этой задачи, если упорядочите их по размеру кода: первое решение.
Вот, надеюсь, что кому-то это пригодится :)
try to check this test instead:
13
R1C17
R1C18
R1C19
R1C20
R1C21
R1C22
R1C23
R1C24
R1C25
R1C26
R1C27
R1C28
R1C29
after passing this I got AC.
My program that got AC says "R288C494".
This is correct.
B: what about "R1C204152" answer:"KOYZ169801"
That is incorrect. The correct answer is "KOYZ1". The cell is obviously in row 1.
So what?
When I use ceil((float)N/A) for problem 1A, it gives wrong answer while it gives a correct answer when I use ((N+A-1)/A). What is the catch behind it?
Use double, Luke
float has very low precision. Best stay away from it, use double.
Hello :) How do I represent 10^9 integers and input integers separated by space in a single line in C language?
For integers up to 10^9, you can use the 32-bit integral type long int. But if you multiply them, you have to use a 64-bit type, like long long int, otherwise the multiplication will overflow.
As for input, the proper way to input a 32-bit integer on Codeforces is
scanf ("%ld", & integer);
and for a 64-bit integer
scanf ("%I64d", & integer);
Can someone help me in problem 1B ? 1B - Spreadsheet
except this one "R1C204152" answer:"KOYZ169801", all the test cases which users gave in comments run on my machine. Help me please
The correct answer to the test case "R1C204152" is "KOYZ1". The cell is obviously in row 1. I got AC on this problem today.
Okay I mended my one as well to get KOYZ1 but still it fails test 6. Wanna see my code ?
Yes, please.
I have been trying 1B. But getting Runtime error. Here other people also have said same but no reason mentioned. Please suggest me what's wrong.
Try this cell: R1
Problem B. My submission: here WA on test 6, but I can't trace this big test case. Can anyone help me with a one that can be traced and hacks my code? Thanks in advance.
Have you scrolled to the bottom of the submission report?
Не могу понять в чем ошибка седьмого теста задания В (
И еще, в этом же задании, если компилировать код так:
num получит ожидаемое значение 52, если последнюю строку записать иначе, поменяв лишь местами функцию и выражение в скобках:
в результате получаю 51 ??? О_о
С этим я так и не разобрался т.к. по другому ведь работает, но это ведь не вариант. На моем компе работают оба варианта, не работает только на сервисе. Ubutu Linux x86_64, g++ (Ubuntu 4.9.2-10ubuntu13) 4.9.2
У вас в вычислении длины ответа была нестыковка:
В первом цикле вы просто делили num на ALPHACOUNT,
а во втором добавили корректировку числа по нулевому остатку:
Если перенести логику переходов в цикл вычисления длины, то получаем верное решение:
Насчет использования pow — это все-таки вещественная функция, поэтому при приведении к целочисленному типу вы могли получить что-то наподобие (int)51.999999999 -> 51, а в другом случае (int)52.00000001 -> 52. Используйте лучше целочисленное возведение в степень, например:
P.S. У вас некорректно переводился тест R127686C474738 (можно открыть свою посылку и в информации к тесту увидеть данное сообщение):
wrong answer 3223rd words differ — expected: 'ZZGD127686', found: '(ZZGD127686'
I can't solve problem A, please help me. I was using a 2D-Segment Tree to simulate the squares, but I got WA. I need help. If you help me, I'll give you a big hug.
Tip: Solve the problem first in one dimension. Look for an analytical solution of the problem, no advanced data structures are needed.
Please help: Why I'm getting a different output on different systems for Problem B sample test cases?
On my system:
On CF system: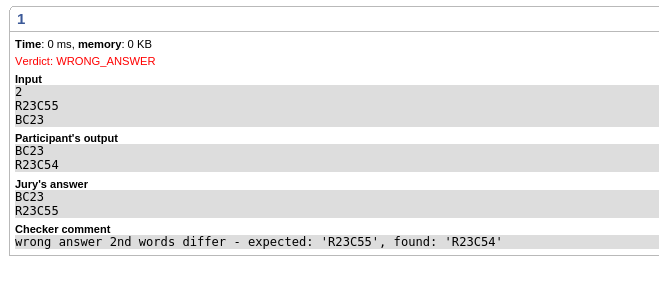
My submission: 16392041
pow pow pow... How many bugs with it. Write your own function.
Did you get correct result .me also facing same problem.
what datatype can i use to this big number in java? numbre: 1000000000000000000
Long.
i try to multiplicate 1000000000X1000000000 and i want that the result was 10000000000000000000, but when i try do this operation in java, the answer of the multiplication give me how result this number -1486618624 whit datatype long and int and BigInteger.
You have to store 1000000000 in a long also, if you want to make operations on it which makes it become a long. You can cast it meanwhile operation too, so you can do ((long) 10000000000)*10000000000, and it will give correct result.
Long can handle numbers up to 9*10^18, for numbers bigger than that you need to use BigInteger.
I found another solution for B here is my code: 33646284
can someone help me with the concept of epsilon in finding the gcd. Why do most of the accepted answers have it as 10^-4 . when i reduce it to 10^-5 , i get incorrect answer. Can someone tell me how did we decide this value because i think that lesser the value of eps meant a more precise answer??
can anyone explain me why my code is not passing testcase 6. https://mirror.codeforces.com/contest/1/submission/58648097
it was a nice contest....it was a og.
hi