Tutorial
Tutorial is loading...
Solution 1
#include <bits/stdc++.h>
using namespace std;
void solve() {
int n;
scanf("%d", &n);
vector <int> in(n);
vector <int> is(N);
for(auto &p: in)
scanf("%d", &p);
for(int i = 0; i < n; ++i)
for(int j = i + 1; j < n; ++j)
is[in[j] - in[i]] = true;
int ans = 0;
for(auto &v: is)
ans += v;
printf("%d\n", ans);
}
int main() {
int cases;
scanf("%d", &cases);
while(cases--)
solve();
return 0;
}
Solution 2
#include <bits/stdc++.h>
using namespace std;
void solve() {
int n;
scanf("%d", &n);
vector <int> in(n);
for(auto &p: in)
scanf("%d", &p);
set <int> S;
for(int i = 0; i < n; ++i)
for(int j = i + 1; j < n; ++j)
S.insert(in[j] - in[i]);
printf("%d\n", (int)S.size());
}
int main() {
int cases;
scanf("%d", &cases);
while(cases--)
solve();
return 0;
}
Challenge
Try to solve it for $$$n, x_i \leq 10^5$$$.
1466B - Last minute enhancements
Tutorial
Tutorial is loading...
Solution 1
#include <bits/stdc++.h>
using namespace std;
void solve() {
int n;
scanf("%d", &n);
int ans = 0;
int prv = 0, ok = 0;
for(int i = 1; i <= n; ++i) {
int a;
scanf("%d", &a);
ans += (a != prv);
ok |= (a == prv);
if(prv + 1 < a)
ans += ok, ok = 0;
prv = a;
}
ans += ok;
printf("%d\n", ans);
}
int main() {
int cases;
scanf("%d", &cases);
while(cases--)
solve();
return 0;
}
Solution 2
#include <bits/stdc++.h>
using namespace std;
void solve() {
int n;
scanf("%d", &n);
set <int> S;
for(int i = 1; i <= n; ++i) {
int v;
scanf("%d", &v);
if(S.count(v))
v++;
S.insert(v);
}
printf("%d\n", (int)S.size());
}
int main() {
int cases;
scanf("%d", &cases);
while(cases--)
solve();
return 0;
}
Challenge
Can you solve it if we can increase note $$$x_i$$$ by any integer in $$$[0, k_i]$$$, for given $$$k_i$$$?
- Author: Okrut
- Developer: Anadi
- First solve: thenymphsofdelphi
Tutorial
Tutorial is loading...
Solution 1
#include <bits/stdc++.h>
using namespace std;
const int N = 100 * 1000 + 7;
int n;
char in[N];
bool used[N];
void solve(){
scanf("%s", in + 1);
n = strlen(in + 1);
for(int i = 1; i <= n; ++i)
used[i] = false;
int ans = 0;
for(int i = 2; i <= n; ++i){
bool use_need = false;
if(in[i] == in[i - 1] && !used[i - 1])
use_need = true;
if(i > 2 && in[i] == in[i - 2] && !used[i - 2])
use_need = true;
used[i] = use_need;
ans += used[i];
}
printf("%d\n", ans);
}
int main(){
int cases;
scanf("%d", &cases);
while(cases--)
solve();
return 0;
}
Solution 2
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 7;
int n;
char in[N];
int dp[N][2][2];
void solve(){
scanf("%s", in + 1);
n = strlen(in + 1);
for(int ta = 0; ta < 2; ++ta)
for(int tb = 0; tb < 2; ++tb)
dp[0][ta][tb] = 0;
for(int i = 1; i <= n; ++i)
for(int ta = 0; ta < 2; ++ta)
for(int tb = 0; tb < 2; ++tb)
dp[i][ta][tb] = N;
for(int i = 1; i <= n; ++i){
if(in[i] != in[i - 1]){
if(in[i] != in[i - 2])
dp[i][0][0] = min(dp[i][0][0], dp[i - 1][0][0]);
dp[i][0][0] = min(dp[i][0][0], dp[i - 1][0][1]);
}
if(in[i] != in[i - 2])
dp[i][0][1] = min(dp[i][0][1], dp[i - 1][1][0]);
dp[i][0][1] = min(dp[i][0][1], dp[i - 1][1][1]);
dp[i][1][0] = min(dp[i][1][0], min(dp[i - 1][0][0], dp[i - 1][0][1]) + 1);
dp[i][1][1] = min(dp[i][1][1], min(dp[i - 1][1][0], dp[i - 1][1][1]) + 1);
}
int ans = N;
for(int ta = 0; ta < 2; ++ta)
for(int tb = 0; tb < 2; ++tb)
ans = min(ans, dp[n][ta][tb]);
printf("%d\n", ans);
}
int main(){
int cases;
scanf("%d", &cases);
while(cases--)
solve();
return 0;
}
Challenge
What if letters can change, and you need the calculate the result after each change?
1466D - 13th Labour of Heracles
Tutorial
Tutorial is loading...
Solution
#include <bits/stdc++.h>
using namespace std;
typedef long long int LL;
const int N = 100 * 1000 + 7;
int n;
int w[N];
int deg[N];
void solve() {
scanf("%d", &n);
for(int i = 1; i <= n; ++i) {
scanf("%d", &w[i]);
deg[i] = 0;
}
for(int i = 1; i < n; ++i) {
int u, v;
scanf("%d %d", &u, &v);
deg[u]++; deg[v]++;
}
LL ans = 0;
vector <int> to_sort;
for(int i = 1; i <= n; ++i) {
for(int j = 1; j < deg[i]; ++j)
to_sort.push_back(w[i]);
ans += w[i];
}
sort(to_sort.begin(), to_sort.end());
reverse(to_sort.begin(), to_sort.end());
for(auto &v: to_sort) {
printf("%lld ", ans);
ans += v;
}
printf("%lld\n", ans);
}
int main() {
int cases;
scanf("%d", &cases);
while(cases--)
solve();
return 0;
}
- Author: Okrut
- Developer: Anadi
- First solve: dengyipeng
Tutorial
Tutorial is loading...
Solution
#include <bits/stdc++.h>
using namespace std;
typedef long long int LL;
const int N = 500 * 1000 + 7;
const int P = 60;
const int MX = 1e9 + 7;
int n;
LL in[N];
int cnt[P];
void solve(){
scanf("%d", &n);
for(int i = 0; i < P; ++i)
cnt[i] = 0;
for(int i = 1; i <= n; ++i){
scanf("%lld", &in[i]);
for(int j = 0; j < P; ++j)
cnt[j] += in[i] >> j & 1;
}
int ans = 0;
for(int i = 1; i <= n; ++i){
LL exp_or = 0, exp_and = 0;
for(int j = 0; j < P; ++j){
if(in[i] >> j & 1){
exp_or += (1LL << j) % MX * n;
exp_and += (1LL << j) % MX * cnt[j];
}
else
exp_or += (1LL << j) % MX * cnt[j];
}
exp_and %= MX, exp_or %= MX;
ans = (ans + 1LL * exp_or * exp_and) % MX;
}
printf("%d\n", ans);
}
int main(){
int cases;
scanf("%d", &cases);
while(cases--)
solve();
return 0;
}
Tutorial
Tutorial is loading...
Solution
#include <bits/stdc++.h>
using namespace std;
typedef long long int LL;
const int N = 5e5 + 7;
const int MX = 1e9 + 7;
int n, m;
int rep[N];
int Find(int a) {
if(rep[a] == a)
return a;
return rep[a] = Find(rep[a]);
}
bool Union(int a, int b) {
a = Find(a);
b = Find(b);
rep[a] = b;
return a != b;
}
int main() {
scanf("%d %d", &n, &m);
for(int i = 1; i <= m + 1; ++i)
rep[i] = i;
vector <int> ans;
for(int i = 1; i <= n; ++i) {
int k;
scanf("%d", &k);
int fa, fb = m + 1;
scanf("%d", &fa);
if(k > 1)
scanf("%d", &fb);
if(Union(fa, fb))
ans.push_back(i);
}
int res = 1;
for(int i = 0; i < (int)ans.size(); ++i)
res = (res + res) % MX;
printf("%d %d\n", res, (int)ans.size());
for(auto v: ans)
printf("%d ", v);
puts("");
return 0;
}
Tutorial
Tutorial is loading...
Solution
#include <bits/stdc++.h>
using namespace std;
const int MAXLEN = 1e6 + 7;
const int MOD = 1e9 + 7;
int n, q;
string s, t;
vector <string> songs;
vector <int> pw;
vector <int> sum[26];
void read(string &p) {
static char input[MAXLEN];
scanf("%s", input);
p = input;
}
void prepare_songs() {
songs = {s};
for(auto c: t) {
if(songs.back().size() >= MAXLEN)
break;
auto p = songs.back();
auto nxt = p + string(1, c) + p;
songs.push_back(nxt);
}
}
void prepare_sum() {
for(int i = 0; i < 26; ++i) {
char c = 'a' + i;
sum[i].resize(n + 1, 0);
for(int j = 0; j < n; ++j)
sum[i][j + 1] = (sum[i][j] * 2 + (t[j] == c)) % MOD;
}
pw.resize(n + 1, 0);
pw[0] = 1;
for(int i = 1; i <= n; ++i)
pw[i] = 2LL * pw[i - 1] % MOD;
}
void init() {
scanf("%d %d", &n, &q);
read(s), read(t);
prepare_songs();
prepare_sum();
}
vector <int> kmp(string &in) {
int m = in.size(), cpref = 0;
vector <int> dp(m, 0);
for(int i = 1; i < (int)in.size(); ++i) {
while(cpref > 0 && in[cpref] != in[i])
cpref = dp[cpref - 1];
if(in[cpref] == in[i])
++cpref;
dp[i] = cpref;
}
return dp;
}
/* Get all borders based on dp from kmp */
vector <bool> get(vector <int> &dp, int m) {
vector <bool> ret(m + 1, false);
int cur = dp.back();
while(cur) {
ret[cur] = true;
cur = dp[cur - 1];
}
ret[cur] = true;
return ret;
}
int answer(int k, string &w) {
int id = 0;
while(songs[id].size() < w.size())
++id;
if(id > k)
return 0;
int m = w.size();
string s_pref = w + '#' + songs[id];
string s_suf = songs[id] + '#' + w;
auto dp_pref = kmp(s_pref);
auto dp_suf = kmp(s_suf);
auto pref = get(dp_pref, m);
auto suf = get(dp_suf, m);
/* Compute all internal occurences */
int ret = 0;
for(auto &v: dp_pref)
ret += (v == m);
ret = 1LL * ret * pw[k - id] % MOD;
/* Compute the remaining occurences */
for(int i = 0; i < m; ++i) {
if(!pref[i] || !suf[m - i - 1])
continue;
int c = w[i] - 'a';
ret = (ret + sum[c][k] - 1LL * sum[c][id] * pw[k - id]) % MOD;
}
ret = (ret + MOD) % MOD;
return ret;
}
void solve() {
while(q--) {
int k;
string w;
scanf("%d", &k);
read(w);
printf("%d\n", answer(k, w));
}
}
int main() {
init();
solve();
return 0;
}
1466H - Finding satisfactory solutions
Tutorial
Tutorial is loading...
Solution
#include <bits/stdc++.h>
using namespace std;
typedef long long int LL;
#define st first
#define nd second
#define PII pair <int, int>
const int N = 60;
const int MX = 1e9 + 7;
struct state {
int sum_picked = 0;
int last_picked = 0, cur_picked = 0;
int iterator = 0;
vector <PII> lengths;
state(vector <PII> _lengths) {
lengths = _lengths;
}
/* operators for map comparisons */
bool operator<(const state &s) const {
if(lengths != s.lengths) return lengths < s.lengths;
if(last_picked != s.last_picked) return last_picked < s.last_picked;
if(cur_picked != s.cur_picked) return cur_picked < s.cur_picked;
return iterator < s.iterator;
}
bool operator==(const state &s) const {
if(last_picked != s.last_picked) return false;
if(cur_picked != s.cur_picked) return false;
if(iterator != s.iterator) return false;
if(lengths != s.lengths) return false;
return true;
}
};
int n;
vector <PII> cycles;
map <state, int> dp;
int sil[N], rv[N];
int pre[N][N][N];
int fast(int a, int b) {
int ret = 1;
while(b) {
if(b & 1)
ret = 1LL * ret * a % MX;
b >>= 1;
a = 1LL * a * a % MX;
}
return ret;
}
int newt(int a, int b) {
if(b < 0 || a < b)
return 0;
return 1LL * sil[a] * rv[b] % MX * rv[a - b] % MX;
}
PII get_ways(int a, int b) {
if(a == 0 && b == 0)
return {sil[n - 1], 0};
int ret = 0, ret2 = 0;
int c = n - a - 1;
for(int t = 1; t + c <= n; ++t) {
ret = (ret + 1LL * newt(n - t, c) * sil[c] % MX * newt(n - c - 1, b) % MX * sil[b] % MX * sil[a - b]) % MX;
ret2 = (ret2 + 1LL * newt(n - t, c) * sil[c] % MX * newt(n - t - c, b) % MX * sil[b] % MX * sil[a - b]) % MX;
}
return {ret, ret2};
}
void precalc() {
sil[0] = 1;
for(int i = 1; i <= n; ++i)
sil[i] = 1LL * sil[i - 1] * i % MX;
rv[n] = fast(sil[n], MX - 2);
for(int i = n; i >= 1; --i)
rv[i - 1] = 1LL * rv[i] * i % MX;
for(int i = 0; i < n; ++i)
for(int j = 0; j <= i; ++j) {
if(i && j == 0)
continue;
auto [val, val2] = get_ways(i, j);
pre[i][j][0] = 1;
int res = 1, res2 = 1;
for(int k = 1; k <= n; ++k) {
res = 1LL * res * val % MX;
res2 = 1LL * res2 * val2 % MX;
pre[i][j][k] = (res + MX - res2) % MX;
}
}
}
void read() {
scanf("%d", &n);
precalc();
vector <int> input(n);
for(auto &v: input) {
scanf("%d", &v);
v--;
}
vector <bool> vis(n);
vector <int> cycle_lengths;
for(int i = 0; i < n; ++i) {
if(vis[i])
continue;
int cur = i;
int cycle_length = 0;
while(!vis[cur]) {
++cycle_length;
vis[cur] = true;
cur = input[cur];
}
cycle_lengths.push_back(cycle_length);
}
sort(cycle_lengths.begin(), cycle_lengths.end());
for(auto v: cycle_lengths) {
if(cycles.size() && cycles.back().st == v)
cycles.back().nd++;
else
cycles.push_back({v, 1});
}
}
int solve(state &cur) {
if(cur.sum_picked == n)
return 1;
if(dp.count(cur))
return dp[cur];
if(cur.iterator == (int)cur.lengths.size()) {
if(cur.cur_picked == 0)
return dp[cur] = 0;
state nxt = cur;
nxt.sum_picked += nxt.cur_picked;
nxt.last_picked = nxt.cur_picked;
nxt.cur_picked = 0;
nxt.iterator = 0;
return dp[cur] = solve(nxt);
}
state nxt = cur;
nxt.iterator++;
int ret = 0, tmp = 1;
auto [length, count] = cur.lengths[cur.iterator];
for(int i = 0; i <= count; ++i) {
nxt.cur_picked = cur.cur_picked + i * length;
nxt.lengths[cur.iterator].nd = count - i;
ret = (ret + 1LL * solve(nxt) * tmp % MX * newt(count, i)) % MX;
tmp = 1LL * tmp * pre[cur.sum_picked][cur.last_picked][length] % MX;
}
return dp[cur] = ret;
}
int main() {
read();
state start = state(cycles);
int ans = solve(start);
printf("%d\n", ans);
return 0;
}
1466I - The Riddle of the Sphinx
- Authors: gawry, Anadi
- Developer: Anadi
- First solve: fivedemands
Tutorial
Tutorial is loading...
Solution
#include <bits/stdc++.h>
using namespace std;
#define st first
#define nd second
int n, b;
void write(int i, string y){
printf("%d ", i);
for(auto p: y)
printf("%c", p);
puts("");
fflush(stdout);
}
bool ask(int i, string y){
write(i, y);
string ans;
cin >> ans;
return ans == "yes";
}
void solve(vector <int> cur, string pref){
if(pref.size() == b){
write(0, pref);
return;
}
stack <pair <int, string> > S;
S.push({0, pref});
for(auto v: cur){
while(S.size() > 1){
auto prv = S.top().nd;
while(prv.size() < b)
prv.push_back('1');
if(!ask(v, prv))
break;
S.pop();
}
if(S.top().nd.size() == b)
continue;
auto prv = S.top().nd;
prv.push_back('0');
while(prv.size() < b)
prv.push_back('1');
if(ask(v, prv)){
prv = S.top().nd + "1";
S.push({v, prv});
}
else{
prv = S.top().nd + "0";
S.push({v, prv});
}
}
vector <int> nxt;
string ans = S.top().nd;
while(S.size() > 1){
auto p = S.top();
S.pop();
string tmp = ans;
while(tmp.size() < b)
tmp.push_back('1');
if(ask(p.st, tmp)){
nxt.clear();
ans = p.nd;
}
nxt.push_back(p.st);
}
solve(nxt, ans);
}
int main(){
scanf("%d %d", &n, &b);
vector <int> all_ids;
for(int i = 0; i < n; ++i)
all_ids.push_back(i + 1);
solve(all_ids, "");
return 0;
}
I am really interested in solving this task using fewer queries or proving that $$$3 \cdot (n + b)$$$ is optimal. Does anyone have any idea how to answer these questions?
UPD: There are challenges added to some tasks.










Thanks for the fast editorial! Loved the round btw. :)
Happy New Year)
Happy New year :)
some telegram pages leak solution please check plagiarism
Ending 2020 on a high note, really awesome problems!
B was bit tricky. Nice problemset though and fast editorial
B was a bit tricky. Nice problemset though and fast editorial.
Surely commenting 2 times the same thing doesn't give double the no. of upvotes. XD (It was unintentional, some net issue)
three times does.
A nice round to end the year :)
Happy New Year! Nice contest to end this year
My $$$O(60*N)$$$ Java solution for E got TLE 2 Sec was a tight limit
Limits were tight for Java. 26*26*N solution for C doesn't pass :(
A trick for the future:
If you're adding a + b and (a < mod and b < mod), then (a+b) % mod is equivalent to
Given the slow nature of mod and java this will really help you squeeze under time limit
You forgot to include the equality too i guess if(c>=mod)
Am i wrong?
never mind you are correct
isn't it
if(c >= mod) c -= mod?Wow, I discovered exactly the same bug in my Modular class in library, which I was (successfully!!!) using during around 1.5 years and around 20 AC submits...
Thank you so much!!!
Hope 2021 is not the same as 2020 : ) Happy New Year!
There are two sides to that, which do you mean?
CODE why is this getting RE ?
Amazing problems as well as amazing editorials. Kudos to the setter :))
A very good problem set loved it!
It's probably $$$\mathcal{O}(n + q \cdot | \Sigma | + S)$$$ in G. Or it's possible to completely get rid of the alphabet size?
If you solve it offline, it is possible to solve it in linear time (assuming that the alphabet is $$$\mathcal{O}(n)$$$).
Ah yeah, it's kinda contained in $$$S$$$ part. Isn't it possible to solve it online: SA for occurrences in the short parts and KMP for the long parts? The only problem is the prefix sums cuz we get an extra $$$\log n$$$ don't see how "offline-ness" helps in any way.
I was thinking about something like having for each letter memorized its value (prefix sum) and last occurrence. I think it should be enough to recover the answer in $$$\mathcal{O}(1)$$$ for a fixed letter.
Nice problem set, but problem statements were not short (which is not cool).
They weren't long either? Just enough length to make it have fun theme I thought.
fun theme. But I feel like I went through an difficult English test XD.
I felt the same haha
I think the statements were just right. One could skip reading the story and other embellishments fairly easily. I personally enjoyed reading the story part; Makes the problem not-so-forgettable. Though, this is just my opinion.
yeah, it's a little hard for me to understand the statement, maybe my English is so pool.
yeah, a bit pool
In solution 1 of problem A, N is not defined.
If anyone has some alternate approach for C ..then share ..Tx in advance
This one passed the pretests (for now) and is not a dp solution but what i basically thought was that the palindrome of length 2 or 3 should not exist, so basically
s[i] != s[i+1] || s[i] != s[i+2]If it does happen then I change the values of
s[i+1]ors[i+2]to#sign. The reason being that im considering#to hold a value that is not equal to its i+2 or i+1. So if i ever encounter#sign i skip it knowing that ifs[j] = #then theres no need to checks[j+1] || s[j+2]because it will not be ever equal. Hence the answer is just the number of#signs in the resulting string! Code (I used # here because the dollar sign was converting my text to latex)Good bye, orange :'(
For problem E, even in C++, my O(60*N) solution got TLE, what could be the reason my solution
A lot of %mod and fastio is missing. Not sure.
Probably fast io, I did something similar with fastio and got 1500ms and then resubmitted with c++17(64bit) by precomputing powers of 2 by mod and got 500ms
Will a solution which got accepted in g++ 17 will also get accepted in 64 bit always ? I might be wrong but in initial days (when 64 bit was launched) i got WA but same got accepted in g++ 17.
tbh thats the same reason I stopped using 64 bit back then, one of the contests it gave wa whereas the same code gave ac in g++14 or 17. Now I only use 64bit for problems with tight TL since its twice as fast if using along long long.
If anyone knows the reason to this please reply
Jus precalculate all powers of 2 modulo 1e9+7. But don't use them for bitwise operations. Use left shift operator for them.
My O(60*N) solution failed too :( I guess fastio will help
You are reading around $$$500\,000$$$ numbers with
cinwithoutios_base::sync_with_stdio(false).I hoped for an explanation what 1466F - Euclid's nightmare asks for, and how we can interpret the input. What is the meaning ok k? (that value that is 1 or 2)
It tells number of positions in the vector where 1 is present . maximum number of 1 in the vector can be 2 . For example in 1100000 , k=2 . Isn't that obvious from samples ?
For me it is not obvious, no. Why is the maximum number of 1s in the vector 2. Is this by definition, or is this some basic property of the vectors?
ok . It was mentioned in the question that "at most 2 coordinates equal 1" . Thus it was defined in the question , it's not property of vectors .
There is a defintion of "Consider sets A and B such that..." What is this good for? I cant relate that to the other parts of the statement.
For explaining "lexicographically smaller" .You need to output lexicographically smallest subset in case of same size.
O($$$n$$$ * 26 2 ) dp gave MLE in problem $$$C$$$.
but
that's a nice observation, i wish i had observed it.
It actually shouldn't you have an extra dimension of length in your dp array in the way you have implemented it, just make it dp[26][26]. Here is my iterative O(n*(26^2)) dp 102865773.
Can someone explain me how to solve F?
PS: I am newbie in Linear Algebra.
My solution to 1466F - Euclid's nightmare
We can use DSU to solve this problem in one pass. A key point here is to create a virtual node $$$m$$$ (we use 0-index here, so we have $$$0\dots m-1$$$ as actual nodes) and connect all single nodes to it.
For each vector:
Now that we already have $$$|S'|$$$ and the final selection, we need to calculate $$$T$$$, which is actually as simple as:
Where $$$size[i]$$$ means the size of the $$$i$$$-th connected component.
The time complexity is thus $$$\mathcal{O}(n+m)$$$ (here we neglect the $$$\alpha(n)$$$ part).
Explanation:
Thanks a lot for the explanation of T calculation. I didn't understand from editorial why it should be 2^{s'}.
My thought is that for each vector in the answer, you can either use or not use it, so this gives $$$2^{|S'|}$$$
In a very similar idea (maybe same idea), you can just use path compression and run the algorithm that generates a xor basis that is in this blog. Basically we have n vector's with at most 2 active bits and $$$f(\vec{v_i}) = min(x_1, x_2)$$$ (or just $$$x_1$$$ if $$$k = 1$$$) where $$$f(\vec{v_i})$$$ is simply the first active bit of the vector $$$i$$$ and $$$f_2(\vec{v_i}) = max(x_1, x_2)$$$ (or $$$-1$$$ if $$$k = 1$$$) where $$$f_2(\vec{v_i})$$$ is the second bit active in $$$v_i$$$.
If the basis doesn't contain $$$f(\vec{v_i})$$$, you add this vector to the basis and you create an edge from $$$f(\vec{v_i})$$$ to $$$f_2(\vec{v_i})$$$. What this means is if you arrive at this bit in some point while checking if a vector $$$j$$$ is represented by the basis, it means you will remove $$$f(\vec{v_j})$$$ from it and add $$$f_2(\vec{v_i})$$$ (while doing the operation $$$\vec{v_j} = \vec{v_j} - \vec{v_i}$$$). So to finish it up, you do the same to the second bit of vector $$$j$$$, if you get that they are the same value (or they are equal to $$$-1$$$), it means they cancel eachother out and the vector $$$j$$$ is represented by the basis. Otherwise you have a valid new bit that currently can't be represented by the basis.
The only downside is the complexity which is something like $$$O((n+m)log(m))$$$.
Submission
It's a really good explanation, but can you tell me what do you mean by "since each addition will add either 2 or 0 set bits"?
Suppose we have {1,2}, {2,3}, {3,4}. Obviously, there is no free bit, while all bits are in a connected component.
Starting from {1,2}, if we add {2,3}, then 2 is erased while 3 is added, so set bits remain unchanged. If we add {3,4}, then set bits increase by 2.
Would you consider this case, please?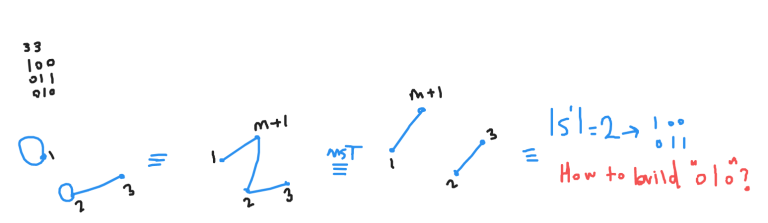
Oh, It's not MST at all! Thanks.
Can you recommend other problems like this one to practice? I still unable to figure out how to reduce this kind of problem to a graph problem and then to DSU or MST. Thanks
I gave my first contest today. attempted the first A level question in python and after the contest, I check my rating it is still zero and in the submission section, it is written queue under verdict, can anyone guide me on what is queue meaning in the submission section, and is it the reason my rating didn't changed?
It needs some time, just be patient.
During the contest your solution was tested only on some tests (called pretests) and now it's waiting to be judged on full testset (and looking at current state of the queue: https://mirror.codeforces.com/contest/1466/status I fear it might wait for a while). After all submissions are judged the final standings will be available, everyone's rating will update several hours later. You can install this plugin: chrome://extensions/?id=ocfloejijfhhkkdmheodbaanephbnfhn (at least in Chrome, idk if there's anything like this for other browsers) to see immediately approximate rating change you will get.
What should I change in this submission to not receive compilation error?
https://mirror.codeforces.com/contest/1466/submission/102855965
The reason is multiset<pi, cmp> will keep some constant object of type cmp and will call operator() on it So instead of this
you should use
this const means the method can be called on a const object
Wow, that's true
Thank you!
Are there any solutions for F which do not require MST?
We can solve it with DSU only. You can refer to my comment above.
If you know about the rank-nullity theorem and that the rank of matrix equals the rank of its transpose, the problem becomes: for each vector with a single non-zero entry $$$u$$$, mark vertex $$$u$$$, otherwise it has another non-zero entry $$$v$$$, so add an edge between $$$u$$$ and $$$v$$$, now count the number of connected components without a marked vertex (this equals the nullity of the $$$n$$$-by-$$$m$$$ matrix with rows equal to the vectors given in the problem). No need to create a virtual vertex.
This solution does not require MST or creating a virtual node which is connected to the 1-bit vectors: https://mirror.codeforces.com/contest/1466/submission/103923589
Disclaimer: code & its comments may be difficult to understand, since I didn't polish any of it for readability.
General idea is that I have a data structure where where you can insert vectors one at a time into it. The data structure can determine whether an inserted vector is redundant with earlier added vectors. It uses ideas from the union-find data structure.
Who else have wasted a lot of time in D? Btw Happy New Year :) .
C can be solved by a greedy approach.
If ith character is same as I — 1 th or I — 2nd, replace by a third character (dummy), increment answer by 1.
Intuition: If any 2 consecutive characters are same, we need to replace one irrespective of other characters.
Is there any solution to solve A in O(n) time ?
Try to solve it for n, xi ≤ 105.
The challenge is supposed to be solved with FFT. So I think there is no $$$\mathcal{O}(n)$$$ solutions.
I believe it is not possible, since it looks very much FFT-like. It is however possible to do it in $$$O(n\log^2(n))$$$ (or even $$$O(n\log(n))$$$, not sure) with D&C + FFT (split in two parts, the distances between different parts are calculated with FFT, the distances in each part are calculated recursively).
UPD. I'm an idiot, it can be done with just one FFT ($$$\sum{x^{x_i}}$$$ and $$$\sum{x^{N - x_i}}$$$)
Hmm, FFT is new to me and I guess for many others.
Is there any source you want to recommend for FFT. Thank you in advance for reply.
lucifer1004, SendThemToHell and others suggestions would be really helpful.
https://cp-algorithms.com/algebra/fft.html
This challenge is very similar to 1398G - Running Competition.
We can do that using data structures like bitset.
Can somebody explain why in problem F doing this trick with increasing m by 1 and assigning m+1-th character to 1 in every vector with k=1 doesn't change the result?
Problem statements were too long and bad. For understanding the problem i need to read notes. At least notes were good.
Can some tell me how to solve the challenge part of Problem A i.e., Try to solve it for n,xi≤10^5
We need to get unique differences, you can do it using bitsets. You need to see what differences you can get. So the solution is -
...Make two bitset of 1e5 + 1 size, call one as present_nums and other as ans .Initally ans and present nums has no set bits. now going from largest to smallest update ans as ans |= (present_nums >> arr[i]) i is the present index. then update present_nums[arr[i]] = 1. Your final ans is set bits in ans. The time complexity is O(n * (n/64)) or O(n * (n/32)). The >> operator is just the set of numbers which you get by subtracting present number with previous small numbers
$$$~$$$
$$$~$$$
$$$~$$$
$$$~$$$
$$$\gets$$$
.
that's why I thought why these days I am unable to solve B and C quickly , while so many participants are solving B, C and D. :(
unfortunate. needs some action
That's why so many AC's today. Don’t feel upset, they just got some ratings, not skills.
Something has to be done about it.
cheating in problem D is dis heartening , MikeMirzayanov please use moss or some strong plagiarism checker
This issue should be sorted out asap... !!
In the end they could always create a new group. So just participate in contests the right way. You will get better unlike them.
Well codeforces is not giving any type of prizes , there is not any perks for having good rank and definitely, your crush is not going to impress by seeing your rating rather than self satisfication....:) So why mass cheating??
hope so !!!
.
there is one person in our school,he almost can't solve any problem in our school test, but get Master(orange) in codeforces easy.
In China, codeforces Round usually hold in night, in the next daytime, I ask the statement in Chinese of the problem he have passed, he couldn't answer any.
Usually, he even don't know the problem's statement but get the right code.
To protect him, I can't publish his codeforces Id.
sorry for my poor English.
Thanks for releasing the editorial early.
Here are solutions in video format for A-F and my idea for G, although my G probably sucks or something since it failed
I think that there is an easier way to think about H. I don't know why the statement contains an information that for every preference profile there is an unique way to create the permutation, as it says something about the way how to solve the problem, but during the contest I had no idea how to prove it or even why is it true.
We just have to know that after reducing the cycles to single vertices the whole graph has to be acyclic. Calculating the number of labeled DAGs on $$$n$$$ vertices is a well known problem which is solvable in $$$O(n^3)$$$ and we can do a very similar thing here (but the vertices have some kind of weights, so we have to maintain the multiset).
EDIT: by graph I mean the following: if the $$$i$$$-th guy prefers $$$j$$$-th guy instead of the guy that he received the gift from, then let's draw an edge from the $$$i$$$-th to the $$$j$$$-th vertex.
No python solutions passed for E. lol.
PyPy is 32 bit on CF, meaning it will use its big integers for any number that can't fit inside a signed int32. So in order to make PyPy run "fast" on that problem you need to somehow get away from directly working on numbers of size 2^60.
at_f was super close to get AC 102859203 (during the contest) by avoiding big ints, but unfortunately he used a PyPy2 specific trick, and submitted his code in PyPy3. In order to make it work in PyPy3 he just needed to change
int(...)toint(float(...)). He did that after the contest and he got AC 102862814.I did not participate in the round myself, but after the round I did try to solve problem E using PyPy. I've been able to make my solution run in $$$717$$$ ms in PyPy2 102882788. So while the problem is far from unsolvable in PyPy, it is not nice to solve using (32 bit) PyPy.
pog
I have a solution for F that might be more intuitive for people who are familiar with linear algebra.
It's clear that we are asked to find the lexicographically smallest vector basis of the given vectors. The general algorithm for finding the vector basis is to maintain the vector basis of the prefix $$$i$$$. Vector $$$i+1$$$ can be added iif it cannot already be created by some linear combination of the basis of the first $$$i$$$.
Because each vector has at most 2 1's, we only need to check whether we can create a pair or not. First consider the simpler case of $$$k=2$$$. Maintain the same graph as the editorial over each prefix $$$i$$$ vectors. Note that every pair of dimensions as one can be represented by some path between vertices i.e. $$$a$$$ to $$$b$$$. . . to $$$x$$$ represents a vector where only $$$a$$$ and $$$x$$$ are set. We only need to track connected components and and then check if $$$x_1$$$ and $$$x_2$$$ are in the same connected component before adding/ignoring vector $$$i+1$$$.
For the case $$$k=1$$$, note that any vertex in the same component can now become a vector with a single element, i.e. from the path ($$$a$$$ to $$$b$$$. . . to $$$x$$$ then adding $$$x$$$ again to create a vector with only $$$a$$$ set). Any component with one of these vertexes can be merged with any other vertex in any other component with another $$$k=1$$$ vertex. The solution is to maintain one component $$$g$$$ (initially -1) containing all vertexes with $$$k=1$$$.
Can you please explain why we're finding the basis here? The span of the basis will give us $$$T$$$, but how do we know that we only need $$$1$$$s and $$$0$$$s as coefficients while taking linear combinations (to obtain $$$T$$$)?
We're considering the all the operations mod 2 so any coefficient >= 2 will reduce to one < 2.
Thanks.
Nice round to end a terrible year. Happy New Year and high rating to everybody :)
Why greedy solution for C works? Can anyone prove it?
Obviously we will get a palindrome-less string, but how do we now it is optimal?
Without loss of generality suppose palindrome substring is of form $$$aa$$$ then we need to change either first $$$a$$$ or second $$$a$$$.Why changing second $$$a$$$ is optimal ? Because we can also break "future palindromes in that way",for example in $$$aaba$$$ changing to $$$azba$$$ is better than changing to $$$zaba$$$ .
Now suppose substring is of form $$$aba$$$, the we have to change atleast one $$$a$$$ in it for sure . Changing second $$$a$$$ here also is optimal because we will avoid future palindromes (for example if string was $$$abaa$$$ , then changing second $$$a$$$ to $$$z$$$ will make $$$abza$$$ which will break 2 palindromes in single operation unlike changing the first $$$a$$$ to $$$z$$$ which will make $$$zbaa$$$ ).
Also while changing a character we can always make it different from 4 neighboring characters as mentioned in editorial (because there are 26 characters). So in the end there we won't have any palindrome of size 2 or 3 and thus it's impossible to have palindrome of bigger sizes.
Thanks for clarification!
Can anyone explain this dp bitmask solution for C? Submission
Many of the top rated contestant I checked, used this way to solve it.
Alternate approach for problem H :
Consider a digraph with $$$n$$$ vertices, where $$$i\to j$$$ iff $$$j$$$ appears before $$$A_i$$$ in $$$i$$$'s list, or $$$j=A_i$$$, then it's good iff $$$i\to A_i\to A_{A_i}\to \cdots$$$ are the only cycles in the digraph. i.e. consider a cycle in the input as a big vertex, then it's a DAG. This can be solved using a DP which is almost the same as counting DAG. (The state is the number of cycles of each length. For each state, iterator all its subsets as sources and use inclusion-exclusion.)
The complexity will be $$$O(S(n)\cdot n)$$$, where $$$S(n)$$$ is the maximum sum of numbers of subsets of all states, $$$S(40)=29400$$$.
Submission : 102862180
Of course, this can be "optimized" to exactly the same complexity as the intended solution, but due to the extra $$$n$$$ factors, it's not as pratical as the previous one.
Thanks for such an amazing round with such interesting problems (though I screwed C totally :P). But I just had one complaint regarding the stories in the problem statement, It would be great if you could add a divider or something like that which separates the stories, formal definitions, and other redundant stuff from the problem-statement next time :) .
:P
Editorial this fast makes my day :))
Could some kind soul tell me why me solution for E did not pass? I believe my time complexity was O(60n) as well and do not see where my program is inefficient. My code
I tried pre-calculating some stuff but that too did not pass. (code)
here: got rid of TLE
however now it gets MLE on test 6, good luck with that :P
Thanks a bunch! I will try to fix that and will remember these tricks for the future.
I have implemented what you recommended (memoizing the 2^x part and fastio) and surprisingly that was enough for me (code) — a bit depressing that I couldn't find this in contest but thanks for helping and at least I will remember next time!
You've submitted your code in C++14 (which on cf is 32 bit). Your code will run so much faster if you just submit to C++17 (64 bit)!
Pre calculate the powers of 2 modulo M,(wont exceed 60), and try to remove some arrays like andv and orv, they are unnecessary. I think it will be enough.
My O(60*n) java solution passed under the time limits (both during contest and multiple times after contest).
A link here in case u want to see my solution.
In your inner loop you are calling
mod_pow(2,60-j-1)whereThis makes your solution 60 * 60 * n. In general you should never use this kind of mod_pow. Instead use
With this ^ your code will still not be a true 60 * n solution, but at least it will not be as insanely slow. To fix your TLE you should do three additional changes.
Switch to faster IO (Just add
cin.tie(0)->sync_with_stdio(0);first line in main)Submit in g++(64 bit) instead of the 32 bit version you are currently submitting in. 64 bit is pretty much always the better choice, especially for these kind of problems.
Try to not call the mod_pow function in the inner loop at all to get a true 60 * N solution.
When is Hello 2021 going to be?
Thanks for the editorial just check for plagiarism.
Btw F is similar to SEERC 2017 D
My team accepted this task, and by checking the code it looks like, I wrote it, and somehow I completely forgot about it :(
Does system testing use some kind of g++ optimization to make testing faster? I submitted 102853379 during contest which passed pretest 2 but now shows WA. Also it is passing now, but somehow only on my friend's account 102870632 but not mine 102870678
Woah, really unfortunate. The same code passed in 3 out of 6 tries. But it could be UB, if so you can't really blame system for inconsistency.
I guess it's line number
469of your code. It should bedp[0][j]instead ofdp[0][0]Yeah missed that completely, Thank you
In problem D can someone explain that why for k = 2 in this test case the answer is 7999, I believe it should be 7000.
EDIT: Nevermind I got my answer.
Include the {1,2},{2,3},{2,4},{3,5},{3,6},{3,7} in the first color, giving the value 4000, and keep the rest of the edges in the second color giving value 3999. So total would be 7999
My solution for 1466I - The Riddle of the Sphinx only uses $$$3n+2b$$$ queries, I think.
I have a solution that uses $$$2n + 2b - 2$$$; you can read a writeup here.
had the worst contest ever lowest rating of my life
can anyone please tell me why my code is failing at test case 2 https://mirror.codeforces.com/contest/1466/submission/102857149
Happy New Year!
Here's a solution to 1466I - The Riddle of the Sphinx which uses only $$$2N+2B-2$$$ queries, found by scott_wu.
The main idea is that we want to simultaneously bring down $$$B$$$ and $$$N$$$, so we'll maintain a "diagonal" of upper bounds on the input elements in a stack, similar to the editorial solution. We'll actually think of the stack as a sort of cyclic queue, because we'll repeatedly take the item with the highest upper bound and try to reduce it to the next item on the diagonal, so we'll actually phrase this as a deque. More specifically, we will maintain the following:
Then, in each step, we will query $$$lo + 2^b - 1 \overset{?}{<} a_{d[-1]}$$$. Here, $$$d[-1]$$$ refers to the back of $$$d$$$; this is the element with the worst upper bound, and we'll try to reduce it as much as possible.
Intuitively, if we get "no", then we have a tighter upper bound on $$$a_{d[-1]}$$$, so we can cycle it to the front and decrement $$$b$$$. If we get "yes", then our lower bound increases to $$$lo + 2^b$$$, and if $$$lo$$$ increases past some upper bounds, we can eliminate many elements from the front of $$$d$$$ as too small to be the max. In particular, after our first "yes" answer, each following query will actually be querying $$$lo + 2^b = \operatorname{truncate}(lo, 2^{b+1}) + 2^{b+1}$$$, the upper bound of the front of the deque, so a subsequent "yes" will remove at least one item.
More formally,
We will actually continue this algorithm past $$$b < 0$$$ (all our math still works, we can just query $$$\lceil lo + 2^{b} \rceil - 1$$$). We can stop once $$$b + len(d) \le 0$$$, because then $$$lo \le a_{d[\cdot]} < \operatorname{truncate}(lo, 2^{b+len(d)}) + 2^{b+len(d)} \le lo + 1$$$, so we can output $$$lo$$$.
To analyze the runtime, note that each "no" query reduces $$$b + len(d)$$$ by 1, but each "yes" query doesn't change $$$b + len(d)$$$; we need some way to bound the number of "yes" queries. The best monovariant is the number of 0-bits in $$$lo / 2^b$$$, treated as a $$$(B-b)$$$-digit binary number. This increases by exactly $$$1$$$ for each "no" query, and decreases by exactly $$$1$$$ for each "yes" query. Thus, the quantity $$$2(b + len(d)) + \# 0$$$ decreases by exactly $$$1$$$ each query. It starts at $$$2(B-1 + N) + 1$$$, and ends at least $$$2 \cdot 0 + 1$$$ (there is at least $$$1$$$ 0-bit at the last step, since the last query must be a "no"), so we use at most $$$\boxed{2N+2B-2}$$$ queries.
Code: 102868071; this code takes a few implementation shortcuts. Instead of storing $$$lo$$$, we actually store $$$lo + 2^b - \epsilon$$$, i.e. the query string, and update it as we go. Also, $$$b$$$ and the deque are reversed versus this writeup.
On the question of optimality: ksun48 wrote a brute force for $$$N = 2$$$ and the pattern was pretty nontrivial. In general, I think constant-factor optimizing worst case bounds is pretty messy and doesn't typically have a nice closed form, because you have to very carefully split your cases up along nontrivial boundaries. It's very hard to get nice lower bounds beyond the basic entropy arguments.
It's not too hard to prove a lower bound of $$$n + b - 2$$$ (explained below). There's also a simple upper bound of $$$n + 2^b - 2$$$ (keep asking whether some $$$a_i$$$ is greater than $$$lo$$$; if "no" then we can throw away this $$$i$$$, and if "yes" then we can increase $$$lo$$$). So $$$n + b - 2$$$ is essentially sharp for fixed $$$b$$$ (we can't even hope to prove a lower bound of $$$1.001 n - 1000$$$ for all $$$n$$$, $$$b$$$, let alone $$$2n + 2b - 2$$$).
Let's make explicit that this problem is equivalent to a simpler game. The state of this game is a multiset $$$P = [p_1, \ldots, p_n]$$$ of integers. There are two players X and Y. X wins when $$$\max P \le 1$$$, and Y wants to delay this as long as possible. In each turn, X picks some $$$i \in [1\ldots m]$$$ and $$$1 \le r < p_i$$$. Y then either caps $$$p_i \leftarrow r$$$, or subtracts $$$r$$$ from every element of $$$P$$$. Let's write $$$f(P)$$$ for the number of turns X needs to win.
A state in the original problem determines a multiset $$$P$$$ where $$$p_i$$$ is (best known upper bound on $$$a_i$$$) — (global lower bound) + 1. Let's write $$$n \times [p]$$$ for the multiset consisting of $$$n$$$ copies of $$$p$$$, so that the answer to our problem is $$$f(n \times [2^b])$$$.
Actually X can always take $$$i$$$ such that $$$p_i$$$ is maximal (as in your solution). To see this, suppose $$$p_i \ge p_j$$$ and X picks $$$(j, r)$$$. Then $$$(i, r)$$$ would also have been a valid play; we claim it's at least as good as $$$(j, r)$$$. If Y responds by subtracting, then this is clear, since it doesn't matter what index we picked. If Y responds by capping, then this is because $$$r, p_j$$$ are no bigger than $$$r, p_i$$$ (here we use the fact that $$$f(P) \le f(P')$$$ if $$$P \le P'$$$ pointwise in some order).
So the problem of finding an optimal strategy reduces to finding the best $$$r$$$ for a given multiset $$$P$$$; this is where I am stuck. Taking $$$r$$$ big is problematic if B caps, and taking $$$r$$$ small is problematic if B subtracts. We probably want to take $$$r \approx \min P / 2$$$, except when $$$\min P$$$ is considerably smaller than the rest of $$$P$$$ in which case we should take $$$r$$$ a bit bigger. The solution you describe takes $$$r = 2^b$$$, but of course in general there is no reason to expect the optimal $$$r$$$ to be a power of two. If $$$P = n \times [p]$$$ then it seems to make sense to take $$$r$$$ a bit smaller than $$$p/2$$$.
I ran calculations for small $$$n$$$ (where we can compute optimal strategies using some binary search and memoization). Here it seems like $$$f(n \times [p]) \approx c(n, p) \log_2 p$$$ where $$$c(n, p) \in (1, 2)$$$ decreases with $$$p$$$ and increases with $$$n$$$. (E.g. X needs 20 turns starting from $$$[61364, 61364]$$$, but only 19 starting from $$$[61363, 61363]$$$, and $$$19 \approx 1.22 \log_2 61363$$$.) My guess is that $$$\limsup_p c(n, p) < 2$$$ for any fixed $$$n$$$. In general I haven't found any counterexample to $$$f(n \times [p]) \stackrel{?}\le n + 1.5 \log_2 p$$$, but this is maybe a bit optimistic.
As promised, let's prove $$$f(n \times [2^b]) \ge n + b - 2$$$ for $$$n, b \ge 1$$$. If $$$b = 1$$$, then this is clear, since X must take $$$r = 1$$$, and Y responds by capping just one $$$p_i$$$. If $$$b > 3$$$, then either $$$r \le 2^{b-1}$$$ or $$$r \ge 2^{b-1}$$$. In the first case, Y responds by subtracting, and the state of the game is no better than $$$n \times [2^{b-1}]$$$. In the second case, Y responds by capping, and again the state of the game is no better than $$$n \times [2^{b-1}]$$$.
Nice solution
.
My O(60∗N * log(N)) Java solution for E got TLE 3 Sec was a tight limit
Can anyone help me with the challenge problem of A which is mentioned above where n,x<=10e5? Any hints?
In problem E, Apollo vs Pan, Editorial distributed the sum formula from one combined version to bracketed version. Whats that particular topic in maths? I want to know the proof of that. Can anyone redirect me?
It's a nice contest. Participated in a contest after so many months. Iam glad I solved upto D but I was too slow. By the way did anyone have an update about hello 2021 contest.
what should i change in my solution C to get ac 102883253 , thank you and HAPPY NEW YEAR
The issue with your solution is with something this string: abab
There is about 0.1 probability that after 1st 2 operations it will become something like abYY which is high enough to have WA.
I don't think you should use O(..) to analyze a exact value in problem I.
You’re right, I’ll fix.
Happy New Year In advance. At midnight of 31st December 2020 was asking me, So, tell me where shall I go? To the left ...? Where's nothing right Or to the right ...? Where nothing is left.
Why did this bit of code give me TLE? isn't
if-elseO(1)I was able to fix it but I wouldn't have guessed this was the issue
You got TLE not because this bit of code but because of vectorused(200005)
It costs 200005 unit of operations in each of the T tests
.
Great contest and nice editorial!!!!!
Hello everyone! I think I have a counterexample for problem 1466B - Last minute enhancements. I too came across with this approach "we conclude that the result is the number of different elements in the input increased by the number of intervals containing at least one duplicate.", but the reason why I didn't implement it is because I came up with the following example "44566": The previous approach yields 5, since in the beginning there are 3 different numbers (4,5,6), and there are 2 duplicate intervals. However, the real maximum possible number of different notes is 4 (an example being "45676").
Also, I don't think I quite understood the approach of 1466D - 13th Labour of Heracles. Is it only choosing and edge per new colour?
$$$[4, 4, 5, 6, 6]$$$ forms one interval "maximal contiguous intervals of values".
oh, that makes sense. thanks!
For problem C, how does one show that the greedy strategy is optimal (i.e. it requires minimum number of character changes)? The proof stated seems incomplete — it only shows that we can always change the positions to some character which is not the same as the four neighbours!
how did you got LGM with rating of expert ...CF should look into this its like decepting people
You can change your color and username at the end of each year.
I faced an issue when I submitted the solution of B. Same test case gave different answer on my terminal and on codeforces online judge. Here is my code: 102850117
output on my terminal: 5 2 6 1 3// matches the correct outputoutput on online judge: 5 1 6 1 3// 2 expected after 5Could anyone guide me what is causing this abnormal behaviour ?
vector<int> v(n);You're not initializingv. Just change it tovector<int> v(n, 0);and you'll be fine.thanks for replying.
2-month later me wants to correct myself. That's not the problem. Your algorithm is incorrect.
now 4th question was not clear ..like you should have clearly mentioned that k coloring means that we can use k colors to color the graph in anyway we want ..from examples I guessed that we r using 1 color to paint all edges and then every time we we use (n+1)th color then we use that color to paint any "1" edge in graph ...and now if that coloring(edge) is diving graph into 2 components then we have to consider max of 2 ....and in that case this proof will also not hold ...I could be under 3000 rank if you would have mentioned that
Absolutely not. The question was clear.
"from examples I guessed that we r using 1 color to paint all edges and then every time we we use (n+1)th color then we use that color to paint any "1" edge in graph" I don't understand what were you trying to say here at all but maybe next time try looking at the statement instead of guessing from examples.
Will Editorial be translated into Russian?
Any hint for the challenge of problem C?
Think of dp solution and segment tree.
I posted my post-contest stream (explaining A-G) on YouTube: https://youtu.be/KOvQUwtqDis
Editorial's solution to problem D gives WA. It prints too many times the sum.
I also understood why the given solution works and it might be a sort of proof.
The sum of degrees in the tree = 2n-2 (every edge adds 2). For each vertex v starting from the maximum weights, we add its weight deg(v)-1 times. It means that in total we change 2n-2-n = n-2 edges. And this is precisely the number of new colors we have to add (2,..,n-1). This means that every added color gets the maximum possible weight.
Fixed. By an accident, I pasted a solution for the initial version of the problem.
Alternative Solution for G. Song of the Sirens
We can solve it in $$$O(\sum log_2({\sum}))$$$ along with other linear terms. We can see that $$$t_i$$$ is periodic with $$$2^{(ind-i-1)}$$$ where ind is the index of the song. With this observation, in some query string, we must have alternate $$$t_0$$$. Now, if we remove all alternates, we must have alternate $$$t_1$$$ and this goes on recursively till depth $$$log(\sum)$$$. Now, finally, we would be left with a single character always and we can find the number of occurrences by simply storing prefix sums. For help, This is my submission. The code is a bit messy, but it should help you.
Thinking more about it, the concept can be generalized to be solved in linear time with some tricky optimization. The thing to note is this solution does not require KMP or any other such algorithm. Optimized code
$$$S \cdot |s_0|$$$ doesn't look like a linear term.
You can optimize it using hashes. I was a bit too lazy to implement it.
I am trying to understand the solution for D, have gone through the editorial multiple times but still not able to. Can someone please explain their thought process as to how they arrived at the provided algorithm / solution ? Thanks !
At first I understood that in optimal solution subgraphs of all colours must have only one connected component, because if we have two or more we use only one with the biggest weight and all other we can use in another colours. Then I decided to construct solution from 1 colour to n — 1 colour. When we add next colours we just pick a vertex and recolour all edges by the way of one of her edges. By this operation we only add to our sum weight written on picked vertex.(Because all that another vertices are still in one colour, but we incremented number of colours for our picked vertex.) And then it is obvious that if we want max result on every step we must pick the vertex with max weight. Notice that vertex can have one(in this case it cannot be picked) or more than two adjacent edges(in this case we can pick this vertex more than once).
For C, why can you only look at the length 3 ones?
If palindromes length is $$$2n + 1$$$, for some $$$n > 0$$$, then the middle three characters form a palindrome. For example, ab**cac**ba.
If palindrome length is $$$2n$$$, then the middle two characters form a palindrome. For example, bcc**bb**ccb.
Thus, if we remove all palindromes of length $$$2$$$ and $$$3$$$, we won't have any palindromes of greater length.
THX!!!
Could anyone explain me the DP approach for problem C, I have solved it using greedy by myself but didn't grasp the ideal of DP solution. Thanks
For problem E , i have used the same method which is given in this Editorial but still i am getting TLE in 2nd TC..
Here is my Python 3 solution. Can anyone please help!
If we calculate the number of operations, it's $$$n$$$ (outer loop) * $$$60$$$ (inner loop) * $$$\log(10^9+7) \approx 30$$$ (the
pow()'s), which is about $$$1800 \cdot 5 \cdot 10^5 \approx 0.9 \cdot 10^9$$$, which is too much for python to handle. Even some Java solutions were TLE'ing, and C++ solutions without fast input/output[deleted]
Can someone explain how to solve challenge of problem B?
Sort numbers by $$$x_i + k_i$$$, then when analyzing the sequence, change $$$x_i$$$ to the smallest value $$$y_i$$$, such that $$$y_i$$$ hasn't occurred yet, and $$$x_i \leq y_i \leq x_i + k_i$$$. This can be done in $$$\mathcal{O}(n \log n)$$$ with
lower_boundon set.Why sort by xi+ki?
$$$x_i + k_i$$$ is an upper bound of what we can achieve. As we keep replacing $$$x_i$$$ with the smallest possible option, it is intuitive to analyze the elements in this order (because while replacing in some sense, we are not taking what the next elements could take).
Thanks
Can someone explain how to solve challenge of problem A?
The solution 2 of the problem b is wrong.
The explanation says:
"where we analyze the elements in nondecreasing order"
But then the code doesn't actually sort the elements in nondecreasing order. Sample test case that gives wrong result:
1 3 5 6 5
Solution one gives correct result (3) solution two gives wrong result (2)
Does getting row reduced echelon form of the matrix for F work?
Sorry for necroposting, but I am not able to understand the editorial for problem D, specifically what is the proof trying to prove? How does finding $$$\sum^{n}_{v=1}c_i = n + k - 1$$$ for $$$k$$$ coloring proves the fact that we have to choose the vertex with maximum weight for $$$deg(v_i)-1$$$ times?