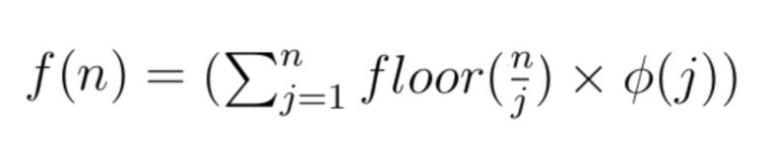
Here floor is floor function or greatest integer function and phi is Euler totient function.
For n < 10^4 i tried to find the f(n), and turn out to a simple expression :
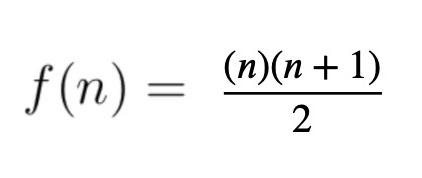
Can you provide a proof or some argument related to this expression
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3985 |
| 2 | jiangly | 3814 |
| 3 | jqdai0815 | 3682 |
| 4 | Benq | 3529 |
| 5 | orzdevinwang | 3526 |
| 6 | ksun48 | 3517 |
| 7 | Radewoosh | 3410 |
| 8 | hos.lyric | 3399 |
| 9 | ecnerwala | 3392 |
| 9 | Um_nik | 3392 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 169 |
| 2 | maomao90 | 162 |
| 2 | Um_nik | 162 |
| 4 | atcoder_official | 161 |
| 5 | djm03178 | 158 |
| 6 | -is-this-fft- | 157 |
| 7 | adamant | 155 |
| 8 | awoo | 154 |
| 8 | Dominater069 | 154 |
| 10 | luogu_official | 150 |
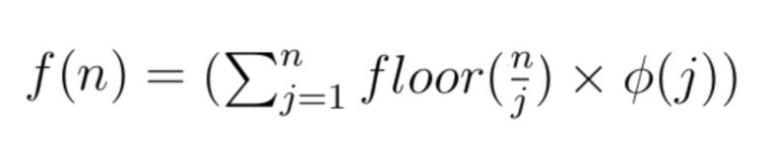
Here floor is floor function or greatest integer function and phi is Euler totient function.
For n < 10^4 i tried to find the f(n), and turn out to a simple expression :
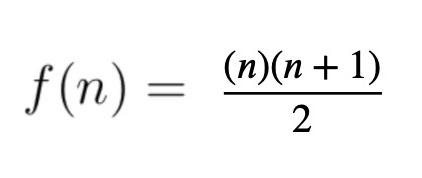
Can you provide a proof or some argument related to this expression
| Name |
|---|



Auto comment: topic has been updated by sobhagyaSD (previous revision, new revision, compare).
It's correct, here's my proof.
Got it, Thank you so much.
And the "famous lemma" indeed can be proven easily with induction over.