yermak0v's blog

Array sorting with O(n) complexity
By yermak0v, 11 years ago, translation, In English

Hi all.
Once upon a time I'm wrote about trie and profit and how useful it can be if use it for other purposes. link
In a word, if write a counting sorting, and use trie as associative array instead of the usual array, then can be achived O(n) complexity with not big constant. That is just add all numbers to trie and after it view all states with dfs (by that review all states in lexicographical order).
But would have to sacriface memory, because anyone vertices contains links to next stats.
P.S. To work correctly, all numbers must be completing with leading zeros.
UPD. code
I wonder will it be profitable to use this sorting instead of quick sort or another sort with O(n * log(n)) complexity.
P.P.S. Sorry my poor English.

  • Vote: I like it
  • +4
  • Vote: I do not like it

»
11 years ago, # |
  Vote: I like it +3 Vote: I do not like it

Well, if we have an array of integers, then fast implementations of quicksort are the right way to go. While regular quicksort has worst case performance of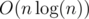 , its constant is so low that it's hard to beat it in real-time performance.

The trie approach bases on constant number of bits. However, when the sorted numbers are in the range [0, n) (still, that's a very special case), then it's enough to use CountSort; otherwise, we need to remember the numbers as strings of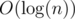 digits, so building the trie takes 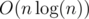time anyway.

→ Reply