Overview
In DIV 1, there are 4 interesting problems together with a normal one. We think it is reasonable because we can't have a round fullly with intelligence. Problem A, C have weak pretests while others intended to be strong. About more then 200 participants solve A in the early 45mins, then a few of them start from C while most of the other start from B.
Problem B is a rather standard problem, but if you're unfamiliar with the algorithm, it can be very hard. Problem C is a more intersting problem. As the name implies, there was a similar version in the previous round before, but this time it has a brand new constrains.(So here we have a psychology experiment: could different constrains make people thinking in a slightly different way?ww)
The standard solution of problem C is O((b - a) + nlogn). The first expected correct solution was written by zeliboba. http://mirror.codeforces.com/contest/346/submission/4512654
After that, some people start to solve problem D. Problem D looks like a hard dp problem on a graph at the first glance, the key point is how to avoid the circle in the transfer equation. It turn out to be elegant after you could found a right order of the evaluation. Problem E is challenging which you need find a way to transform the original question into a smaller scale, and cut off many many corner cases ... And in the very end, you find a way like binary search to get O(logn) as the time complexity. No one manage to solve problem E during the contest, maybe Petr is the man who closest to it.
The winner comes to cgy4ever, because he found the draw-black in his previous C submission during the very beginning even when there is nobody hack him! He resubmit it decisively and get back when finished problem D. After that, he use the same trick which made him failed before to hack others and got a handsomely rewards. The second place went to rng_58, because of the combination of decent speed in A, B, C, D.
Problem B belongs to me, problem C belongs to CMHJT and others belong to UESTC_Nocturne. The illustrator of problem C is Chairman Miao(貓主席).
Editorial
Problem A. Alice and Bob
Brief description:
Alice and Bob play a game, the rules are as follows: First, they will get a set of n distinct numbers. And then they take turns to do the following operations. During each operation, either Alice or Bob can choose two different numbers x and y from the set, as long as |x - y| is not in the set, then they add it to the set. The person who can not choose two numbers successfully will lose the game. The question is who will finally win the game if both of them do operations optimally. Remember that Alice always goes first.
Analysis:
First, no matter what happend, the number set we get at the very endding will be same all the time. Let's say d = gcd{xi}. Then the set in the endding will be some things like {d, 2d, 3d, ... max{xi}}. So there is always max{xi} / d — n rounds. And what we should do rest is to check the parity of this value.
Problem B. Lucky Common Subsequence
Brief description:
You have been given two strings s1, s2 and virus, and you have to find the longest common subsequence of s1 and s2 without virus as a substring.
Analysis:
This is a rather classical problem, let's say if there is no virus, then it is the classical **LCS ** problem. You can solve this by a O(n2) dynamic programing.
When consider about the virus, we should add 1 more dimension on the state to trace the growth of the virus. It can be done by wheather Aho-Corasick automation, or KMP when there is only one virus in this case. The overall time complexity is O(n3).
Problem C. Number Transformation II
Brief description:
You have a number b, and want to minus it to a, what you can do in each step is weather subtract 1 or b mod xi from b. And we ask what is the minimum number of steps you need.
Analysis:
I bet there is a few people know the greedy method even if he/she have solved the early version before.
Codeforces #153 Div 1. Problem C. Number Transformation
Let dp[k] denotes the minimum number of steps to transform b+k to b. In each step, you could only choose i which makes b+k-(b+k) mod x[i] minimal to calc dp[k]. It works bacause dp[0..k-1] is a monotone increasing function. Proof: - Say dp[k]=dp[k-t]+1.If t==1, then dp[0..k] is monotone increasing obviously.Otherwise dp[k-1]<=dp[k-t]+1=dp[k] (there must exist a x[i] makes b+k-1 also transform to b+k-t,and it is not necessarily the optimal decision of dp[k-1]). So dp[k] is a monotone increasing function, we can greedily calc dp[a-b].
In the first glance, it looks like something which will run in square complexity. But actually is linear. That is because, we could cut exactly max{xi} in each 2 step. It can be proof by induction.
So the remians work is to delete those same xi, and watch out some situation could cause degeneration. Many of us failed in this last step and got TLE
Problem D. Robot Control
Let's dp from t to s.
dp[u] = min(min(dp[v]) + 1 , max(dp[v])) | u->v
Here dp[u] means, the minimum number of orders mzry1992 needs to send in the worst case. The left-hand-side is sending order while the right-hand side is not. At the beginning, we have dp[t] = 1, and dp[s] will be the answer.
We can see there is circular dependence in this equation, in this situation, one standard method is using Bellman-Ford algorithm to evaluate the dp function.
But it is not appropriate for this problem.
(In fact, we add a part of targeted datas in pretest, these datas are enough to block most of our Bellman-Ford algorithm, although there is still a few participator can get accepted by Bellman-Ford algorithm during the contest.
Check rares.buhai's solution
dp[u] = min(min(dp[v]) + 1 , max(dp[v])) | u->v
The expected solution is evaluating the dp function as the increased value of dp[u] itself. Further analysis shows, wheather we decided sending order or not in u can be judged as the out-degree of u.
while (!Q.empty()) {
u = Q.front(), Q.pop_front()
for each edge from v to u
--out_degree[v]
if (out_degree[v] == 0) {
relax dp[v] by dp[u]
if success, add v to the front of Q
}
else{
relax dp[v] by dp[u] + 1
if success, add v to the back of Q
}
}
Check Ra16bit's solution to see how it works.
Problem E. Doodle Jump
Brief description:
You have been give a, p, n, h (gcd(a, p) = 1), For each ai mod p, (i∈[1, n]), check weather the maximum distance in neighborhood after sorting is <= h.
Analysis:
Take a =5, p =23 for example ... Divided the numbers in group.
0 5 10 15 20
2 7 12 17 22
4 9 14 19
1 6 11 16 21
3 8 13 18
We start a new group when the number > P
We found the difference between the elements of the first group is 5, The subsequent is filling some gap between the them ...
After some observation we could found that we should only consider into one gap ...(e.g. [0, 5] or [15, 20] or [20, 25] ... )
0 5 10 15 20
2 7 12 17 22
4 9 14 19
1 6 11 16
That says .. a =5, p =23 is roughly equal to some things in small scale?
So let's check it in detail. Lemma 1. In any case, the gap after 20 won't better than any gap before it.
0 5 10 15 20
2 7 12 17 22
4 9 14 19
1 6 11 16
For example, in this case, the gap after 20 is: 20, 22 And it has 16 in [15, 17] but no 21.
Is there any chance that [20, 23] is better than [15, 20]?
No, that is because, when there is no 21, then (19+5)%23 = 1, go to next floor. and there is no corresponding gap after 20 ([22, 24]) for this gap ([17, 19])
So we only need to consider [15, 20] ... and we found [15, 20] is roughly equal to [0, 5]
e.g. : 15 20 17 19 16 18
equal: 0 5 2 4 1 3
we say 'roughly' because we havn't check some boundary case like there is 3 but on 18 ...
0 5 10 15 20
2 7 12 17 22
4 9 14 19
1 6 11 16 21
3 8 13
If it happend, we should remove the number 3. .. If we can remove the element 5, then we can from a=5, p=23 to a'=2, p'=5 ...(n' = an/p, a' = a-p%a, if there is 3 but no 18, n'=n'-1)
The rest things is to discuss wheather 5 is necessary or not.
Let's we have:
0 2 4
1 3
If the 2*n'<5, then there is only one floor, the answer is max(2, 5-2*n'). If there is more than one floor, we could conclude that 5 is useless.
Proof: Elemets in 1st floor is:
0 a 2a 3a ...
Let's say the maximum elements in 1st floor is x, then the minimum element in the 2nd floor is b0 = x+a-p, because b0 — a = x-p, so the difference between b0 and a is equal to the difference between x and p. That is, we can consider [b0, a] rather than [x, p], when there is a element insert in [b0, a], there must be some element insert in [x, p] in the same position.
So we have have succeeded to transform our original problem into a small one. Of couse, this problem havn't been solved, we haven't consider the time complexity. Says a' = a — p%a, when p = a+1, then a' = a-1, but we have a equal to 10^9, it won't work.
But, let's we have A1, A2, ... An ... and we subtract d from all of them, the answer won't be changed. So we can use p%a substitute for a-p%a, this is equivalent to we subtract %p% from all of them ...
So we set a' = min(a-p%a, p%a), so a'<=a/2, therefore, the final time complexity is O(logn).
You can check Petr 's solution for detail.










there is a typo: "... the classical LCA problem ..." => LCS
Thank you. Fixed. m(_ _)m
Actually our standard solution to C is O(b-a+n). O(b-a+n),O(b-a+nlogn),O((b-a+n)logn) are all able to pass during the test.
oh, never mind
For Problem B: Can you Explain little bit more on How "Aho-Corasick automation, or KMP" can help in figuring out smallest string that does not contain virus.
For B, I already had the intuitive idea that this problem will be solved by either Aho-Corasick algorithm or KMP with dp, but I could not formalize the idea of states transition in dp. Could you please just provide the state in your dp algorithm??
Original problem can be solved by dp with two parameters DP[Len(s)] [Len(t)]. http://en.wikipedia.org/wiki/Longest_common_subsequence_problem
To solve B you need to modificate it to DP[Len(s)][Len(t)][Len(virus)-1] where third parameter means maximum length of suffix of LCS that equal to prefix of virus.
To easy check where we go from K state (third parameter) by character C we can make automat on prefix function by virus.
Then if we stand in DP[i][j][k] :
1) if(s[i] == t[j] and Automat[k][c]<Len(virus) we try to relax DP[i+1][j+1][Automat[k][c]]
2) Try to relax DP[i][j+1][k] and DP[i+1][j][k]
UPD My solution: http://mirror.codeforces.com/contest/346/submission/4532899 (hope it understandable)
got it, many thanks to you man :) Also understood why KMP tag mentioned in the problem.
1) Can you please explain what "maximum length of suffix of LCS that equal to prefix of virus" means? 2) What is an automat?
1) We stand in DP[i][j][k]-state (in which we store longest LCS), virus = "virus"
Let's go from k = 0 to 4,then:
KMP
2) http://en.wikipedia.org/wiki/Automata_theory
Can't find nothing about automaton on prefix-function in english. I hope you will be able understand this with some translator (google translate for example).
Fortunately, the e-maxx article on Prefix function has been translated in English and can be found here: prefix-function: automaton on prefix-function
My solution for B got a WA on test 41 and I don't know why :<, please help me with this code: https://mirror.codeforces.com/contest/346/submission/109283664.
"So the remians work is to delete those same xi, and watch out some situation could cause degeneration. Many of us failed in this last step and got TLE", I really could not understand this. What you you mean by degeneration in this case? Please explain this last important step.
suppose b=1, all x[i]>a, what will happen?
As b = 1, All x[i] > a. Then a % x[i] = a. So if we take this, then we will lead to a — a = 0, which is less than b. So we need to move one by one, so answer would be a.
In Alice and Bob problem how do you prove that you will always get {d, 2d, 3d, ... max{xi}} in the end. It is easy to see but I am unable to prove it.
I convinced myself like this:
In details:
See Euclidean algorithm for finding GCD. If you will look into the description or code you will see that it does exactly what is asked in this problem — subtracts numbers one from another. And the result is GCD of original two numbers. So you can see that by some sequence of subtractions you can get GCD.
If you already have d which GCD of all the numbers then you can easily fill all the gaps in { d, 2d, 3d, ..., max } sequence by starting subtracting d from { max, max — d, max — 2d, ... }. So you will get the intended set.
You cannot subtract two numbers a and b which have GCD(a, b) = d and get result which won't be dividable by d. So if you start with set where every numbers can be divided by d then no matter what you subtract you will always have the result which is also dividable by d.
Yes, got it. Thanks!!
Thanks
Is this the final editorial (except the D problem) ? The explanations to problems B and C are very limited and not at all well elaborated.
can you tell me that why the number of rounds in Problem A will be max(xi)/d-n ? How do you come to this point ? can you please tell me this as am not to figure out this thing ? thanks in advance.
take example
3 9 54
gcd (3, 9, 54) = 3
Now total rounds possible including (3, 9, 54) =
all multiples of 3 upto 54
3, 6, 9, 12, 15, 18 ... 54
So total count of these numbers = 54 / 3 = 18.
Now as out of these numbers 3 numbers are already taken, so subtract 3
so rounds remaining = 18 — 3 = 15
Now it is very easy to generalize for 3 being d and 54 being n
answer would be n / d — n.
I hope it is clear now :)
yes, it is more clear to me now. but one thing is that how did you approach to gcd thing ? I understood the problem, the logic and all. how did you approach that it will be done using gcd thing and all ? thanks in advance.
My Ideas during solving the problem:
all the examples had gcd 1. So I directly thought answer as max(xi) — n.
But I thought it can not be too simple, I need to think more.
So I took a case 2 4 6, I immediately found I am wrong in this case.
Then the idea came into mind that if gcd of numbers is g. then we can not create any number not divisible by g because (g *k1 — k * k2) = g * (k1 — k2).
So Finally I coded it and got accpeted :)
given the numbers a1, a2, ..., an, what is the minimum positive value you can achieve by combining them?
Let's write down the equation: a1·x1 + a2·x2 + ... + an·xn = d, where x1, ..., xn are some unknown integers.
It is, as you can see, none other than linear Diophantine equation. And it is known there is no solutions if d is not a multiple of gcd(a1, a2, ..., an)
@hellodear-the final set will contain all elements {d,2d,3d,..max(Xi)} (d=gcd of all elements) so total no. of elements in final set =max(Xi)/d since initially we have 'n' elements total no. of new elements to be added in set to make it complete=(max(Xi)/d)-n.. hope this helps you..:)
in this thing, I was applying some game theory, but it doesn't include anything like that. when the question says optimally, then how do you form examples so as to test your code on them ? because optimally means in the best they can. can you elaborate ? thanks to you.
optimality argument is simple and also given in the editorial itself.
As total you numbers finally would be {d, 2 * d,, .,, max (xi)}.
Hence whatever you add to the these set, no other person will be able to add that as he has to add a new number everytime to this test.
So outcome depend on the parity of turns.
I think the complete proof for A.Div1 is not that much straightforward. Maybe I'm making it too much difficult, but this is my complete proof:
First by induction, we prove that the numbers in the end will be a, 2a, ... , max(ai). Let g = gcd(a1, a2, ... , an). It's trivial that in the end min(ai) ≥ g. Assume that min(ai) ≥ g, because our numbers will be min(ai), 2min(ai), ... , max(ai), so we would have a new gcd. That's a contradiction, so min(ai) = g and our numbers will be g, 2g, ... , max(ai). Each move adds one number and in the end there will be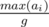 numbers, so the answer wil be the parity of
numbers, so the answer wil be the parity of 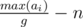 .
.
Sorry for my bad English.
What about this test
2 3 5? min(ai) ≠ gcdOops. You've meant that a — is the result. Sorry.
But how to prove that there is always a way to choose x and y while the number of the current round less than the maximum number of rounds? (Div2C)
If gcd{xi}=1, then for every xi there must exist ti to make sum{xi*ti}=1.
(For example, x1=5,x2=7,then t1=3,t2=-2.x1*t1+x2*t2=1.)
And sum{xi*ti} can be performed in a few turns. ( (5-(7-5))-(7-5). )
And if we can get 1, then what number between [1,max{xi}] can't we get?
if gcd{xi}≠1.the proof is similar.
Why there is must exist such t[i]?
You must know if gcd(a,b)=1, there must exist x and y to make ax+by=1. It can be proved from this.
So.. If we divide all the numbers by GCD, and after that a pair of coprime numbers have appeared, we always can reach 1. Let's choose coprime x and y, then |x - y| will be also coprime with x and y, and it will be less then max(x, y). So we can choose mid(x, |x - y|, y) = x1 and min(x, |x - y|, y) = y1, and they are coprime, and |x1 - y1| will be less than x1. And etc. by induction. But what to do if there is not a pair of coprime numbers after dividing by GCD? For example
35 45 63.63*2+45*5+35*(-10)=1
Because gcd (35,45)=5, we can consider 35 and 45 as one number 5x. Because gcd(5,63)=1, so there must exist x,y to make 5x+63y=1.
So here comes a tragedy. We can get 5 first. Then we use this number together with 63 to make 1.
Someone please explain the greedy idea of (Div 1 C) (Number Transformation II). Thanks in advance :)
It's a pretty simple greedy idea: Just pick the
xthat makes the value ofasmallest after applying the operationa = a - a%x(or subtract 1 if no choice forxmakesasmaller). The proof why this works is given in the editorial: it is never better to get a larger number, so you should get the smallest one you can.As listed on the last paragraph of the editorial you have to be careful to remove all
xthat are either duplicates or cannot be used anymore (a - (a%x)is smaller thanb), otherwise you will get TLE.how to find this x for each number?
we will iterate on all x[i]s and only delete x[i]s when x[i] > a?
Iterate through all x[i]s and delete them when a — (a%x[i]) is smaller than b (if you only delete when x[i] > a, you will also get TLE).
I'm really striving to understand why the algorithm turns out to be linear instead of quadratic... I know the editorial says "That is because, we could cut exactly max{xi} in each 2 step.", but I can't really get what it means :\
Can you give me a hint? Thanks :)
I have an easy intuition of cutting at least max{xi} in O(1) steps, not sure what was the intended 2 step proofs though. I am going to use xi to refer to max{xi}, and assume that proper care is taken to only keep the relevant xi's.
When we do a-(a % xi), we bring caused a to be the next largest integer <= a that is a multiple of xi, since now new_a % xi = 0. Then, if a is divisible by xi, you can do.., do a-1 (causing it to be non-divisible by xi), then finally a-(a%xi) again. In this 3 step sequence you have brought a down to the next lower multiple of xi, and have essentially cut max{xi} in O(1) number of steps.
Sample code : http://mirror.codeforces.com/contest/346/submission/4545367 Yeah I used tree set so it's not exactly O(n).. but hash set keeps giving me TLE :(
Thank you very much, that was really eye-opening! This is why I love Codeforces, great community! :)
Please explain why the problem is solved through the GDC (A)? I tried like this, but I still can not understand why you can not do. Please give a short test on which the decision falls.
Because only those numbers are possible in the game which are multiple of gcd. See this simplest test case
The only number possible in the game is (6-4) i.e. 2, but in your code u are assuming that somehow these (1,2,3,5) numbers can be obtained which is a wrong assumption.
Explain please, how to do Div1-D
i didn't understand Div 2 — D can someone explain it to me please
problem B,ac automachine is doing the thing that belong to kmp
For Div1_E: Should the "Doodler" jump over the platform which H = P ? I just confused about that.
OK I got the answer.
still waiting for D tutorial ...
.. Update .
In my approach to problem div1 B, I calculated longest common subsequence, prepended virus to it, calculated the Z function and deleted every character which had z[i] >= virus.size(). I don't think my approach is wrong. Can someone tell me if my code is wrong or the approach has some flaw. Thanks. Submission : http://mirror.codeforces.com/contest/346/submission/11491420
Can someone explain how to solve this problem 346B - Lucky Common Subsequence? I have went thorugh the editorial but I could not understand.