Hello Codeforces!
Today was Codeforces Round #720 (Div.2), in which I solved problem D — Nastia Plays with a Tree. As I find my solution different from the solutions I heard of after the contest, I will explain it in detail in this blog post. I will note that you still might find value in reading this if you solved the problem, as my proposed solution also maintains at every stage the graph being a forest (i.e I don't create any cycles).
The Solution
Note that in this editorial, when I write simple path, I mean a simple path between two nodes without having extra edges going from any of the nodes that do not belong to that simple path, or simply a node not connected to anything (this will be clearer once we see drawings).
We should first note that bamboo is simply a tree that looks like a single line of connections (i.e a simple path).
We observe that given the sequence of moves the order we delete/link edges in does not change the resultant underlying graph. We consider the following question: how can we delete edges such that we can link the remaining forest via link operations to make a bamboo after we delete all of them?
Well, we want to achieve a simple path in the end, and a simple path can only be broken into nonintersecting simple paths, therefore after edge deletions, we should have a set of nonintersecting simple paths.
Now, our motivation is to take some pen & paper and draw how such a set looks like (not necessarily the optimal one) (in this editorial I cheat with CSAcademy Graph Editor). **Note that for convenience and as in many tree problems, we root the tree at an arbitrary node.
Suppose we are given the following tree (rooted at node 1): 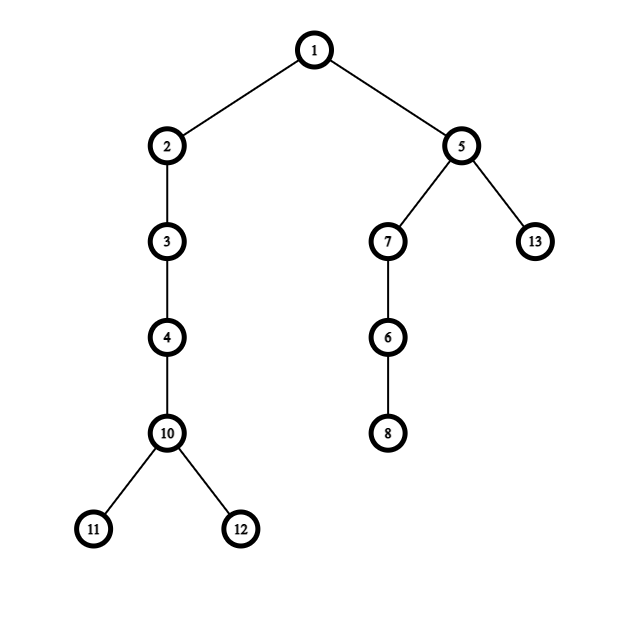
We can convert it to a set of non-intersecting simple paths in multiple ways, one of which is deleting 4->10, 5->13 & 5->7, and if we were to apply this way we would end up with the following set of simple paths: 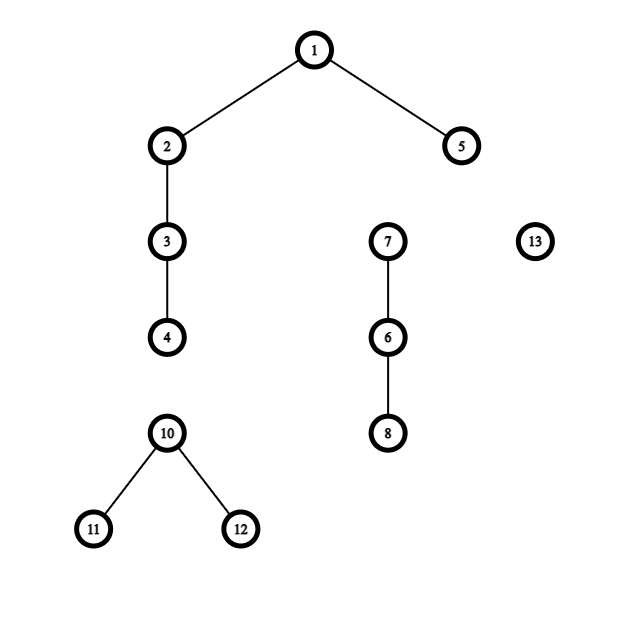
If we look at subtrees of the original tree and what they turned into after the deletion, we observe that if a node has outgoing edges to 2 of its original children from the original subtree then that node must not be connected to its parent.
This leads to an approach of dynamic programming over subtrees & an observation is that we can utilize the following state: whether or not our subtree root is connected to its parent. The motivation for this state is exactly what we state above, in order to connect to more than 1 child we must not be connected to our parent.
Let $$$sdp[c]$$$ be the minimum cost to convert $$$c$$$'s subtree into a set of disjoint simple paths, given that we delete the edge from $$$c$$$ to its parent, and let $$$cdp[c]$$$ denote the cost given that we do not delete the edge from node $$$c$$$ to its parent. So in $$$sdp$$$ we allow connecting to 2 children and in $$$cdp$$$ we do not allow that, but for $$$sdp$$$ we add a cost of 1 (deleting the edge to the parent). Note that in this way, the root $$$sdp$$$ 's value will contain 1 more than the actual answer (because the root doesn't have a parent so we add 1 for no reason) but as you'll see we don't use that numerical value in our construction.
For the construction, when we calculate the $$$dp$$$ values we also the children that we keep edges to. let $$$cn$$$ be an array that will store the connections for the $$$cdp$$$. We will assign $$$-1$$$ to $$$cn[c]$$$ if we don't connect anything, and otherwise, we will assign the label of the node that we connect to (note that in this $$$dp$$$ we can connect to almost 1 child because we are already connected to our parent). Furthermore, let $$$sn$$$ be an array of pairs such that it will store the connections for the $$$sdp$$$. We will assign $$$-1$$$ to $$$sn[c].first$$$ if we make no connections. otherwise, we will assign one of the connections to it. Moreover, we will assign $$$-1$$$ to $$$sn[c].second$$$ if we make less than 2 connections, otherwise we will assign to it the label of the node we connect to that we did not assign to $$$sn[c].first$$$.
By using $$$cn$$$ & $$$sn$$$ we will be able to know given the state (connected or not connected to parent) what edges we chose to keep (i.e, the connections we still have).
Now, we shall discuss calculating the $$$dp$$$ values. Obviously, we want to do this via a DFS scan so that when we calculate the $$$dp$$$ value for a node, we have already calculated the $$$dp$$$ value for all children of the node. Note that for leaves $$$cdp[c] = 0$$$ & $$$sdp[c] = 1$$$ *(again, in $$$sdp$$$ we add 1 for the cost of deleting the edge to the parent). We shall now discuss the calculation for nonleaf nodes.
For both $$$dp$$$'s, we are able to choose for some finite number of nodes the $$$cdp$$$ state (namely, leaving them connected) ($$$\le 1$$$ nodes for $$$cdp$$$ & $$$\le 2$$$ nodes for $$$sdp$$$), and the $$$sdp$$$ state for all of the rest of the nodes (the nodes that we did not leave connected). So if we choose for some child $$$e$$$ the $$$cdp$$$ state rather than its $$$sdp$$$ state, it's good to do that if and only if $$$cdp[e] < sdp[e]$$$ & by doing that we reduce our answer by $$$sdp[e] - cdp[e]$$$, as we use the $$$cdp$$$ instead of the $$$sdp$$$, so for all children $$$e$$$ of node $$$c$$$ we calculate this difference, and we store the 2 biggest differences and the nodes that cause them as they will contribute to us the most. we also calculate the sum of all $$$sdp$$$ values of all children, as that's our worst-case value and we will subtract from that the differences that we get by leaving children connected. We will denote this sum by $$$sm$$$. Additionally, we will denote the biggest difference ($$$sdp[e] - cdp[e]$$$) by $$$d_0$$$ & the child that causes this difference by $$$e_0$$$. Furthermore, if $$$c$$$ has more than 1 child we will denote similarly to $$$d_0$$$ & $$$e_0$$$, the second biggest difference that a node causes by $$$d_1$$$ and the node that causes this difference by $$$e_1$$$. Note that we can find all of these values in $$$O(n)$$$ via keeping a heap of 2 min pairs or simply in $$$O(n\log(n))$$$ via sorting. Now we simply have a bunch of casework (as you have already seen, this solution contains a bunch of casework). id $$$d_0 \le 0$$$, switching to $$$cdp$$$ wont make anything better so we use $$$sdp$$$ for all children (i.e delete the connections to all children) $$$sdp[c] = 1 + sm$$$, $$$cdp[c] = sm$$$, $$$cn[c] = -1$$$ & $$$sn[c].first = -1$$$, $$$sn[c].second = -1$$$. Now, if $$$d_0 > 0$$$, then we have 2 cases: if $$$c$$$ has only one child or it has more than 1 child and $$$d_1 \le 0$$$, then only connecting to $$$e_0$$$ will make things better, so $$$sdp[c] = 1 + sm - d_0$$$, $$$cdp[c] = sm - d_0$$$, $$$cn[c] = e_0$$$ & $$$sn[c].first = e_0$$$, $$$sn[c].second = -1$$$. The second option is that node $$$c$$$ has more than 1 child & $$$d_1 > 0$$$. In this case, $$$cdp$$$ & $$$cn$$$ are the exact same as we can only take 1 node & $$$e_0$$$ both improves our answer & is the best node to do so as it's difference $$$d_0$$$ is the biggest difference. However, now we can take 2 nodes for $$$sdp$$$, so $$$sdp[c] = 1 + sm - d_0 - d_1$$$, $$$sn[c].first = e_0$$$ & $$$sn[c].second = e_1$$$.
Now we know in each state what nodes each node connects to, and our task now is to get a list of the chains in the optimal state. let $$$chain[c]$$$ be {-1, -1} if $$$c$$$ is not the LCA of an existing chain, or a pair of both endpoints of that chain otherwise. we can calculate this array via a second DFS scan, keeping the current state of the root (connected to parent / not connected to parent), the chain LCA if we are members of a chain right now and at want position in the pair to put the end of my chain if so. For more details, see my submission from the actual contest — 115613655 (the function $$$dfs2$$$).
now by iterating over all nodes, we collect all chains, and our task now is to simply connect them. Note that because each node is a member of some chain this implies the root is a member of that chain and the root must be the LCA of that chain therefore chain[root] != {-1, -1}. for all other chains, the corresponding removed edge to them is p[LCA], LCA. we will use a $$$tail$$$ variable, each time connecting one of the endpoints of the current chain to this tail then setting the tail to be the endpoint we did not use (this also works if the chain is a single node because it's both the head and the tail). In the beginning, set $$$tail$$$ to be $$$chain[root].second$$$. Iterate over all other chains and for the current chain disconnect $$$p[i]$$$ -> $$$i$$$ & connect $$$tail$$$ -> $$$chain[i].first$$$, then set $$$tail$$$ to be the other endpoint, namely, $$$chain[c].second$$$. this way we chain all of the chains and we solve the problem!
Complexity: $$$O(n)$$$ or $$$O(n\log(n))$$$, depending if you use a heap of 2 elements or sort in order to find $$$d_0$$$, $$$e_0$$$, $$$d_1$$$ & $$$e_1$$$
This was very challenging to implement during the contest yet eventually I got AC 10 minutes before the end of the round. Thanks for the contest! :D











Auto comment: topic has been updated by lior5654 (previous revision, new revision, compare).
Auto comment: topic has been updated by lior5654 (previous revision, new revision, compare).
I will note here that my first idea was to simply guess that we should only keep a diameter and remove all other edges. I heard others in the community tries the same approach & failed. Here is a counterexample to that approach: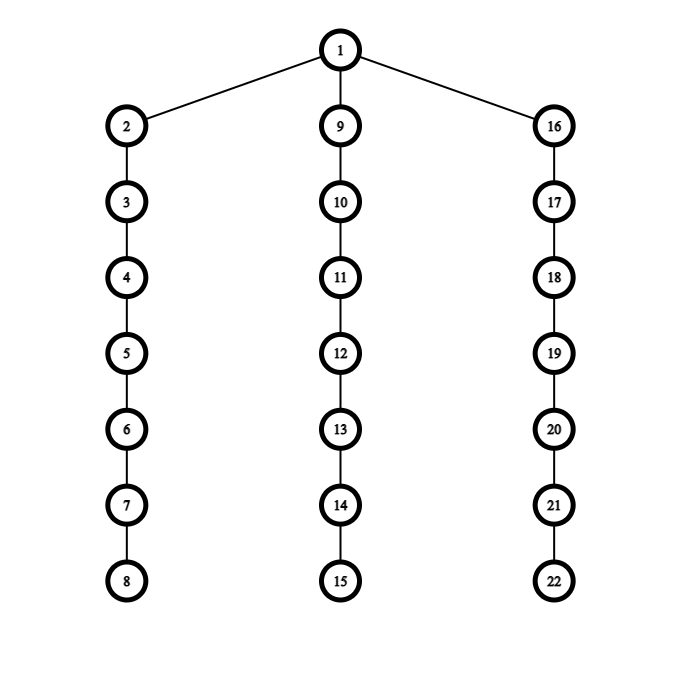
The answer is 1, but the diameter idea will give an answer of 7.
Don't remove all other edges. Recursively go to the child and find it's diameter too and attach one end of child diameter to it's parent's diameter.
A better example of why recursively finding the diameter is not optimal is
Recursively finding the diameter will cut 2 edges, but it is optimal to cut only edge 1-3
Thank you for this editorial!
Also posted here: https://cp-notes.com/notes/fivesixfivefour/CodeForces/1521/D
To learn more about cp-notes, read this blogpost: https://mirror.codeforces.com/blog/entry/90384
Ok i got it from your code. It seems that after calculating the sdp[] , cdp[] and where from a given node we can go next (i.e should we connect it to two, one or no node), the structure of set of simple paths become unique? and by using dfs2() we are just tracing back those paths?
Do we need to cut the 5-13 edge in the example?
Note that the example I gave does not give the optimal solution, it's just an example of a valid way to delete edges such that after that only if link operations we can make a bamboo. And no, we do not.
I see, thanks!
Calculating cdp[] ,sdp[],cn[] and sn[] is fine but after calculating all these stuffs how do we find the chains? It's bit unclear.