1526A - Mean Inequality
Setter: antontrygubO_o
Preparer: errorgorn
Notice that the array size is even length. Usually in such problems, we would split the array into $$$2$$$ equal parts. Can you figure out what those $$$2$$$ parts are?
We sort the array and split it into the big half and the small half.
The main idea is that we can split the numbers into the two halves, the big half and small half, we can place the bigger half at the odd positions and the smaller half at the even positions.
This works because the smallest big number is larger than the biggest small number. Hence, the mean of any two small numbers is smaller than any big number, and the mean of any two big numbers is bigger than any small number.
//雪花飄飄北風嘯嘯
//天地一片蒼茫
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <ext/rope>
using namespace std;
using namespace __gnu_pbds;
using namespace __gnu_cxx;
#define ll long long
#define ii pair<ll,ll>
#define iii pair<ii,ll>
#define fi first
#define se second
#define endl '\n'
#define debug(x) cout << #x << " is " << x << endl
#define pub push_back
#define pob pop_back
#define puf push_front
#define pof pop_front
#define lb lower_bound
#define ub upper_bound
#define rep(x,start,end) for(auto x=(start)-((start)>(end));x!=(end)-((start)>(end));((start)<(end)?x++:x--))
#define all(x) (x).begin(),(x).end()
#define sz(x) (int)(x).size()
#define indexed_set tree<ll,null_type,less<ll>,rb_tree_tag,tree_order_statistics_node_update>
//change less to less_equal for non distinct pbds, but erase will bug
mt19937 rng(chrono::system_clock::now().time_since_epoch().count());
int n;
int arr[55];
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin.exceptions(ios::badbit | ios::failbit);
int TC;
cin>>TC;
while (TC--){
cin>>n;
rep(x,0,2*n) cin>>arr[x];
sort(arr,arr+2*n);
rep(x,0,n) cout<<arr[x]<<" "<<arr[x+n]<<" ";
cout<<endl;
}
}
[(lambda n: (lambda arr : [print(f'{arr[i]} {arr[i+n]}', end = ' \n'[i==n-1]) for i in range(n)])(sorted(list(map(int,input().split())))))(int(input())) for _ in range(int(input()))]
1526B - I Hate 1111
Setter: errorgorn
Preparer: errorgorn
Read the name of the problem ;)
$$$1111=11 \cdot 101$$$
All numbers other than $$$11$$$ and $$$111$$$ are useless.
Method 1
Notice that $$$1111=11 \cdot 100+11$$$ and similarly $$$11111=111 \cdot 100 + 11$$$. This implies that we can construct $$$1111$$$ and all bigger numbers using only $$$11$$$ and $$$111$$$. So it suffices to check whether we can construct $$$X$$$ from $$$11$$$ and $$$111$$$ only.
Suppose $$$X=A \cdot 11 + B \cdot 111$$$, where $$$A,B \geq 0$$$. Suppose $$$B=C \cdot 11 + D$$$, where $$$D < 11$$$. Then $$$X=(A+C \cdot 111) \cdot 11 + D \cdot 111$$$. So we can just brute force all $$$11$$$ value of $$$D$$$ to check whether $$$X$$$ can be made.
Method 2
Since $$$\gcd(11,111)=1$$$, by the Chicken McNugget Theorem, all numbers greater than $$$1099$$$ can be written as a sum of $$$11$$$ and $$$111$$$. We can use brute force to find the answer to all values less than or equal to $$$1099$$$ and answer yes for all other numbers.
//雪花飄飄北風嘯嘯
//天地一片蒼茫
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <ext/rope>
using namespace std;
using namespace __gnu_pbds;
using namespace __gnu_cxx;
#define ll long long
#define ii pair<ll,ll>
#define iii pair<ii,ll>
#define fi first
#define se second
#define endl '\n'
#define debug(x) cout << #x << " is " << x << endl
#define pub push_back
#define pob pop_back
#define puf push_front
#define pof pop_front
#define lb lower_bound
#define ub upper_bound
#define rep(x,start,end) for(auto x=(start)-((start)>(end));x!=(end)-((start)>(end));((start)<(end)?x++:x--))
#define all(x) (x).begin(),(x).end()
#define sz(x) (int)(x).size()
#define indexed_set tree<ll,null_type,less<ll>,rb_tree_tag,tree_order_statistics_node_update>
//change less to less_equal for non distinct pbds, but erase will bug
mt19937 rng(chrono::system_clock::now().time_since_epoch().count());
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin.exceptions(ios::badbit | ios::failbit);
int TC;
cin>>TC;
while (TC--){
int n;
cin>>n;
rep(x,0,20){
if (n%11==0){
cout<<"YES"<<endl;
goto done;
}
n-=111;
if (n<0) break;
}
cout<<"NO"<<endl;
done:;
}
}
[(lambda n : print("YES" if (n >= 111*(n%11)) else "NO"))(int(input())) for _ in range(int(input()))]
1526C1 - Potions (Easy Version) and 1526C2 - Potions (Hard Version)
Setter: errorgorn and oolimry
Preparer: oolimry
Try dp!
The dp states are position and number of potions drank.
Speedup dp or use greedy for full solution.
Method 1 — DP
Let's consider a dynamic programming solution. Let $$$dp[i][k]$$$ be the maximum possible health achievable if we consider only the first $$$i$$$ potions, and $$$k$$$ is the total number of potions taken.
The transition is as follows: $$$dp[i][k] = max(dp[i-1][k-1] + a_i, dp[i-1][k])$$$ if $$$dp[i-1][k-1] + a_i \geq 0$$$, and just $$$dp[i-1][k]$$$ otherwise. The first term represents the case if we take potion $$$i$$$ and the second term is when we ignore potion $$$i$$$.
This runs in $$$O(n^2)$$$ and passes the easy version.
Method 2 — Greedy 1
We iterate through the potions in non-decreasing order and drink the potion if we do not die.
For convenience, we define $$$c_i=a_i+i \cdot \epsilon$$$, where $$$\epsilon$$$ is a very small real number so that we can treat $$$c_i$$$ as distinct integers. We will show by exchange argument that our greedy is optimal.
Let $$$S$$$ be the set of potions that is an optimal solution.
Suppose $$$i<j$$$ and $$$c_i<c_j$$$. If $$$i \in S$$$ and $$$j \notin S$$$, then removing $$$i$$$ and adding $$$j$$$ into $$$S$$$ will still make $$$S$$$ a valid solution.
Now, suppose that position $$$i$$$ is not drunk. We can assume that there are no $$$k$$$ ($$$k<i$$$) such that $$$c_k<c_i$$$ and $$$k$$$ is drunk by the previous assertion. Suppose we add $$$i$$$ into $$$S$$$. If we reach a position $$$j$$$ (we possibly die at $$$j$$$) where $$$c_j<c_i$$$, then we can remove $$$j$$$ from $$$S$$$ and add $$$i$$$ to $$$S$$$. Otherwise, our greedy will also not choose $$$i$$$, as it was not chosen when we only consider indexes $$$k$$$ such that $$$c_k<c_i$$$.
Notice that we can arbitrarily define the way $$$\epsilon$$$ is added, so basically we can process $$$a_i$$$ in any non-increasing fashion.
Doing this naively is $$$O(n^2)$$$ as well. However, using a range add range max lazy propagation segment tree, we can check if a certain potion can be drunk without dying, and the solution runs in $$$O(n \log n)$$$.
Method 3 — Greedy 2 / DP 2
We process the potions from left to right. At the same time, we maintain the list of potions we have taken so far. When processing potion $$$i$$$, if we can take $$$i$$$ without dying, then we take it. Otherwise, if the most negative potion we've taken is more negative than potion $$$i$$$, then we can swap out potion $$$i$$$ for that potion. To find the most negative potion we've taken, we can maintain the values of all potions in a minimum priority_queue. This runs in $$$O(nlogn)$$$ as well
To prove that this works, let's consider best solution where we take exactly $$$k$$$ potions (best as in max total health). The solution involves taking the $$$k$$$ largest values in our priority queue. Then when considering a new potion, we should see whether swapping out the new potion for the $k$th largest potion will improve the answer.
Since the priority queue is strictly decreasing, there will be a cutoff $$$K$$$, where for $$$k$$$ at most $$$K$$$, the answer is not affected, and for larger than $$$K$$$, we swap out the $$$k$$$th largest potion. It turns out this process is equivalent to inserting the new potion's value into the priority_queue. For those positions at most $$$K$$$, they are not affected. For the positions larger than $$$K$$$, the elements get pushed back one space, meaning that the smallest element is undrinked.
This can also be seen as an efficient way to to transition from one layer of the $$$dp$$$ table to the next.
#include <bits/stdc++.h>
using namespace std;
typedef pair<long long, long long> ii;
struct node{
int s, e, m;
long long val = 0; long long lazy = 0;
node *l, *r;
node(int S, int E){
s = S, e = E, m = (s+e)/2;
if(s != e){
l = new node(s, m);
r = new node(m+1, e);
}
}
void apply(long long L){
val += L;
lazy += L;
}
void push(){
if(s == e) return;
l->apply(lazy);
r->apply(lazy);
lazy = 0;
}
void update(int S, int E, long long L){
push();
if(s == S && E == e){
apply(L);
return;
}
else if(E <= m) l->update(S, E, L);
else if(S >= m+1) r->update(S, E, L);
else l->update(S, m, L), r->update(m+1, E, L);
val = min(l->val, r->val);
}
long long query(int S, int E){
push();
if(s == S && E == e) return val;
else if(E <= m) return l->query(S, E);
else if(S >= m+1) return r->query(S, E);
else return min(l->query(S, m), r->query(m+1, E));
}
} *root;
int main(){
ios_base::sync_with_stdio(false); cin.tie(0);
int n; cin >> n;
ii arr[n];
for(int i = 0;i < n;i++){
cin >> arr[i].first;
arr[i].second = i;
}
sort(arr,arr+n);
reverse(arr,arr+n);
int ans = 0;
root = new node(0, n-1);
for(int i = 0;i < n;i++){
int pos = arr[i].second;
long long x = arr[i].first;
if(x + root->query(pos,n-1) >= 0){
ans++;
root->update(pos,n-1,x);
}
}
cout << ans;
}
#include <bits/stdc++.h>
using namespace std;
int main(){
ios_base::sync_with_stdio(false); cin.tie(0);
int n; cin >> n;
priority_queue<long long, vector<long long>, greater<long long> > pq;
long long S = 0;
for(int i = 1;i <= n;i++){
long long x; cin >> x;
S += x;
pq.push(x);
while(S < 0){
S -= pq.top();
pq.pop();
}
}
cout << (int) pq.size();
}
import heapq
H = []
n=int(input())
for i in list(map(int,input().split())):
tot = (tot+i if 'tot' in locals() or 'tot' in globals() else i)
tot -= ((heapq.heappush(H,i) if tot >= 0 else heapq.heappushpop(H,i)) or 0)
print(len(H))
1526D - Kill Anton
Setter: errorgorn
Preparer: errorgorn
The time it takes for Anton's body to revert the string is related to inversion number.
We claim that in the optimal answer all characters of some type will appear consecutively.
Consider the character at position $$$i$$$ in string $$$s$$$. We define $$$C_i$$$ as the position in which that character will be in string $$$t$$$. For $$$s=\texttt{CAGCAA}$$$ and $$$t=\texttt{AAGCAC}$$$, $$$C={4,1,3,6,2,5}$$$. Then the minimum number of moves to transformed $$$s$$$ to $$$t$$$ is given by the inversion index of $$$C$$$.
Suppose we find a substring of $$$s$$$ where it is $$$\texttt{XXAA...AA[A]XX...XX[A]AA...AAXX}$$$, where characters $$$\texttt{X}$$$ can be either one of $$$\texttt{TCG}$$$. The square brackets are just for clarity of explanation. We will show that it our solution will not be worse if we merge these $$$2$$$ contiguous segments of $$$\texttt{A}$$$.
Consider transforming the string into $$$\texttt{XXAA...AAXX...XX[A][A]AA...AAXX}$$$ and $$$\texttt{XXAA...AA[A][A]XX...XXAA...AAXX}$$$. Let the difference in the number of moves be $$$D_1$$$ and $$$D_2$$$ respectively. And let the index of $$$\texttt{[A]}$$$s be $$$i$$$ and $$$j$$$ respectively.
Then $$$D_1=\sum\limits_{k=i+1}^{j-1} \sigma(C_k-C_i)$$$ and $$$D_2=\sum\limits_{k=i+1}^{j-1} \sigma(C_j-C_k)$$$, where $$$\sigma(x)=\frac{x}{|x|}$$$, or rather $$$\sigma$$$ is the sign function.
I claim that $$$D_1+D_2 \geq 0$$$. Suppose that $$$D_1+D_2<0$$$, then there exist $$$k$$$ such that $$$\sigma(C_k-C_i)+\sigma(C_j-C_k)<0$$$ which implies $$$C_k-C_i<0$$$ and $$$C_j-C_k<0$$$. However, this implies that $$$C_j<C_i$$$ which is clearly a contradiction.
Since $$$D_1+D_2 \geq 0$$$, either $$$D_1 \geq 0$$$ or $$$D_2 \geq 0$$$. WLOG, $$$D_1 \geq 0$$$. This implies that we turn $$$s$$$ into $$$\texttt{XXAA...AAXX...XX[A][A]AA...AAXX}$$$ without decreasing the number of moves to transform $$$s$$$ into $$$t$$$. Now, consider the rest of the $$$\texttt{A}$$$ on the left segment of $$$\texttt{A}$$$. We can move it too the right also. Recall that $$$D_1 + D_2 \geq 0$$$. In this case, we know that $$$D_2 \leq 0$$$ as it is the cost to move the left $$$\texttt{[A]}$$$ back to its original position. So $$$D_1 \geq 0$$$. Therefore, we have merged $$$2$$$ different segments of $$$A$$$ without decreasing the number of moves to transform $$$s$$$ into $$$t$$$.
So, we can try all $$$24$$$ possible strings and check the number of moves Anton's body needs to transform each string. The time limit is relaxed enough for a $$$O(n \log n)$$$ similar to 1430E - String Reversal.
But there is a $$$O(n)$$$ solution, the number of moves Anton's body needs to transform each string is given by the number of inversions in the string. But since we know that we only care about strings that have all the same characters appear consecutively, we can just keep a count of the number of inversions for each pair of characters.
//雪花飄飄北風嘯嘯
//天地一片蒼茫
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <ext/rope>
using namespace std;
using namespace __gnu_pbds;
using namespace __gnu_cxx;
#define ll long long
#define ii pair<ll,ll>
#define iii pair<ii,ll>
#define fi first
#define se second
#define endl '\n'
#define debug(x) cout << #x << " is " << x << endl
#define pub push_back
#define pob pop_back
#define puf push_front
#define pof pop_front
#define lb lower_bound
#define ub upper_bound
#define rep(x,start,end) for(auto x=(start)-((start)>(end));x!=(end)-((start)>(end));((start)<(end)?x++:x--))
#define all(x) (x).begin(),(x).end()
#define sz(x) (int)(x).size()
#define indexed_set tree<ll,null_type,less<ll>,rb_tree_tag,tree_order_statistics_node_update>
//change less to less_equal for non distinct pbds, but erase will bug
mt19937 rng(chrono::system_clock::now().time_since_epoch().count());
int n;
string s;
int cnt[4];
ll flips[4][4];
map<char,int> id={{'A',0},{'N',1},{'O',2},{'T',3}};
string cset="ANOT";
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin.exceptions(ios::badbit | ios::failbit);
int TC;
cin>>TC;
while (TC--){
cin>>s;
n=sz(s);
memset(cnt,0,sizeof(cnt));
memset(flips,0,sizeof(flips));
rep(x,0,n){
cnt[id[s[x]]]++;
}
rep(a,0,4){
int curr=0;
rep(x,0,n){
flips[a][id[s[x]]]+=curr;
if (id[s[x]]==a) curr++;
}
}
ll best=-1;
vector<int> ans;
vector<int> v={0,1,2,3};
do{
ll curr=0;
rep(x,0,4){
rep(y,x+1,4){
curr+=flips[v[y]][v[x]];
}
}
if (curr>best){
best=curr;
ans=v;
}
} while (next_permutation(all(v)));
for (auto &it:ans) rep(x,0,cnt[it]) cout<<cset[it];
cout<<endl;
}
}
import itertools
TC=int(input())
m={"A":0,"N":1,"O":2,"T":3}
st="ANOT"
for _ in range(TC):
s=input()
arr=[]
for ch in s:
arr.append(m[ch])
cnt=[[0,0,0,0],[0,0,0,0],[0,0,0,0],[0,0,0,0]]
cnt1=[0,0,0,0]
for i in arr:
for j in range(4):
cnt[j][i]+=cnt1[j]
cnt1[i]+=1
val=-1
best=[]
for perm in itertools.permutations([0,1,2,3]):
curr=0
for i in range(4):
for j in range(i+1,4):
curr+=cnt[perm[j]][perm[i]]
if (curr>val):
val=curr
best=perm
for i in range(4):
for j in range(cnt1[best[i]]): print(st[best[i]],end="")
print()
1526E - Oolimry and Suffix Array
Setter: iLoveIOI
Preparer: iLoveIOI
Try to solve the problem of the minimal $$$K$$$ needed to make a string with such a suffix array.
First, let's consider a simpler problem.
Is it possible to make a string with a certain suffix array given an alphabet size $$$k$$$.
Consider two adjacent suffixes in the suffix array "xy" and "ab" where $$$b$$$ and $$$y$$$ are some strings and $$$x$$$ and $$$a$$$ are some characters i.e. $$$x$$$ is the first character of that suffix and similarly for $$$a$$$. If $$$b$$$ and $$$y$$$ don't exist we consider them as \$, i.e. smaller than everything. Also, "xy" comes before "ab".
Observation: If the position of $$$b$$$ is less than the position of $$$y$$$ in the suffix array, $$$x$$$ must be less than $$$a$$$. Otherwise, $$$x$$$ must be less than or equal to $$$a$$$.
This can be easily shown as "xy" must be lexicographically smaller than "ab". This is sufficient also.
Thus we can iterate through the suffix array and check if $$$pos[arr[i]+1]>pos[arr[i+1]+1]$$$ where $$$arr$$$ is the suffix array and $$$pos$$$ is the position of the $$$i$$$th element in the suffix array. If this condition holds then the $$$arr[i]$$$ th character must be strictly less than the $$$arr[i+1]$$$ th character. Thus we can just count how many such pairs exist. If this count is larger than the alphabet size no such string is possible. Otherwise, such string exists. Note that special care must be taken when considering $$$arr[i]=n-1$$$ as $$$pos[n]$$$ may not be defined ($$$0$$$-indexed).
After tackling the simpler question we move on to the full question of counting how many such strings are there. If we consider the string as an array and the order of the array as the order of the suffix array meaning that the $$$i$$$ th element of this array is the $$$arr[i]$$$ th element of the string. We have now transformed the question into "Given that some elements must be greater than the previous elements while others can be equal. Count how many arrays are there such that the largest element is less than $$$k$$$".
Consider the difference array, some elements must be $$$\geq 1$$$ while some can be $$$\geq 0$$$. We add padding to the front and back of the array so as to account for the first value being non-zero and the last element being less than $$$k$$$. These two elements are both $$$\geq 0$$$. Let $$$cnt$$$ be the number of elements that must be $$$\geq 1$$$ in the difference array. Now, this becomes count how many arrays of $$$(n-1+2)=(n+1)$$$ non-negative elements sum to $$$k-cnt$$$. This can be solved using stars and bars so the final answer comes out to be $$$n+1+k-cnt \choose n$$$ which can be found easily. Note that we define $$$\binom{a}{b}=0$$$ when $$$a<b$$$.
Final Complexity $$$O(n\log MOD)$$$ or $$$O(n)$$$ depending on how you find the modular inverse.
Btw $$$k$$$ was chosen to also be $$$\leq 2\times 10^5$$$ so as to hide the final complexity :)
/*input
5 4
3 4 2 1 0
*/
#include<bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
using namespace std;
using namespace __gnu_pbds;
typedef tree<long long, null_type, less_equal<long long>, rb_tree_tag, tree_order_statistics_node_update> indexed_set;
//order_of_key #of elements less than x
// find_by_order kth element
typedef long long int ll;
#define ld long double
#define pii pair<ll,ll>
#define f first
#define s second
#define pb push_back
#define REP(i,n) for(ll i=0;i<n;i++)
#define REP1(i,n) for(int i=1;i<=n;i++)
#define FILL(n,x) memset(n,x,sizeof(n))
#define ALL(_a) _a.begin(),_a.end()
#define sz(x) (int)x.size()
const ll maxn=2e5+5;
const ll maxlg=__lg(maxn)+2;
const ll INF64=4e17;
const int INF=0x3f3f3f3f;
const ll MOD=998244353;
const ld PI=acos(-1);
const ld eps=1e-9;
#define lowb(x) x&(-x)
#define MNTO(x,y) x=min(x,(__typeof__(x))y)
#define MXTO(x,y) x=max(x,(__typeof__(x))y)
#define SORT_UNIQUE(c) (sort(c.begin(),c.end()), c.resize(distance(c.begin(),unique(c.begin(),c.end()))))
ll mult(ll a,ll b){
return ((a%MOD)*(b%MOD))%MOD;
}
ll mypow(ll a,ll b){
if(b<=0) return 1;
if(a<=0) return 0;
ll res=1LL;
while(b){
if(b&1) res=mult(res,a);
a=mult(a,a);
b>>=1;
}
return res;
}
int arr[maxn],pos[maxn];
ll inv(ll x){
return mypow(x,MOD-2);
}
int32_t main(){
ios::sync_with_stdio(false),cin.tie(0);
int n,k;
cin>>n>>k;
--k;
REP(i,n) cin>>arr[i],pos[arr[i]]=i;
pos[n]=-1;
int cnt=0;
REP(i,n-1){
// character at arr[i] and arr[i+1] cannot be the same
if(pos[arr[i]+1]>pos[arr[i+1]+1]){
++cnt;
}
}
//calculate c(k-cnt+n+1-1,n+1-1)
k-=cnt;
if(k<0){
cout<<0;
return 0;
}
ll ans=1;
REP1(i,n){
ans=mult(ans,inv(i));
ans=mult(ans,(k+i));
}
cout<<ans;
}
MOD=998244353
n,k=map(int,input().split())
arr=list(map(int,input().split()))
pos=[0]*(n+1)
for i in range(n):
pos[arr[i]]=i
pos[n]=-1
cnt=0
for i in range(n-1):
if (pos[arr[i]+1]>pos[arr[i+1]+1]): cnt+=1
#k-cnt+n-1 choose n
num,denom=1,1
for i in range(n):
num=num*(k-cnt+n-1-i)%MOD
denom=denom*(i+1)%MOD
print(num*pow(denom,MOD-2,MOD)%MOD)
1526F - Median Queries
Setter: errorgorn and oolimry
Preparer: errorgorn
Find elements $$$1$$$ and $$$2$$$ in $$$N+420$$$ queries.
Find a pair $$$(a,b)$$$ such that $$$|p[b]-p[a]| \leq \frac{n}{3}-c$$$, where $$$c$$$ is some constant.
The problem can be broken into $$$2$$$ main parts:
- Finding a pair $$$(a,b)$$$ such that $$$|p[a]-p[b]|$$$ is roughly less than a third.
- Finding elements $$$1$$$ and $$$2$$$ (actually we may find $$$N$$$ and $$$N-1$$$ but it is the same).
- Find the rest of the elements
A convenient way to think about the queries, is that given $$$p[a]<p[b]<p[c]$$$, we will be returned $$$\max(p[b]-p[a],p[c]-p[b])$$$.
We will spend the first queries to find a tuple $$$(a,b,c)$$$ such that the return value of this query is at most $$$\lfloor \frac{n-4}{6} \rfloor$$$. The easiest way to do this is by randomly choosing distinct $$$a$$$,$$$b$$$,$$$c$$$ and querying it. See proof 1 for the random analysis. But there is also a deterministic solution. Choose any $$$13$$$ elements from the array, and it is guaranteed that there exists a tuple in those $$$13$$$ elements such that the return value of the query is at most $$$\lfloor \frac{n-4}{6} \rfloor$$$, see proof 2. To query all tuples in this sub-array of size $$$13$$$, it takes $$$286$$$ queries, which fits very comfortably under $$$420$$$. user14767553 conjectured that a sub-array of size $$$10$$$ works, however we are unable to prove it. You can try to hack his solution at 117685511.
Among $$$a$$$, $$$b$$$, and $$$c$$$, we choose $$$a$$$ and $$$b$$$. The important idea here is that the gap between $$$a$$$ and $$$b$$$ is small, because we have found a tuple $$$(a,b,c)$$$ is less than or equal to $$$\lfloor \frac{n-4}{6} \rfloor$$$, so $$$|p[a]-p[b]| \leq 2 \cdot \lfloor \frac{n-4}{6} \rfloor \leq \lfloor \frac{n-4}{3} \rfloor$$$. Now, we query all tuples $$$(a,b,x)$$$ for all $$$x \ne a$$$ and $$$x \ne b$$$. Since the gap between $$$a$$$ and $$$b$$$ is small, we should be able to identify either $$$(1,2)$$$ or $$$(n,n-1)$$$. This is because either $$$p[a]-1 > p[b]-p[a]$$$ or $$$n-p[b] > p[b] - p[a]$$$ (WLOG assuming $$$p[b] > p[a]$$$), see proof 3. Therefore, the furthest $$$x$$$ will return the largest value when querying for $$$(a,b,x)$$$. (If there's ties choose anyone).
Suppose we found element $$$1$$$, there are at most two possible candidates for element $$$2$$$, $$$y_1$$$ and $$$y_2$$$ (the other possible candidate will be either $$$n$$$ or $$$n-1$$$). We can use 2 queries to figure out which of them is element $$$2$$$. We can query $$$(1, y_1, a)$$$ and $$$(1, y_2, a)$$$. Whichever produces the smaller value is element $$$2$$$, see proof 4.
Once we have found elements $$$1$$$ and $$$2$$$, solving the rest of the problem is simple. Querying $$$(1,2,x)$$$ will always return $$$x-2$$$. And we can find the rest of the elements in another $$$n-2$$$ queries. Do not forgot about the condition that $$$p[0]<p[1]$$$!
This is a rough asymptotic analysis for large $$$n$$$.
Observe that if
- $$$\frac n6 < b < \frac{5n}{6}$$$ (this happens around $$$\frac 23$$$ of the time)
- $$$b-\frac{n}{6} < a < b$$$ (around $$$\frac 16$$$ of the time)
- $$$b < c < b+\frac{n}{6}$$$ (around $$$\frac 1 6$$$ of the time)
Around $$$\frac{1}{54}$$$, we will get a return value of less than $$$\frac{1}{6}$$$. Since there are 6 permutations (i.e. relative orderings of a,b,c), there is a probability of roughly $$$\frac{1}{9}$$$ that some permutation of $$$(a,b,c)$$$ satisfies the above condition.
The probability that we do not find such a tuple after $$$420$$$ queries is $$$(\frac{8}{9})^{420} \approx 3.28\cdot10^{-22}$$$. To put this into perspective, you have a higher chance of:
- Flipping heads $$$70$$$ times in a row
- Drawing a royal flush $$$5$$$ times in a row
- Anton not rejecting a data structure problem
We will use contradiction.
let $$$d1, d2, \ldots ...$$$ refer to the gaps between the elements. If the maximum any two consecutive gaps is at most $$$\lfloor \frac{n-4}{6} \rfloor$$$, one of the queries will work. As such, it is necessary that least $$$6$$$ of these gaps are at least $$$\lfloor \frac{n-4}{6} \rfloor$$$.
Then we have $$$6 \cdot (\lfloor \frac{n-4}{6} \rfloor+1) +13$$$ as the smallest possible size of the original array.
However, $$$6 \cdot (\lfloor \frac{n-4}{6} \rfloor+1) +13 \geq 6 \cdot (\frac{n-9}{6}+1) +13 = n+10$$$ which is a clear contradiction.
We proof this statement by contrapositive.
This statement is equivalent to: if $$$a-1 \leq b-a$$$ and $$$n-b \leq b-a$$$, then $$$b-a > \lfloor \frac{n-4}{3} \rfloor$$$. Abbreviating $$$p[a]$$$ and $$$p[b]$$$ to $$$a$$$ and $$$b$$$ respectively.
Using algebra, $$$a-1 \leq b-a$$$ implies $$$2a -1 \leq b$$$ and $$$n+a \leq 2b$$$.
Therefore, $$$n+3a-1 \leq 3b$$$.
Then, $$$\frac{n-1}{3} \leq b-a$$$.
It is trivial to see that $$$\lfloor \frac{n-4}{3} \rfloor < \frac{n-1}{3}$$$.
Therefore, we have shown that $$$b-a > \lfloor \frac{n-4}{3} \rfloor$$$.
Suppose that $$$y_1=2$$$ and $$$y_2 = n-1$$$ or $$$y_2=n$$$. We can bound $$$a$$$ by $$$y_1 < a < y_2$$$
We want to show that the query of $$$(1,y_1,a)$$$ is smaller than $$$(1,a,y_2)$$$.
This is equivalent to showing that $$$\max(|1-2|,|2-a|) < \max (|1-a|,|a-y_2|)$$$.
Since $$$2 < a$$$, $$$\max(|1-2|,|2-a|)=a-2$$$.
Case $$$1$$$: $$$|1-a| \geq |a-y_2|$$$
$$$\max(|1-a|,|a-y_2|)=a-1$$$.
Therefore, $$$\max(|1-2|,|2-a|) = a-2 < a-1 = \max(|1-a|,|a-y_2|)$$$.
Case $$$2$$$: $$$|a-y_2| > |1-a|$$$
$$$\max(|1-a|,|a-y_2|)=|a-y_2|$$$.
Therefore, $$$\max(|1-2|,|2-a|) = a-2 < a-1 = |1-a| < |a-y_2| = \max(|1-a|,|a-y_2|)$$$.
//雪花飄飄北風嘯嘯
//天地一片蒼茫
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <ext/rope>
using namespace std;
using namespace __gnu_pbds;
using namespace __gnu_cxx;
#define ll long long
#define ii pair<ll,ll>
#define iii pair<ii,ll>
#define fi first
#define se second
#define debug(x) cout << #x << " is " << x << endl
#define pub push_back
#define pob pop_back
#define puf push_front
#define pof pop_front
#define lb lower_bound
#define up upper_bound
#define rep(x,start,end) for(auto x=(start)-((start)>(end));x!=(end)-((start)>(end));((start)<(end)?x++:x--))
#define all(x) (x).begin(),(x).end()
#define sz(x) (int)(x).size()
#define indexed_set tree<ll,null_type,less<ll>,rb_tree_tag,tree_order_statistics_node_update>
//change less to less_equal for non distinct pbds, but erase will bug
mt19937 rng(177013);
int query(int a,int b,int c){
cout<<"? "<<a<<" "<<b<<" "<<c<<endl;
int temp;
cin>>temp;
return temp;
}
void sort(int &a,int &b,int &c){
if (a>b) swap(a,b);
if (b>c) swap(b,c);
if (a>b) swap(a,b);
}
void solve(){
int n;
cin>>n;
vector<int> ans(n+5,0);
set<tuple<int,int,int> > s;
int a,b,c;
rep(x,1,14) rep(y,x+1,14) rep(z,y+1,14){
if (query(x,y,z)<=(n-4)/6){
a=x,b=y,c=z;
break;
}
}
map<int,vector<int>,greater<int> > m;
rep(x,1,n+1) if (x!=a && x!=b){
m[query(a,b,x)].push_back(x);
}
int hv=(*m.begin()).fi;
if (sz(m[hv-1])>=2){ //there must be exactly 2
if (query(m[hv][0],m[hv-1][0],a)>
query(m[hv][0],m[hv-1][1],a))
swap(m[hv-1][0],m[hv-1][1]);
}
int hi=m[hv][0],hi2=m[hv-1][0];
//cout<<hi2<<" "<<hi<<endl;
ans[hi]=1,ans[hi2]=2;
rep(x,1,n+1) if (x!=hi2 && x!=hi){
ans[x]=query(hi,hi2,x)+2;
}
if (ans[1]>ans[2]) rep(x,1,n+1) ans[x]=n-ans[x]+1;
cout<<"! "; rep(x,1,n+1) cout<<ans[x]<<" "; cout<<endl;
cin>>n; //read stupid value
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin.exceptions(ios::badbit | ios::failbit);
int TC;
cin>>TC;
while (TC--){
solve();
}
}
import sys, random
print = sys.stdout.write
input = sys.stdin.readline
def query(a, b, c):
print("? " + str(a+1) + " " + str(b+1) + " " + str(c+1) + "\n")
sys.stdout.flush()
return int(input())
def answer():
print("! " + " ".join([str(i) for i in ans]) + "\n")
sys.stdout.flush()
return int(input())
T = int(input())
testVal = 13
randomQueryOrder = []
for i in range(testVal):
for j in range(i+1, testVal):
for k in range(j+1, testVal):
randomQueryOrder.append((i, j, k))
for caseno in range(T):
N = int(input())
a = -1
b = -1
ans = [0 for i in range(N)]
res = [0 for i in range(N)]
order = [i for i in range(N)]
minVal = N+5
random.shuffle(order)
random.shuffle(randomQueryOrder)
for ijk in randomQueryOrder:
i, j, k = ijk
i = order[i]
j = order[j]
k = order[k]
temp = query(i, j, k)
if temp <= (N-4)//6:
a = i
b = j
break
assert(a != -1 and b != -1)
''' Now, the key thing to note is that abs(P[a]-P[b]) is less than (roughly speaking) N/3.
Observe that the index c such that query(a, b, c) is maximum must be such that P[c] == 1 or P[c] == N (some steps skipped).
But given the condition P[1] < P[2], we can assume either, then flip using P[i] = N+1-P[i] if condition not satisfied.
'''
# Now, we assume P[c] = 1
# There always exists another index d such that query(a, b, d) = query(a, b, c)-1 and P[d] = 2
# There can be only at most 2 d which satisfy the former, and we can check which is which by comparing query(a, c, d)
maxVal = -1
c = -1
for i in range(N):
if a == i or b == i:
continue
res[i] = query(a, b, i)
if res[i] > maxVal:
maxVal = res[i]
c = i
d2 = []
for i in range(N):
if a == i or b == i:
continue
if res[i] == maxVal-1:
d2.append(i)
d = -1
if len(d2) == 1:
d = d2[0]
elif len(d2) == 2:
temp1 = query(a, c, d2[0])
temp2 = query(a, c, d2[1])
if temp1 < temp2:
d = d2[0]
else:
d = d2[1]
else:
assert(False)
# After finding indices c and d such P[c] = 1 and P[d] = 2, we can now find the rest of the values
ans[c] = 1
ans[d] = 2
for i in range(N):
if i == c or i == d:
continue
ans[i] = 2 + query(c, d, i)
# Flip since P[1] < P[2] not satisfied
if ans[0] >= ans[1]:
for i in range(N):
ans[i] = N+1-ans[i]
result = answer()
# I dislike getting WA, hence I make my code MLE
if result != 1:
MLE = [1 for i in range(1<<27)]
sys.stdout.write(MLE[0])
Code Golf
You may have realized that python codes in the editorial are quite short. We actually had a code golf challenge among testers. You are invited to try code golf our problems and put them in the comments. Maybe I will put the shortest codes in the editorial ;)
Rules for code golf:
- any language allowed
- codes will be judged by number of characters
- must get AC in the respective problems










ERRORGORN OFZ
I wish they were BUGABOO's so that I can solve them.
QUESTIONS are really hard to ANSWER :")
When the problemsetters have plans for the night:
Source: 1526B - I Hate 1111
nice
If that was the case , then answer for it should be "YES"...lol
Sadly for him the answer for the test case "69" was "NO".
speedforces :)
It was more about how fast you come to solution and not how fast you type. Code for first 4 tasks were short.
He is talking about how fast the editorial came.
I seriously hate 1111 after this contest.
I even tried Dynamic programming for multiple times. But the constrain of 10^9 killed me badly :(
You just need to use brute force to see that a number bigger than 1000~2000 will always return true, also bigger than 2000 always be true. So you can only use DP to find in a very small range, not 1e9 range :)
good job :)
Excellent! Thanks a lot! I cannot express to you how glad I am after getting accepted the B with Dynamic Programming! I just put a condition that any number greater than 1500 will be "YES". And Woo ! It got accepted.
Here is the DP Solution for Problem B
bro please give me itterative dp solution if possible
Simple Iterative DP
why every number greater than 1099 is possible to make with this condition?
Did not see solution to A.
Edit: Which is a shame because I solved B and and both C correctly.
You could random shuffle the array until it becomes good. Though it makes the code longer (not that much longer), it's a nice alternative to the proposed solution.
Actually I thought about that, but was not able to aproximate the probability that it works.
It is going to take a lot of time.
Let the number of all permutation of the 2*n elements be p=50!, without the rotations counted double it is p=49!
So, how much of these p permutations qualify as "no solution" in the worst case? What is the expected number of shuffles until we find a good solution?
It seems obvious that we got the most "no solution" permutations if the array is an arithmetic sequence, so WLG lets assume it is 1,2,3...,n
Consider the third element, it must not be one of n-2, because all other of the n-2 elements produce a good solution. Same for the next element... and so on.
So one aproximation to get a good perm looks like $$$(n-2)/(n-1) * (n-3)/(n-2) * (n-4)/(n-3) * ... $$$
This formular is a of course a simplyfication and kind of simply wrong, however, it yields an propabilty of ~0.04, ie an expected value of ~25 shuffles until we find a good permutation.
You could have solved A later and maybe then you would have got the idea. I usually solve problems in order, but I was not sure of my solution to A (though it was right), then moved to B which again I failed to solve. I opened C1,C2 and was able to solve them fast. Then returned to A and then to B.
In A i sorted the elements first say for example 1 2 3 4 5 6 and arranged them like 1 6 2 5 3 4.
Well, I've gotten used to thinking twice before submitting the first time.
When I cannot solve A this means at some point of time I solved B, then have to decide, do I really want to participate with this? I am late, I have no solution to A.
Most likely the answer is simply no, at least for me. In this contest, it turns out I would have had a positive delta even without solving A. But that is usually not the case.
I would have to overcome this "rating-thinking", which would actually be good on a rational level, because it really doesn't matter whether I'm 1500 or 1600. But the point is still difficult for me.
It does feels bad when i lose rating but i don't skip if i don't get any solution for 40 minutes (happened in this contest). As long as we don't cross our highest rating, any rating below it will be temporary.
11 and 1 are enough as 111=11*10+1
if the below condition satisfies, its YES
11*a+1*b=n and a>=b*10;
code : https://mirror.codeforces.com/contest/1526/submission/117686801
despite bricking the round, i enjoyed it. thanks for the amazing round!
Thanks the authurs for nice bugaboos statements and detail + quick solutions for those bugaboos
i've never seen so many memes in 1 editorial
i know everyone will downvote this but problem 2 is such a bad problem. CP problems should never be based one single tricky clue
i agree that it's tricky, but it's no different from any anton problem where the solution becomes trivial after finding a key observation
Why not?
because problems should be built on something that you know, so that you will deduce the unknown from the known. that’s the beauty of cf. I cannot just give you riddles in cf problems
Anyways that’s just my opinion. Feel free to ignore
Your opinion based only on solution in editorial? There are more others solutions with easy logic.
Please someone explain why in 2nd problem only 11 and 111 are useful. Thanks :|
you can express 11111 as 111*100 +11 and 1111 as 11 * 100 +11 and use a similar argument for all other numbers of the sort
let's call k times 1 as k-1. So 4-1, 6-1 and 8-1 could be made just by 2-11(1100 + 11, 110000 + 1100 + 11, 11000000 + 110000 + 1100 + 11). Further 5-1 and 7-1 can be made by 2-1 and 3-1 alone(11100 + 11, 1110000 + 1100 + 11) so instead of using 4-1, 5-1, 6-1, 7-1, 8-1 we can simply use 2-1 and 3-1 so we can ignore everything except 2-1 and 3-1.
will this be the fastest editorial of all time?
So we can just brute force all 11 value of D to check whether X can be made.but we would still have to find A and C to satisfy equation ?but this is a YES/NO.
If we find (A+C,D) then the answer is YES. we dont care about what A and C actually are.
I used random shuffle until the array is good :( (problem A)
Pls tell me how to improve my skills! I couldn't solve any problems in this contest. :(
first have decent knowledge of known algorithms, mathematics, number theory and probability. Then solve past problems. The last one is necessary
How in problem C1, the dp does not depend upon the actual potions taken? I mean, how can I calculate ans for dp[i][k] without knowing what is my current health?
Well put-together editorial!
feeling after the contest
Thanks for B.
Can anybody explain what is wrong in my solution for problem C1 div2(https://mirror.codeforces.com/contest/1526/submission/117651697)
Consider a multiset of integers: { 1 , 1 , 2 , 3 , 4 }
When you write this line : a.erase(*a.begin()); // or try to erase any occurrence of an element
It erases all the occurrences of that element. The multiset becomes : { 2 , 3 , 4 }
To avoid this, You can make use of iterators: auto it = a.begin(); a.erase(it); or you can use a.erase(a.begin());
The multiset now becomes : { 1 , 2 , 3 , 4 }
I hope you understand this simple issue with your code.
thnx man u really told a very good point! i was doing the very same mistake and was stuck on this since yesterday , thnx again !!
Vote if you hate 1111 too :(
Weird Idea for Problem A
Though the idea is not good, we can random_shuffle() the whole array for infinity times and check if it satisfies the condition at any moment.
(In this way, my problem A got accepted)
Yea... the array that cause this to fail with most probability is $$$1,2,3,4,\ldots$$$
Even then its like around 50% chance to fail...
C1 was easier than B for me even though I wasn't able to solve both
Brother can you please tell what is the error in my solution for C1(https://mirror.codeforces.com/contest/1526/submission/117651697).
This line:
s.erase(*s.begin());Erases all copies of the value of s.begin(). You can pass an iterator to s.erase so just replace it with
s.erase(s.begin());I tried Top Down DP approach for C1. Potions (Easy Version) but I got TLE on pretest-3. Here is my code. Can you tell me why I got TLE for this and what should be the optimal Top-Down DP Solution for the same?
Thanks in Advance :)
Put the code in the spoiler tag, it's annoying
What is spoiler tag? I don't know can you tell me about this?
It is written like this, without spaces, ofc.
< spoiler summary="some code" > some code... < /spolier >
You can also click the CF logo above the text box and see the spoiler thing.
For B, what about this simpler solution:
Consider $$$x=n \mod 11$$$ We need to use at least x times 111, so if $$$n>=111*x$$$ then there is a solution since $$$n-x*111=0 \mod 11$$$, else there is none.
Can you please explain how your solution works?
I mean the idea behind this solution. Thanks.
The idea is the same as in the editorial, a number that can be build by the rules of the problem can also be build as a sum of 11 and 111.
111%11==1 So we must use at least n%11 times a 111 to build n. This means n cannot be smaller than (n%11)*111. And we can build n by using (n%11)*111 + y*11 for some arbitray y.
117686327
n can be written as : n = q*11 + (n%11), let (n%11) = x.
I am not getting this line:
So we must use at least n%11 times a 111 to build n.
$$$(x*11 + 1*111) = 1 \mod 11$$$
$$$(x*11 + 2*111) = 2 \mod 11$$$
$$$(x*11 + 3*111) = 3 \mod 11$$$
...
Alternate solution to A: You can just sort the array and swap all elements by 1 on right except first and last elements
Oh no
You can drink Potion with 0, right? but the ans is not according to that, what's wrong in this code
Your solution is wrong. You are adding all the negative values at the end, which is not what the question is asking for.
For example, for the case
1 -2 1000if you add positives and then subtract negatives you will get
3as the answer. However, we cannot take-2, since that would decrease your running total to -1, which is not allowed.What is the base case for
1526C1,(Method 1)DP solution? Also, shouldn'tkincrease, if we are counting how many potions are we taking?dp[0][0] = 0
Love the way "You write editorial".
Problem D, I used cin, cout, unordered_map to solve and get TLE, change these to scanf, prinf and character to number and unordered_map to array and got AC.
Poor me!
wtf is Chicken McNugget and why on earth should one even know this sht????
It's an interesting theorem that has a rather remarkable statement, after a certain number, every number can be written in the form of ax + by (given a, b are coprime).
It is easy to understand once you know it, but it is not known/popular and thus a problem which intended to be easy (Problem B Div. 2) should not require these kinds of knowledge, but instead, it should require thinking.
In question C, why using upper_bound in multiset while substituting the ith number gives wrong answer but removing the last element does the trick?
How to solve C using dp ,please explain.
say dp[i][j] means max HP after reaching i_th glass and having drunk j health potions. For the transition we can say that dp[i][j] = max(dp[i-1][j](meaning we did not drink the i_th potion), dp[i-1][j-1]+a[i](meaning we did drink the i_th potion)). For base case dp[-1][-1] = 0.(Take care of the indexing :))))
Aren't we trying to maximize the number of potions we take, So in the dp why did we take dp[i][j] to be maximum health?
yeah, see the answer will be the max j for which dp[n-1][j] is non negative. We are trying to keep the track of max health that we can have after being on i_th potion and having drunk j potions. The reason for that is that in future we might have to drink potions that'll decrease the character's health and so it should be as high as possible right now to be able to drink those negative potions while remaining alive.
Easiest Solution.
`[contest:723][problem:B]
Put your codes in spoiler, please!
Problem B can be solved in a much simpler way, the given number (say x) will be of the form
x = a1 * 11 + a2 * 111since, 111 can be written as 11*10 + 1, we can obtain the value of a2 as,a2 = x % 11Then we can check if
x - a2*111is non-negative and divisible by 11.Actually you only need to check if it is non-negative.
Can anyone plz elaborate why 11*10 + 1 ensures that we can take value of a2 as x % 11 ?
Doing that, we can write the equation as
The equation takes the form,
a = b*q + rHence a2 will be remainder of x % 11Anton lived today, but I'll get him next time for sure.
Thanks for providing method 2 with
Chicken McNugget Theoremin solution B.For those who are interested in understanding the proof of correctness of this theorem can refer this resource
I used multiset in C1 and C2 instead of priority queue
Priority queue works faster than multiset, except for that they don't differ.
and, priority queues don't have iterators afaik
I meant in problem C.
I used segment tree with min() merge function! Your solution is much nicer though.
Please can you explain the segment tree aproach?The editorial was a bit difficult for me to understand.Thanks in advance.
You need to track the sum over the prefix [0, len]. Each time this sum dips below 0 you use segment tree to find the minimum value and the corresponding index. This is the one drink that we retroactively decide not to drink. Set it's value to zero in the tree and increase your sum (current health) by an appropriate amount. Repeat until your health is no longer negative. Move on to the next prefix. n*log(n) time. At least that's how I used it.
Thanks a lot .I think I got the basic idea.
I have some questions regarding the proof of D.
I think my solution on D should give TLE, but i can't prove it.
In my code, i did a 4! * (2^3) * N log N solution, and in first time i got TLE on pretest 5 . Basically the solution was: For any permutation of the 4 letters, try to rearrange the string by put the same letter together on the left or right side (well, that's not necessary cause im trying all the permutations, but i didnt realize) and then use FenwickTree to count inversion (same solution of editorial, but with *8 because of bitmask).
To avoid TLE i used a set that checks if the initially string miss some letter, in that case, i can avoid use some permutations. By doing that, i think the constant factor (4! * (2^3)) was reduced a little, but i think too that maybe in any worst case it shouldn't change. It passed from TLE on pretest5 to accepted with 970ms.
If anyone can find a case, or prove why using the set improves the code, it would be cool. Thanks.
memesforces.
Can anyone provide code/ intuition for the Merge Sort approach for bugaboo D?
I didn't solved because I didn't notice that there were only 4 characters , :( . But I had the intuition , see I observed that all the elements will be together by righting a few things down and verifying with sample test cases , then I thought there were 26! Permutation ( as I didn't read 4 chars , :( ) . So now if you would look at that there are just 24 permutations and for sure the solution will be one of those permutation , then for the merge sort technique it is a well known idea of that number of inversion = minimum no. Of adjacent swaps , and it could be solved using PBDS and Merge sort .
What's PBDS?
What was the intuition behind the elements would be together? @dhruv7888
The whole idea is that that it is a number of inversions, after that you just calculate inversions using mergesort, a standard trick.
You can look at my submission (yeah, I just copy-pasted merge sort from the internet if anything)
I think I don't understand why greedy for C2 works. I wonder can it not happen that one swap with the minimum in priority queue is not enough and we might need two swaps? Sure, it will decrease the number of potions for now, but it might happen that the potentially more positive value gained will help us take more negative potions in the future or something like that? And i am only talking about the case when after one swap our sum remained < 0, but after two swaps the sum became >= 0.
If the current element is -11 and you had -10 before as most negative element , then you will not remover , but if you had -11 before and now the current element is -10 then deleting -11 is enough you don't need to delete any more.
No I mean, if let's say our priority queue contains -7 and -5 . I just came across -11 and I can't take it as my sum becomes less than 0, so I check sum + 7 — 11 and it is negative still but if I also take 5, then it becomes sum + 7 + 5 — 11 which somehow comes out to be >= 0 , then isn't it optimal to remove both -7 and -5 and take the 11? Sure, the number of potions decreased but since our sum is now greater than earlier value and greater than 0, we might able to take more potions later on. Did I miss something? EDIT: I understood . Thanks :)
Can someone explain question B in very simple language to someone who suck at Cp..
The simplest solution:
All the given numbers mod 11 are 0 or 1.
Suppose X%11 is not zero, then we need to cancel this out. This needs at least 111*(X%11). So the one-line solution is (X>=111*X%11? "YES":"NO").
In the potions problem, why do we keep the number of potions taken till now as one of the states? I mean that is something that we need to calcuate right? Why do we include it in the states?
Problem C1 easy version: how ro solve this provlem using 1D dp
dp[i] = maximum health you can have with drinking exactly i potions in this level.
for i : 1 -> n: potions
for j : n -> 1: number of potions we want to drink if(dp[j - 1] + a[i] >= 0) dp[j] = max(dp[j], dp[j - 1] + a[i])Answer is the largest i, that we have a valid value for dp[i]
Can you explain a bit more why are you defining dp[i] as the "Maximum Health"?
Dp from editorial: "Let dp[i][k] be the maximum possible health achievable if we consider only the first i potions, and k is the total number of potions taken."
Just like what editorial have explained, but we wanna remove the part of "if we consider only the first i potions" and we will only have dp[k]. So now dp[i] = maximum health that can be achieved by taking i potions in this level (we will iterate over array of potions and "level" will be that). The only thing is we need to iterate over number of potions we wanna take form n to 1, since we need to update our dp from last level, so that if we are updating dp[i], we need dp[j] (for all j < i) to be just like the last level and haven't been updated yet.
submission.
segment tree in Div2 C seriously?
Well it was not a segment tree bugaboo though I solved it using it as well ( You can verify it from editorial they havent even mentioned it ).
However, using a range add range max lazy propagation segment tree, we can check if a certain potion can be drunk without dying
Yeah I did the same :)
For problem C2 "Method 2 — Greedy 1" can be implemented
without a lazy segment treeusing BIT:Maintain a set of positive potion positions, and a priority queue of {negative potion value, index}. Check if the negative potion can be consumed using BIT. Greedily start decrementing the potion value of positions in descending order of positions that are less than the index while exhausting the priority queue & remove the position from the set if potion value reaches zero.
UPD: It turns out that my previous submission (without BIT) gives TLE for this hack case since my worst-case time complexity was $$$\mathcal{O}(n^2\log{}n)$$$, after optimizing using BIT it reduces to $$$\mathcal{O}(n\log{}n)$$$.
Cheese submission: 117672658, Optimized submission: 117983932
There is a little difference of alphabet between D and editorial. It looks like DNAs initially and you modified it for your outstanding coordinator.
smallest and lovely solution for I Hate 1111 can be:-
as we know we have to check only for 11, 111 (from editorial),
And also 111 = 11*10 + 1, therefore equation reduces to x = (a+10*b)*11 + b
now b = x%11 and a + 10*b = x/11
The neat sol. can be found at :- https://mirror.codeforces.com/contest/1526/submission/117617666
Hope it helps ;)
Is the name Anton came from Silicon Valley series?
nope, its name of coordinator that reject a lot of problems
Can someone explain how they got the intuition for placing the same letters together in D?
Problem B was really nice and loved the editorial and the way solutions are given to the problems. Kudos to writers and testers!!
I loved I Hate 1111
what if in problem B there are 3 numbers left 11a+111b+(s)c=x how will we find if x can be made by adding any number of these 3 numbers 11,111,s ?
Read about Extended Euclidian and Linear Diophantine. CP-ALGO
I have another visual proof of the Chicken McNugget theorem (from problem B)
n = 5 and m = 7, so it can get all the numbers after 5*7-5-7 = 23
Here is the number line of 5's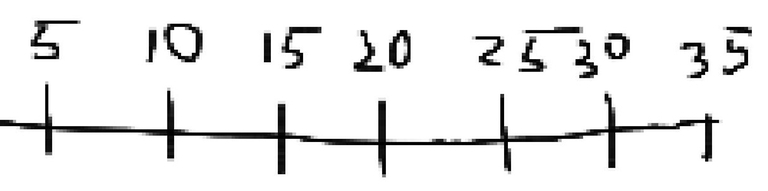 Then, here's the multiples of 7 lined up with it
Then, here's the multiples of 7 lined up with it 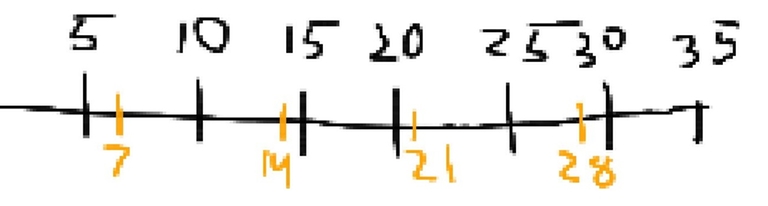 You shift the marks of 7's by 5, which represent the multiples of 7 after 5 was added to them. Then you shift them again, which represent the multiples of 7 after 2*5 was added to them. (the red are the oranges shifted by 5 once, green are shifted by 5 twice)
You shift the marks of 7's by 5, which represent the multiples of 7 after 5 was added to them. Then you shift them again, which represent the multiples of 7 after 2*5 was added to them. (the red are the oranges shifted by 5 once, green are shifted by 5 twice) 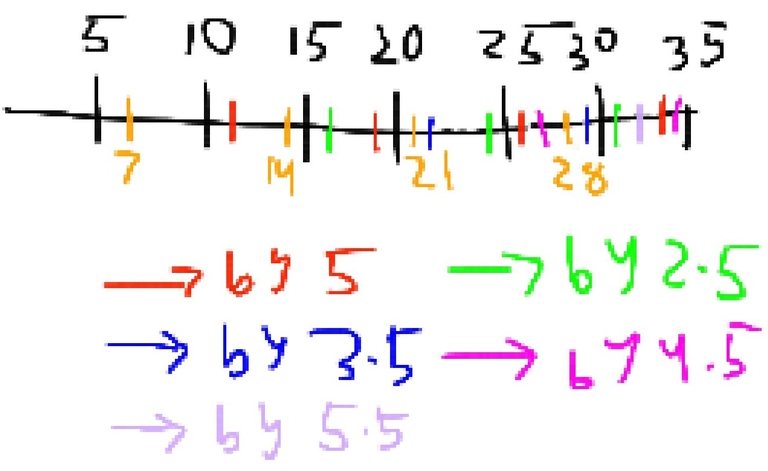 For the formula of 5*7-7-5, when you subtract 7 from 35, you get to the last orange mark, which is 28. When you subtract 5 from 28 you get the last empty mark. 28 is the last distinct mark (has a position of 3 while others have positions 1, 2, and 4) that you need to get all the numbers, as you can see from the picture. If you ignore the colors you see the positions between the multiples of 5 slowly fill up.
For the formula of 5*7-7-5, when you subtract 7 from 35, you get to the last orange mark, which is 28. When you subtract 5 from 28 you get the last empty mark. 28 is the last distinct mark (has a position of 3 while others have positions 1, 2, and 4) that you need to get all the numbers, as you can see from the picture. If you ignore the colors you see the positions between the multiples of 5 slowly fill up.
Can anybody explain what is wrong in my solution for problem C2? First step I choose all positive number and calculate the sum of them. Second step I use priority_queue to find the minimum negative number, considering the sum and the sum of prefix of positives . Third I use BIT to substract the negative number I choose Here is my code:
Your text to link here...
Can anyone share DP solution for problem 3?
see submissions of different peoples'. u might find one. ;)
You can see my submission it's pretty messy though since it's a recursive code.
Hey weakestOsuPlayer_244, I saw your code for C1 and C2 non are recursive DP. Can you please provide me the recursive DP code or maybe point out, what I'm doing wrong in my submission : 117812458 Thanks.
https://mirror.codeforces.com/contest/1526/submission/117724267
It's the same as the iterative version at least in my code I just reversed the string and updating dp recursively..
you can view this submission too.
https://mirror.codeforces.com/contest/1526/submission/117686218
Code Golf for Question B 117721466
why tag dp for problem B ? is there a dp soln too?
Here is a dp solution for method2 117718666
//PROBLEM C EASY VERSION
//GOT TLE USING MAP **** //USE MAP BECAUSE I WANT TO STORE ARRAY ELEMENTS WHICH IS NOT POSSIBLE IN 2D DP
map<pair<int, int>, int> dp;
//USE MAP PAIR FOR INDEX AND SUM OF ELEMENTS OF ARRAY
// AND STORE THE COUNT OF POTIONS
int helper(int arr[], int i, int sum,int cnt,int n){
} void solve(){ int n; cin >> n;
} signed main(){
}
//PLEASE HELP TO OPTIMIZE THIS CODE USING TOP DOWN DP **** //THEN I TRY THIS SOLUTION BY BUT THIS GIVES WRONG ANSWER **** // I DON'T KNOW HOW TO STORE LARGE VALUES IN 2D DP ****
int dp[2001][2001];
int helper(int arr[], int i, int sum,int cnt,int n){
} void solve(){
} signed main(){
}
Can AnyOne Help me with this TLE.??
Seems like you can use a vector, instead of using a map. So something like —
vector<vector<long long>> cache(n+1, vector<int>(n+1, -1)).after reading each problem in this round i felt like "no one come up with this problem before, really?", especially for problem E
it's not a good or bad, it's just a fact :)
yea the way i usually set problems is taking existing problems and twisting them.
B: I looked at 1517A - Sum of 2050 and wondered what happens if instead of $$$2050, 20500,\ldots$$$ we have $$$2050,20502050,\ldots$$$ instead.
D: The problem of minimal number of swaps is well known, so I wondered can be find a string that maximizes the number of swaps.
F: I think there are probably a few interactives with queries such as $$$|p[a]-p[b]|$$$, so I tried to make it annoying with median of $$$\{|p[a]-p[b]|,|p[b]-p[c]|,|p[a]-p[c]|\}$$$. But the turns out the solution was quite interesting.
It's crazy how difficult you can make a problem become after just a tiny change. Like one of my favourite examples is AGC51_F. I think most people might know about telling the time using two sandglasses with integer times, but I think only someone amazing like rng_58 would dare to ask what happens if one of them have a irrational time.
Problem B be like: Read the name of the problem ;) Sometimes, Name also tells the intuition behind the problem. ;)
Another approach for B, as 111=11*10+1
if the below condition satisfies, its YES
11*a+1*b=n and a>=b*10;
code : https://mirror.codeforces.com/contest/1526/submission/117686801
where σ(x)={1,if x>0 −1,if x<0, or rather σ is the sign function. Can anyone explain me the meaning of these symbols used in D problem
Yea sorry about that. I did not realize cf screwed up the formatting of it.
I have updated it in the editorial.
It was meant to look like this.
But I could not get it to render like this on cf. If anyone finds out how to do, please reply
I got it. Thank you for clarification
For Problem
1526C1,Method 2 — Greedy 1—In the editorial, we have —
Shouldn't it be non-increasing order?
Can anyone tell why problemset name is changed to bugabooset?
I am confused on C problem on test case #2.There is array of numbers -3 -3 -7 -7 -1 -7 3 3 -2 -1 0 -7. Well, if you choose -1,3,3,-2,-1 and 0, it will be non-negative result, hence the maximum number you can pick is six. Why they state in solution that the answer is five, if obviously I have proved that you can pick six of them?
Read the problem carefully, it is told that healt at any instance should be non-negative, so even if heath is negative at some point and then becomes +ve later, the answer is wrong.
What is WLOG here, in the proof of D.
Without Loss of Generality: Wikipedia. It is done to reduce the number of cases in a proof, without making the proof invalid, because there is a certain kind of symmetry.
Sorry...
How are the D1 and D2 written in the editorial of problem D? I am not getting the intuition that letters should be grouped together :( Or maybe someone can explain clearly how they come up with the intuition of grouping letters together? NVM GOT IT :)
1526B - I Hate 1111 Can someone give the solution code using method 1 in the B problem?
https://mirror.codeforces.com/contest/1526/submission/117842242
I think there is a typo in Problem E's editorial. "Now, this becomes count how many arrays of $$$(n-1+2)=(n+1)$$$ non-negative elements sum to $$$k-cnt$$$." This should be "sum to $$$k-cnt-1$$$".
Therefore final answer should be $$$ C_{n+1-1}^{n+1+k-cnt-1-1}$$$ i.e. $$$C_n^{n-1+k-cnt}$$$
Why the sum is
k - cnt - 1, we wantcntelements >= 1, so the rest sum should bek-cnt? Or am I missing something?https://mirror.codeforces.com/contest/1526/submission/117842242 for b
It's tough for me to come up with the proof of the Greedy solution of C on my own, and also, I find it very difficult to understand the proof of greedy solution of C.Any help, how can I get over this? Usually, I cannot prove my solutions clearly (It usually gets unorganised, I don't know how). Any specific advice which will help me?
https://www.youtube.com/watch?v=zf9G9x9bs9c&t=2319s this may help
can someone please give a easy mathematical proof for problem d.For me the proof given is a bit difficult to understand.
Let s be the original string and t be the optimal ans string so that the number of moves to convert t into s is maximum.
So, how do we calculate the number of moves? Basically we go on moving from left to right reading each character of si one by one , find the earliest occurence of this character in the substring t[i..n-1] and then do the swap and appropriate value to our no. of moves.
Let us assume we are currently reading the character at ith pos which is x. Also let j be the next pos where x ocuurs. So we have something like .........x????????????x????????? where ? can be any valid character other than x and '.' means we have already settled that position with appropriate character. Lets also assume that now t something looks like ..........???????x???????x???????. As you can clearly see as we move x by one our ans also increase by 1 and hence it is always optimal to club all the x's to the rightmost x in our suboptimal ans string.
THANK YOU VERY MUCH NOW I UNDERSTOOD.THANKS A LOT AGAIN
Code Can anyone help me with problem D Kill Anton? Here, I have tried to calculate the number of inversions by segment tree. I have solved 1430E-String Reversal using the same segment tree method for calculating the number of inversions, and here is my submission for that. I couldn't figure out what mistake I am making here. Here is my Code for Kill Anton.
Can C1. Potions (Easy Version) be solved using Top-Down DP?
did it just now .. you can check my submission here ... 118020188
Anyone who understood C2 using DP / SegTree given in editorial ? .... , It will be great help if it can explained in simpler words...Anyone?
aaaaa I'm fukn stupid. for problem F, I didn't realize that if there was a tie for the furthest $$$x$$$, you could simply choose any one of them.
Instead, I did the following. Consider the four numbers $$$x, y, z, w$$$. Suppose $$$x$$$ and $$$y$$$ are tied for furthest, and $$$z$$$ and $$$w$$$ are tied for second-furthest. We can repeat the same queries on those numbers using $$$(b, c)$$$ and $$$(a, c)$$$ instead of $$$(a, b)$$$. Out of those, it's guaranteed that one of them won't produce a tie for the furthest number.
needed hint 1 and a full day in order to upsolve, my brain is melted now tho :)
I have O(1) general solution for problem B (div2). Please find submission at: https://mirror.codeforces.com/contest/1526/submission/118087579
I have tried to capture the logic in the image attached. Here
Please let me know if you find error in the solution. Thanks!!
No problem I think.
Hi! can someone please explain the logic of problem D, please? I'm not able to approach the problem right.
This problem is basically a "sequel" to this other one : https://mirror.codeforces.com/problemset/problem/1430/E.
In this problem, we have an extra observation to make, which is that any optimal string will always have equal characters as a consecutive substring. The proof of this is in the editorial. Having said that, you can notice that we only have 4 different characters in our initial string (big hint) and therefore the problem is reduced to trying all $$$4!$$$ permutations of the four characters and manually counting the inversions (i did this with lazy segment tree). This last part of counting inversions is basically the same idea as the problem in the link above.
My solution : https://mirror.codeforces.com/contest/1526/submission/118123584
Thank you! This helped a lot! So the time complexity would be, O(N!(NlogN)) right? Assuming we have N unique characters? (if we use mergesort to calculate number of inversions)
It's $$$O(24Nlog(N))$$$ where $$$N$$$ is the length of the input string.
what is the intuition behind problem D's solution or how did people came up their idea ?
In Problem C Method-3
I get the solution that replacing the most negative element in the priority queue with less negative yields an optimal solution. But, I don't understand what are they trying to prove later in the explanation. In short, I don't understand the proof and also I very badly want to know that as It will help me proving other things better and also I will enjoy the proof. So, please anyone explain to me the proof that is mentioned there. Your efforts will be highly appreciated.
potions easyversion....dp method...isnt it wrong?...we need the max potions possible
Excuse me, why we can say |y2-a|<=|a-1| in Proof 4, Problem F? As we have no idea how large "a" exactly is. What if "a" were too large? Thanks for anyone's help! Noted that "pa<pb<pc" was our assumption, so there's not a range for "a", in my opinion.
Good catch!
The editorial has been updated with a (hopefully) correct proof now :)
Thanks for replying! And I think ksun48's solution was nice, that he found where 3 and N-2(or N-3)was, and try query(1,y1,y2) when y1 maybe 2 or N or N-1 and y2 maybe 3 or N-1 or N-2. If we got response "1", we found 2.
My English is not so good, sorry:)
can anyone explain c2 greedy 1 solution. i couldnt understand the editorial
why sorting (in decending) not working in problem C.
Because you can't change the order of potions.
In the solution for problem E, the last step is calculating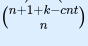
However, in the solution(python), it says k-cnt+n-1 choose n
My result is also n+k-cnt-1, and my submission is accepted https://mirror.codeforces.com/contest/1526/submission/122438057
Is there a typo, or I missed something?
Thank you!