Let's denote the sum of numbers on the upper halves of pieces as s1, and the sum on the lower halves — s2. If this sums are even, than the answer is obviously 0. Note, that if the numbers on both halves of piece have the same parity, than parity of s1 and s2 won't change after rotation this piece. If the numbers on halves have different parity, than parities of both s1 and s2 will change after rotation. Therefore, if s1 and s2 have different parities, than the answer is - 1. If both s1 and s2 are odd, than we should check, if there is a piece with numbers of different parities. If so, the answer is 1, otherwise, the answer is - 1.
Let's say for shortness, that we put numbers, that are painted on cubes, in piles, instead of cubes themselves.
Note, that the answer is the product of c1... c2, where ci is the number of different numbers in the i-th pile. Let's consider that all numbers are different. In this case the answer is n2. Now, let's suppose that we have two equal numbers and all the other are different. Then, if we put them in different piles, the answer will be n2, but if we put them in one — n·(n - 1). Obviously, the first case give greater product.
Thinking in similar manner, you can conclude, that we should do the following. Take numbers, that appear more than once, and put one of them in the first pile, one of them in the second pile and the other put aside. After that, divide the numbers, that appears once, in two equal part and put the first part in the first pile and second part in the second pile. Finally, take the numbers, that we put aside, and separate them in two pile in any kind.
Let's see on the highest bit of m. If it equals to zero, than for any 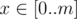 there is a zero on the (n - 1)-th position, so an - 1 doesn't affect the answer and we can put it aside and find the answer for smaller number of elements.
there is a zero on the (n - 1)-th position, so an - 1 doesn't affect the answer and we can put it aside and find the answer for smaller number of elements.
If the highest bit of m equals to 1, than an - 1 for some x will present in f(x), but for some will not. Let's consider such x, that a{n - 1} will present in f(x) with zero coefficient. It is obvious that 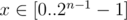 . In this case f(x) will have maximum value when x = 2n - 1 - 1. Try to update the answer by this value.
. In this case f(x) will have maximum value when x = 2n - 1 - 1. Try to update the answer by this value.
Now we should analyze the case, when 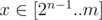 , find the maximum value of f(x) for all such x and try to update the answer by this value. Let's note, that in all such x there is 1 in (n - 1)-th position. Therefore we can find the maximum value of f(y) for all
, find the maximum value of f(x) for all such x and try to update the answer by this value. Let's note, that in all such x there is 1 in (n - 1)-th position. Therefore we can find the maximum value of f(y) for all 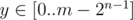 and add an - 1 to it.
and add an - 1 to it.
Note that if there are some girls in the begining of the line, they will never move. So let's remove them and will consider that the first schoolchildren in the line is a boy. Also note, the relative order of the girls doesn't change. Let's calculate for each girl such moment of time ti, that after it she won't move forever. Note, that for i-th girl ti ≥ ti - 1. Let's calculate ti in order from left to right. Let's denote yi is the position in the line where i-th girl will stop, ans xi is her current position. Therefore it is needed xi - yi second for girl to reach her finish position. So if xi - yi > ti - 1, then ti = xi - yi. Let's manage the case when xi - yi ≤ ti. The girl with number (i - 1) will be on yi-th position by ti - 1-th second, so ti ≥ ti - 1 + 1. Let's consider such moment of time p, when i-th girl stand right after (i - 1)-th, but not on yi-th position. After that, in (p + 1)-th moment of time (i - 1)-th girl and the boy standing in front of her will swap their positions, but i-th girl will save her position. Then since p + 2-th second till ti - 1 both girls will change their positions. Finally, at (ti - 1 + 1) - th second i-th girl will occupy her position. Therefore, ti = ti - 1 + 1 in this case.
Let's divide our graph on chains. Denote chain as the maximal sequence of the edges, which have the same direction. If there are more than 2 edges in each chain, then the answer is the number of such chains.
If there is a chain containing only one edge (u, v), then brute vertex, which we will take in maximal antichain (also consider the case, when we take none of them). Let's suppose we brute the vertex v. After that we put aside this vertex and all vertices, which is comparable with v. In received graph we can find the size of the maximal antichain by uning dynamic programming with O(n) time complexity. Let's show how to do this.
Write all remaining vertices in line and renumerate them from left to right by the numbers from 1 to k. After that we are going to calculate di — the size of the maximal antichain among vertices with numbers j ≥ i. So if i > k, then di = 0. In other case we can skip i-th vertex and try to update di by the value of di + 1. Also we can try to take i-th vertex to the answer. In this case we should skip all vertices, that are reachable from i-th, or the vertices, from which we can reach i-th, take the answer from the next vertex, add 1 to it and try to update the answer.











translation to English?
it will come soon)
In fact we have the strict inequality: for every ti > ti - 1
problem B can someone tell me why this code gives wrong answer ? the expected answer is so close !! http://mirror.codeforces.com/contest/353/submission/4736607
Read the comments here and you'll understand your mistake.
Good alanysis for problem D
I solve the problem E using Matching
That's too slow. There is no (not even closely) linear algorithm for matching, so you'd TLE. But in this case, the graph we're given is composed purely of a cycle of cliques connected in some vertices, on which a greedy idea works well.
But he did. Look at this nice solution.
It didn't TLE probably because of special structure of the graph.
During the contest, I did it using matching too, via Hopcroft-Karp algorithm, and some friend of mine did the same. Here are our submissions:
4735010
4735373
My question is, why this doesn't TLE? Why this graph particular structure allow that? In Wikipedia I could only find that "for random graphs it runs in near-linear time.". Are the tests weak?
I actually really like this round especially Problem D. It took me a before I could build up all the ideas to solve it. My track of thoughts is like:
1. The answer is the number of seconds needed to move the last girl to the finish place.
2. The number of seconds needed for
girl iis at least the number of seconds needed forgirl i - 1+ 1.3. The number of seconds needed for
girl iis at least the distance between the initial position and the finish position.4. Each
girl iwill move as soon as she can, so she will be right at the back of thegirl i - 1or take at mostdist(i)seconds to follow thegirl i - 1.so we can calculate the
T(i) = max(T(i-1) + 1, dist(i))and the answer is justT(lastGirl).how you computed dist[i]?
dist[i] is just the distance between the initial position and the finish position (You already know the finish position of each girl).
E can be solved by greedy, also in O(N). Let's count the lengths (as number of vertices) of individual chains (counted cyclically).
Every chain of length 3 adds 1 to the answer. That's because we could always choose a vertex from it that doesn't belong to any other chain instead of one of the side vertices that do belong to one, or instead of not choosing any vertex at all.
Now, we're left with either just a cyclic sequence of chains of length 2 (input 01010101...01 or reverse), for which the answer is the (length of the input string)/2, or some sequences of chains of length 2, each bordered by chains of length 3 on both sides. Greedy approach works here, too: no 2 chosen vertices from any such sequence can be adjacent, and we can't choose from the border. That means we can choose at most (length of such sequence-1)/2.
Was beaten hardly by problem B!! :( A great round though, I have learnt a lot!
I use a similar approach in probem D, i try to move the boys though:
for each boy, we know his initial and final position, thats the minimum time for this boy to move Actually it's the # of girls initially behind this boy
for each boy, if in the moving progress he has to stand and wait next boy to move, actually he can start in a later time so that he won's stop until arrive his final position, I call this the start time of the boy
For step 2 we can greedily precompute, and the ans is max(start time + # of girls behind) among all boys
Here's my code: 4742830
I use same basic idea, the difference is only on implementation, I didn't store that much information. here is my solution: 4735037
http://mirror.codeforces.com/contest/353/submission/4745339 this code is wa for "011001" but it is accepted.
I get wrong answer at Div2 D — Queue with this source, but I can't figure out why because of the large input. Could somebody give me a hint?