Блог пользователя abhi55

Count of rectangles that can be formed with stream of points
Автор abhi55, история, 3 года назад, По-английски

This question was asked in an online screening test. Any clue how to solve it with Online Approach better than O(N^3)?

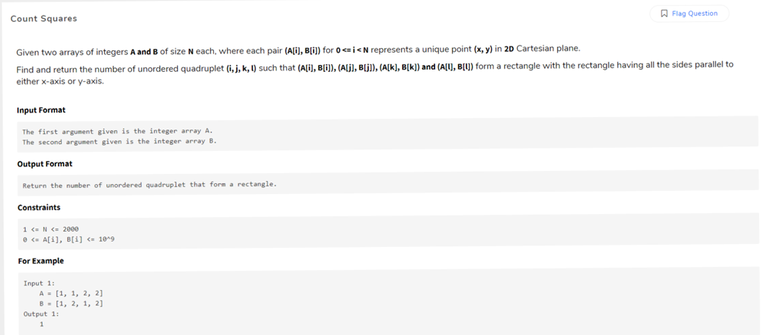
My Approach:

Maintain two maps of Map<X, Set> and Map<Y, Set> and for each point find horizontal and vertical points and for every triplet check 4th point exist or not.

  • Проголосовать: нравится
  • -4
  • Проголосовать: не нравится

»
3 года назад, # |
← Rev. 30   Проголосовать: нравится +6 Проголосовать: не нравится

Deleted

→ Ответить
  • »
    »
    3 года назад, # ^ |
      Проголосовать: нравится +4 Проголосовать: не нравится

    Why did you do this? It was the best solution out of the comments.

    It was "Iterate over the upper left and the lower right vertices, and check if the other two vertices exist."

    → Ответить
  • »
    »
    3 года назад, # ^ |
    ← Rev. 7   Проголосовать: нравится 0 Проголосовать: не нравится

    I believe that the OP's approach is also O(N^2logN). The O(N^2) comes from the cauchy schwarz inequality, and the logN from just finding the 4th point. If someone can check for its correctness.

    The structure will look like so : 

    for(every point <a,b>):
    for(every y in a): //Size ui
       for(every x in b): //Size vi
           check(x,y) exists. //O(logN)

    The total complexity except the checking part is :

    $$$\sum_{i = 0}^Nu_iv_i$$$

    Here ui and vi are the size of the lists of the current fixed <a,b> coordinate we are iterating on. N is the size of the array.

    Also we have that :

    $$$\sum_{i = 0}^{N}u_i = N$$$

    as there are total N points; same for v.

    Cauchy Schwarz states that :

    $$$\sum_{i = 0}^Nu_iv_i<= \sqrt(\sum_{i = 0}^{N}u_i^2)\times\sqrt(\sum_{i = 0}^{N}v_i^2)$$$

    The max value of

    $$$\sum_{i = 0}^{N}u_i^2$$$

    is when the list remains unpartitioned that is there is only one list of size N in which case the above sum will be

    $$$N^2$$$

    So

    $$$\sum_{i = 0}^Nu_iv_i <= \sqrt(N^2)\times\sqrt(N^2)$$$

    which is

    $$$O(N^2)$$$

    .

    → Ответить
    • »
      »
      »
      3 года назад, # ^ |
        Проголосовать: нравится 0 Проголосовать: не нравится

      The lists $$$u_i$$$ as you have defined them are not disjoint, so that it is not necessarily true that $$$\sum_{i = 0}^{N-1}u_i = N$$$. (Also, I now notice that the indices on your sums are off-by-one, fencepost-style.) In the extreme case where all x-values are the same, we have that $$$u_i = N$$$ for all $$$i$$$, so that $$$\sum_{i = 0}^{N-1}u_i = N^2$$$ and $$$\sum_{i = 0}^{N-1}u_i^2 = N^3$$$, which makes the Cauchy-Schwarz inequality yield the same $$$O(N^3)$$$ estimate as the "three nested for loops" argument.

      Nevertheless, although your argument is wrong, your conclusion is correct: The OP's approach does only check for existence of $$$O(N^2)$$$ hypothetical points. (Checking for existence of a point can be done in $$$O(1)$$$, either by using a suitably randomized hash-map or deterministically by deferring the checks to the end and using coordinate compression and a radix+bucket-sort to count the successful checks.)

      Here's a quick sketch of a correct argument: Define $$$X := \{a_i : i \in [0 .. N-1]\}$$$, and $$$P(x) := \{b_i : i \in [0 .. N-1], a_i = x\}$$$. Likewise define $$$Y$$$ and $$$Q$$$ for the array $$$b$$$. Then, the total number of hypothetical points checked can be estimated as follows:

      $$$ \displaystyle \sum_{i=0}^{N-1} |P(a_i) \times Q(b_i)| = \sum_{x \in X} \sum_{y \in P(x)} |P(x) \times Q(y)| \leq \sum_{x \in X} \sum_{y \in Y} |P(x)| \cdot |Q(y)| = N^2.$$$

      Note that this argument only works because the problem statement clarifies that each point is unique. Otherwise, we could stack all $$$N$$$ points on top of each other and the runtime would obviously be $$$\Theta(N^3)$$$ on such a test case.

      → Ответить
»
3 года назад, # |
  Проголосовать: нравится 0 Проголосовать: не нравится

Or iterate over X coords and for every pair of points (x, yi), (x, yj) add to ans how many of such pairs you meat earlier, and inc counter.

→ Ответить
»
3 года назад, # |
  Проголосовать: нравится +3 Проголосовать: не нравится
Spoiler
→ Ответить
  • »
    »
    3 года назад, # ^ |
      Проголосовать: нравится +10 Проголосовать: не нравится

    You mean it’s some ongoing contest? (Why call problem of counting rectangles “Count Squares”)

    → Ответить
»
3 года назад, # |
← Rev. 2   Проголосовать: нравится +10 Проголосовать: не нравится

I remember seeing this problem in this interview of Errichto.

There's also an elegant $$$O(n^{3/2})$$$ expected time algorithm for this problem, which combines one approach that is efficient for problem instances with few distinct x-values with another approach that is efficient for problem instances with few points associated with each x-value. Searching the web for "counting axis-aligned rectangles in O(n^3/2)" led me quickly to this page, which describes a similar algorithm and provides a source allegedly confirming this was known in 1991.

→ Ответить