The only difference between the two submissions is the cout<<"", which is there in the AC Submission and not there in WA Submission. Can someone please help me understand why printing an empty string gives a different answer than when not printing print it?
Thank you!




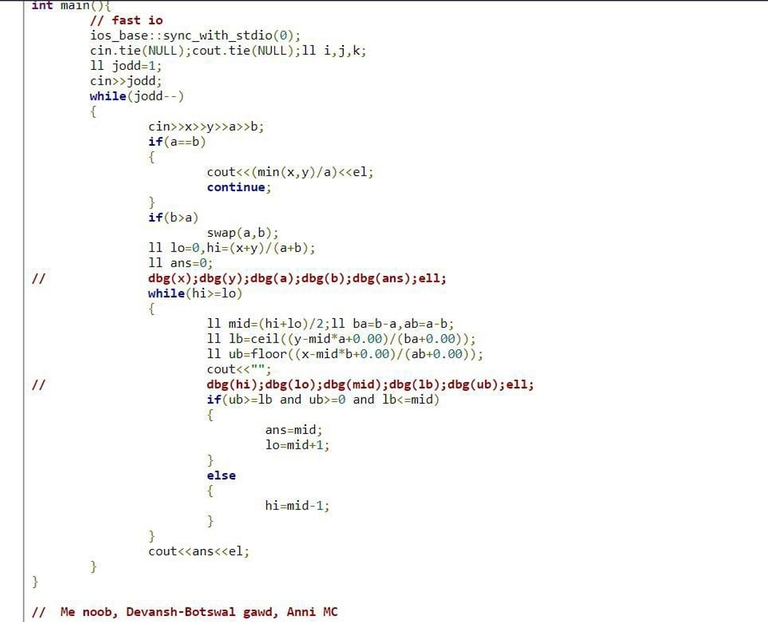








simple answer is precision errors. never use built in ceil and floor and double. Instead if you use custom built ceil and floor functions it will pass.
But how does printing the empty string affect it?
Floating point errors are weird and the results, for floating point calculations, can vary based on the system architecture, operating systems.... Check this out
Now it finally makes sense, thank you :)
Good to hear that it helped as it outweighs the downvote, I have received on the comment! LOL
People vote strangely on CF
I'd say its more looks like GCC bug
Standard not says anything about any unspecified/undefined behaviour in floating point functions. Moreover there is not any float math error as I see.
(y-mid*a+0.00)/(ba+0.00) = -1e-9and(x-mid*b+0.00)/(ab+0.00) = 1in that test case. Godbolt says that gcc produce quite different assembly code which is not seem right:Without cout
With cout
google excess precision
Could you please add a link to a good blog so I could read about it?
Thou Shalt Not Use Floating Point Numbers, gcc's bug 323 is even mentioned in their "do not report" section.
Basically, nobody implements the IEEE-754 standard for floating point numbers to the letter. If you do, you lose lots of arithmetic properties (e.g. addition is no longer associative) and optimization opportunities. Hence, compilers deviate in different ways. Another typical example is excess precision.
As a practical consequence, you should always assume that your floating point numbers are not precise. In my original post (the first link in the comment), I incorrectly assumed that $$$\varepsilon = 10^{-9}$$$ is ok when working with numbers around $$$2\cdot10^7$$$. It is not: there is not enough precision in
doublethat $$$N+\varepsilon \neq N$$$. I requested slightly more than 16 digits of precision, anddoubleis less than that.There is no excess precision: ceiling/flooring
1 / 10^9and1in double type correct. The problem is that printing empty string somehow affects order of float calculations.