Given coordinates of N points in 2D plane , you have to answer M queries in each query you are given a line (y=mx+p you are given m and p) find how many points of the N points that you are given are located under this line.
a point with coordinate (x0,y0) is located under line if (y0<m*x0+p)
N,M<=100,000
I think this problem is useful in some geometry problems so I want to know how it can be solved.
thank you.










If I didn't check the scoreboard of the current TC round, I'd have thought you're trying to get help to one problem there. I'll post the answer after the challenge phase is over.
RANT: TC is crazy random, they should have pretests of some sort. Last time I had 0 points (I solved 2 problems and forgot 2 special cases), this time I was 19. Dafuq?
BTW as you formulated it, the set of suitable points is a half-plane, therefore the answer is infinitely many. I assume you meant x- and y-coordinates in some ranges.
It's fine now. Assume the problem you described, with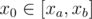 and y0 ≤ ya. That means we've got a quadrilateral with integer vertices, and count points inside. For it, we use Pick's theorem, so we need to use just GCD and vector cross product for the area of the polygon. (In TC div1 600, we needed to check if there are 3 non-collinear points in a convex polygon; if the non-collinear wasn't there, it would be just straightforward Pick.)
and y0 ≤ ya. That means we've got a quadrilateral with integer vertices, and count points inside. For it, we use Pick's theorem, so we need to use just GCD and vector cross product for the area of the polygon. (In TC div1 600, we needed to check if there are 3 non-collinear points in a convex polygon; if the non-collinear wasn't there, it would be just straightforward Pick.)
If I didn't check the scoreboard of the current TC round, I'd have thought you're trying to get help to one problem there. I'll post the answer after the challenge phase is over.
I think you are misunderstanding my problem I'm asking about a problem that is completely deferent from 600 TC problem , you should count how many points is under the line from the set of N points given to you so yes I'm asking how many points in the set of given points is in first half-plane but the answer is not infinitely many. I will edit the statement to make it clearer
BTW , I registered for TC today but I missed it :(
Oh, N given points... yeah, I misunderstood. Sorry.
Quad tree can process such query in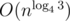 . In quad tree plane is divided by two orthogonal lines into 4 parts having approximately equal number of points. Now every line intersects at most 3 of 4 parts on each level, so we do only 3 recursive calls instead of 4. But it's still slow for such restrictions.
. In quad tree plane is divided by two orthogonal lines into 4 parts having approximately equal number of points. Now every line intersects at most 3 of 4 parts on each level, so we do only 3 recursive calls instead of 4. But it's still slow for such restrictions.
Sorry for my bad English.
Do you know if this is best known algorithm for this problem?
I don't know. This algo looks quite simple, so I doubt that it's optimal.
This seems to be an average case for quad tree, the worst will be still n2.
Once I've proposed a task to my students: given N distinct lines and N distinct points, compute for each line how many points lies on it.
All our progress was that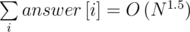
Yes, you're right. It can be O(n2) if there is more then two points on same line. But we can handle points lying on dividing lines separately, so it will be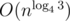 as before.
as before.
The best known upper bound is O(N4 / 3), and lower is Ω(N1 + o(1)).
Your comment may confuse somebody, because the structure you've described isn't the quad-tree in common sense. In quad-tree on each level we divide area with vertical and horisontal line in 4 equal rectangles, while in the data structure for solving this problem we divide each area with two orthogonal lines (not exactly parallel to coordinate lines) in such way that they split all points in four blocks of approximately equal size.
The great fact is that division can be done for one level with K points in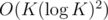 time, so the total asymptotic of building such tree is
time, so the total asymptotic of building such tree is 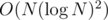 . And as NuM said in comment above, any line on the plane intersects maximum three subareas on each level, so we can process one excluded subarea in O(1), and all other subareas (each with ⌊K / 4⌋ ( + 1) points) with the recursion call. The asymptotic satisfies the equality T(N) = 3T(N / 4) + O(1), so
. And as NuM said in comment above, any line on the plane intersects maximum three subareas on each level, so we can process one excluded subarea in O(1), and all other subareas (each with ⌊K / 4⌋ ( + 1) points) with the recursion call. The asymptotic satisfies the equality T(N) = 3T(N / 4) + O(1), so 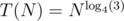 .
.
ignore
(I use ax + by + c line equation just for convenience)
Suppose all our lines have fixed a, b and different c. Then we just sort all points by ax + by and answer all queries in time using simple binary search.
time using simple binary search.
Now a, b are also variable. We can note that there are O(n2) possible different orders induced by different values of a, b (as used in the previous paragraph). Indeed, as we gradually rotate vector (a, b) (length is irrelevant) the order changes only when some two adjacent points in the current order swap their positions. Find all the critical directions of (a, b) and build the orders explicitly. Now, when we have some query ax + by + c, find the order induced by (a, b) using binary search by angle among critical angles, and then binary search again on that order. That's O(n3) preprocessing and per query. If we store the orders as persistent array (note we only need to swap two adjacent positions, so most of an array doesn't change) we achieve
per query. If we store the orders as persistent array (note we only need to swap two adjacent positions, so most of an array doesn't change) we achieve  memory and time, but
memory and time, but 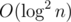 time per query. We can achieve
time per query. We can achieve  per query if we use persistent cartesian trees as persistent arrays and perform tree descent for binary search.
per query if we use persistent cartesian trees as persistent arrays and perform tree descent for binary search.
Now break initial N points into K parts of size N / K (rounding irrelevant) and perform all the procedure on each part independently. Now preprocessing takes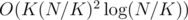 =
= 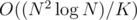 memory and time, and query takes
memory and time, and query takes 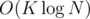 time. If we put, say,
time. If we put, say, 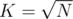 , we get
, we get 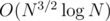 preprocessing and
preprocessing and 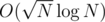 per query.
per query.
Hope I didn't miss anything.
Looks like we can combine this approach with the quad tree approach from previous comments. =)
Take K = 4Q and build quad tree of depth Q as above. Then use "leaves" of this quad tree as "parts" of our algorithm. When answering a query, we descend the quad tree until we reach leaves and then process each leave as usual. It's clear that we reach at most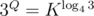 leaves, so for
leaves, so for 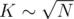 one query is processed in
one query is processed in 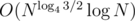 . =)
. =)
Maybe there is a better way to partite points?
Well, you made a little mistake in calcultations: 3Q is equal not to K3 / 4, but to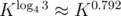 , so the total asymptotic is about
, so the total asymptotic is about 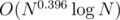 , that sounds great anyway.
, that sounds great anyway.
Thanks, fixed.
By the way, Happy Birthday! =)
Hey, thanks. =)
The total osimptotics is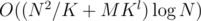 , where l = log43, so the optimal K is not
, where l = log43, so the optimal K is not  , but
, but 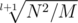 . In this way we get
. In this way we get 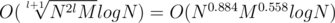 . So if N = M, we get O(N1.442logN) instead of O(N1.5logN).
. So if N = M, we get O(N1.442logN) instead of O(N1.5logN).
It seems like we can replace log43 with log64 which is slightly better. All we need is to split all the points into six sets containing almost equal number of points whith three lines which pass through common point. It can be proved that it is always possible.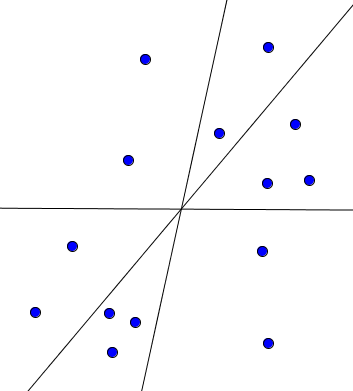
ignore
Thank you very much , I read your idea more than once I just don't understand how to get those critical angles and how to find to correct order by binary search
if you don't mind can you show me how your algorithm work for this example:
points:
lines:
thank you for your effort
Actually, critical angle corresponds to a vector that is orthogonal to some line containing some two points from the set.
That is, in your example, critical angles correspond to vectors (1, 0), (1, 1), (0, 1), (-1, 1), (-1, 0), (-1, -1), (0, -1), (1, -1) (in counter-clockwise order). Between them orders are (4, 3, 2, 1), (4, 2, 3, 1), (2, 4, 1, 3), (2, 1, 4, 3), (1, 2, 3, 4), and so on.
For a line y — 2x + c = 0 we have (a, b) = (-2, 1). It falls between critical vectors (-1, 1) and (-1, 0), so the order in mind is (2, 1, 4, 3). ax + by for all points in the same order are (-3, -1, 1, 3). So for c = 0 points 2 and 1 are separated from points 4 and 3, while for c = -2 point 3 is separated from all others.
Thank you very much , I will try to implement this idea.
It's not easy to have become numb. It only shows you have felt everything, a billion times over. And now your mind is so exhausted, it cannot even express itself anymore.