We've got n nonnegative numbers (a[i]) . We want to find the pair with maximum gcd. For example if we have:
2 4 5 15
gcd(2,4)=2
gcd(2,5)=1
gcd(2,15)=1
gcd(4,5)=1
gcd(4,15)=1
gcd(5,15)=5
The answer is 5.
n<100,000 and a[i]<100,000
I have an O(n*sqrt(n)) algorithm is there more efficient algorithm like O(n*logn) or O(n)?











Sorry for my bad English:)
This problem can be solved by brute force answer and counting how many numbers the answer divides.
It's O(R log R)
where R = maximum number in a[] array.
you have to make an array cnt[], which will keep the count of integers x.
cnt[x]=count of number x.
and code:
O(R log R), because R/1 + R/2 + ... + R/R ~ R log R
thank you very much!
I'm trying to implement this algorithm in a problem, but I'm not as good to achieve it. Can you explain a little the part of the array of count of the integers please???, with that count array, do you mean a sieve???. Thanks in advance :)
cnt[] — is not sieve.
cnt[x] — count of number x in a[]
code which calculate cnt[] :
Sorry because my english ability is not good. I think that this problem can be solved by dynamic programming. We call F[i] is the number of different elements in array a which are the mutiple of i. The result is the largest integer x that F[x] is larger than 1. We can calculate F[i] by following way. First we must initial the value of array F by F[a[i]] = F[a[i]] + 1. i = p1^m1*p2^m2*p3^m3*...*pk^mk. (k <= 7 because a[i] is smaller than 100000) If we can calculate the value of F[i] then F[i/p1] = F[i/p1] + F[i]. F[i/p2] = F[i/p2] + F[i]. F[i/p3] = F[i/p3] + F[i]. ... F[i/pk] = F[i/pk] + F[i]. You can calculate p1, p2, ..., pk in O(1). You will have more details here: http://e-maxx.ru/algo/prime_sieve_linear Because k <= 7, this approach can run in O(7*maxC) with maxC is the largest value in array a. Sorry again because my english ability is bad.
Oh, i think my algorithm has some problems.
I think this will be helpful.
Are you serious?)
ur profile picture describes my (and possibly many others') reaction after reading lovro-sinda's comment! :D
Your algorithm is so efficient you could just have used a simple cycle instead of Euclid's algorithm.
ur algorithm is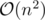 , which is much less efficient than
, which is much less efficient than 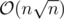 !
!
EDIT: also, the size of ur array (which, for some weird reason, is called
brojevi:P) is only1001, so ur algorithm, for large inputs, would result in RE!