Recently i was trying to solve some Project Euler question. Then i met problem #511 in which i interested a lot.
I want to share the problem and my solution with you. Here it the link to the problem.
The Problem:
let define seq(n, k) number of sequences a1...an which has this two property.
1) n is divisible by ai
2) n + a1 + a2 + ... + an is divisible by k
Two numbers n ans k are given, output seq(n, k) mod M
you may consider n < = 1012 and k < = 5000
Solution:
My solution idea came from this blog. Thanks from kien_coi_1997.
Consider dp(m, rem) which mean the answer to the problem if the the sequence size is m and sum of numbers in sequence is rem mod M.
You can recursively call function dp. consider m is odd then you can brute force a1 and find the rest with dp(m - 1, rem - ai). and if m was even you can split the sequence in to two equal sized sub-sequence. By brute forcing the sum of the first sub-sequence you can find the answer with dp(m / 2, r1) * dp(m / 2, rem - r1) .
long long dp(long long m, long long rem)
{
long long ans = 0;
if(m&1)
{
for(int i = 0; i < dv.size(); i++)
{
ans += dp(m-1, ( rem - dv[i] + k )%k );
}
}
else
{
for(int i = 0; i < k; i++)
{
ans += dp(m/2, i)*dp(m/2, (rem - i + k)%k );
}
}
return ans;
}
Then you can call function dp(n, - n) as the answer for the problem.
The time complexity of this solution is 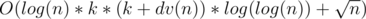
which dv(n) is number of divisors of n and log(log(n)) is because we should memoized with map
Although this solution is not very efficient but it was enough for PE, any faster solution will be appreciate.
UPD: With optimization we can reach  time complexity.
time complexity.










