This application is designed to transform test data, for example,

• 0.in|0.ans to Test01/abc.inp|Test01/abc.out,
• input/input1.txt|output/output1.txt to 01.inp|01.out,
• ... and so on.

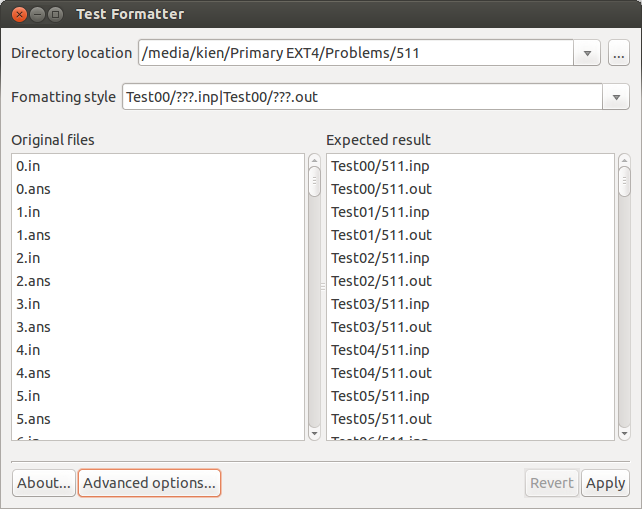
Usage

• Enter "Directory location" of a test data.
• Choose a "Formatting style" from the drop-down list (or write your own formatting style and press Enter).
• Preview the change in the box "Expected result".
• Click "Apply".

If you want to know more about "Formatting style", place cursor onto "Formatting style".

Download links

Windows

https://sites.google.com/site/kc97bla/test-formatter/testfmt3-installer.zip?attredirects=0&d=1

1. Extract testfmt3-installer.zip.
2. Run testfmt3-installer.exe as administrator (right-click, Run as administrator).
3. Follow instructions.

Linux (32-bit)

https://sites.google.com/site/kc97bla/test-formatter/testfmt3.tar.gz?attredirects=0&d=1

1. Extract testfmt3.tar.gz.
2. Run testfmt3. If you want to install it: sudo make install.

While training, contestants does not often care about pressure. So, in a contest, many people tend to adjust pressure instinctively. This auto mechanism is not good.

When you are in really high pressure, you will realize that your body becomes cold, and hands start to shake. Many people don't know why. The fact is that, in the situation, your brain are consuming very much energy, causing body's heat loss and shaky hands. Under such high pressure, you can hold on only 30-60 minutes and then become exhausted (i means run out of energy).

In this chapter, I am going to discuss about the way to master pressure (I means the way to control pressure proactively). This experience can enhance your efficiency in contests, especially helps you to prevent erratic performances.

Chapter 1. Introduction

Every activities consume energy. Usually, people tend to consume energy instinctively. However, this automatic mechanism is not really good.

I'm sure that sometimes you thought, “Today I haven't done anything”. It means in that times, you didn't consume energy effectively.

Before, I didn't control energy well too, especially in contests. I often thought that “I spent one hour doing nothing”. My worst time was in APIO 2014, I couldn't do anything in last 4 hours.

Then I realized that, it is necessary to control energy (I means consuming energy proactively). By understanding the right way to consume energy, I have got many wonderful achievements. In the team selection test in this year (a national contest which has 2 days), I got 16-17 per 20 points each days, then got rank 1 after the contest. In APIO 2015, I got 300/300 points. Although I got such scores, I didn't feel tired, but felt confortable after such contests.

I write this article in order to share my experience about controlling energy. This experience has been built for a long time, and the context in this article has been carefully checked. However, because this is personal thought, if you feel not convinced, it is usual.

.

The following code is simple, but it makes different outputs on different machine.

I knew that the reason of this strange behaviour is related to floating-point accuracy. But I can't find any considerable reasons.

#include <stdio.h>
#include <iostream>
#include <algorithm>
using namespace std;

const int N = 200005;
int n, x[N], y[N];
pair<double, double> a[N];

main() {
    scanf("%d", &n);
    for (int i=1; i<=n; i++) {
        scanf("%d%d", &x[i], &y[i]);
        a[i] = make_pair(1.0/x[i], 1.0/y[i]);
    }
    sort(a+1, a+n+1);
    
    for (int i=1; i<=n; i++)
    if (binary_search(a+1, a+n+1, make_pair(1.0/x[i], 1.0/y[i])))
    printf("%d ", i);
    cout << endl;
}

Input

3
1 3
2 2
3 1

Output on my computer (expected output)

1 2 3

Output on Codeforces

2

Can you show me the reason?

The task is classical. Given 3 points A, B, C, find a circle (I, R) that IA = IB = IC = R.

It is my solution.

• First, calculate two midpoints of AB and AC.
• Second, create two medians of AB and AC according to found midpoints.
• Finally, find the intersection of the two lines.

The above solution forces me to declare a type named 'line' and write a boring code to find the intersection of two given lines.

I think that my solution is not the best. I want to find a better one.

Any suggestions would be appreciated.

Mapping a permutation to a number has attracted much social concern. In shortest-path problems, in case a node (or state) is a permutation, we should convert states to integers, in order to BFS or Dijkstra on new graph comfortably. Many coders have known using std::map or trie to do this work. However, both have certain disadvantages. My writing will introduce a new way to solve this problem.

It is hard to write both long and detailed blog. Therefore, you can comment anything which you didn't understand well. I will reply (or update this blog if it is necessary).

To understand the role of mapping a permutation to a number, consider problem POSLOZI from COCI. Our goal is to find the length of the shortest path from a permutation S to an other permutation T using allowed operations. A valid operation is swapping two elements in the permutation. We are given a list of pair (p, q) denote we can swap the element indexed p and the element indexed q. Any other swapping operations are not allowed. A possible strategy is to BFS simultaneously from both S and T.

.

I have quite good experience in application development and I like it. Annually, I create a game and post it on Codeforces. This is my third game so I believe that many coders will like it.

Based on the approach in my previous blog, today, I found an amazing way to calculate large fibonacci numbers (in some modulo). According to part IV of my previous blog, let f(n) be the (n + 1)^th fibonacci number, we have two case: n is even and n is odd.

• f(2 * k) = f(k) * f(k) + f(k - 1) * f(k - 1)
• f(2 * k + 1) = f(k) * f(k + 1) + f(k - 1) * f(k)

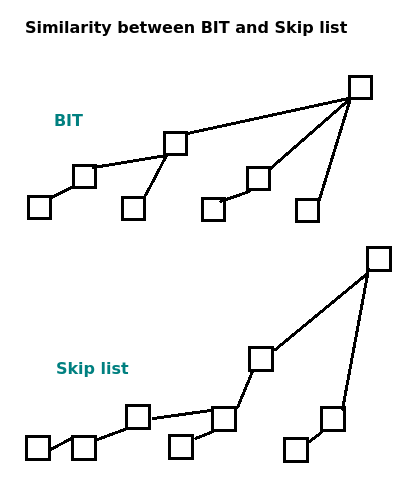
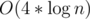There are only at most states. I don't like to prove this, but I can ensure it is true by doing some following experiment. Let's divide n into groups by depth, you will realize a special property: Each depths only contains at most 4 values of n.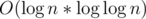

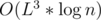call f(1000):

Depth[0] : 1000 
Depth[1] : 499 500 
Depth[2] : 248 249 250 
Depth[3] : 123 124 125 
Depth[4] : 60 61 62 63 
Depth[5] : 29 30 31 32 
Depth[6] : 13 14 15 16 
Depth[7] : 5 6 7 8 
Depth[8] : 1 2 3 4 
Depth[9] : 0 1 2 
Depth[10] : 0 1 

call f(123123123122):

Depth[0] : 123123123122 
Depth[1] : 61561561560 61561561561 
Depth[2] : 30780780779 30780780780 30780780781 
Depth[3] : 15390390388 15390390389 15390390390 15390390391 
Depth[4] : 7695195193 7695195194 7695195195 7695195196 
Depth[5] : 3847597595 3847597596 3847597597 3847597598 
Depth[6] : 1923798796 1923798797 1923798798 1923798799 
Depth[7] : 961899397 961899398 961899399 961899400 
Depth[8] : 480949697 480949698 480949699 480949700 
Depth[9] : 240474847 240474848 240474849 240474850 
Depth[10] : 120237422 120237423 120237424 120237425 
Depth[11] : 60118710 60118711 60118712 60118713 
Depth[12] : 30059354 30059355 30059356 30059357 
Depth[13] : 15029676 15029677 15029678 15029679 
Depth[14] : 7514837 7514838 7514839 7514840 
Depth[15] : 3757417 3757418 3757419 3757420 
Depth[16] : 1878707 1878708 1878709 1878710 
Depth[17] : 939352 939353 939354 939355 
Depth[18] : 469675 469676 469677 469678 
Depth[19] : 234836 234837 234838 234839 
Depth[20] : 117417 117418 117419 117420 
Depth[21] : 58707 58708 58709 58710 
Depth[22] : 29352 29353 29354 29355 
Depth[23] : 14675 14676 14677 14678 
Depth[24] : 7336 7337 7338 7339 
Depth[25] : 3667 3668 3669 3670 
Depth[26] : 1832 1833 1834 1835 
Depth[27] : 915 916 917 918 
Depth[28] : 456 457 458 459 
Depth[29] : 227 228 229 230 
Depth[30] : 112 113 114 115 
Depth[31] : 55 56 57 58 
Depth[32] : 26 27 28 29 
Depth[33] : 12 13 14 15 
Depth[34] : 5 6 7 8 
Depth[35] : 1 2 3 4 
Depth[36] : 0 1 2 
Depth[37] : 0 1 

According to the amazing property, we can calculate 10¹⁸-th fibonacci number by using little code:

#include <map>
#include <iostream>
using namespace std;

#define long long long
const long M = 1000000007; // modulo
map<long, long> F;

long f(long n) {
	if (F.count(n)) return F[n];
	long k=n/2;
	if (n%2==0) { // n=2*k
		return F[n] = (f(k)*f(k) + f(k-1)*f(k-1)) % M;
	} else { // n=2*k+1
		return F[n] = (f(k)*f(k+1) + f(k-1)*f(k)) % M;
	}
}

main(){
	long n;
	F[0]=F[1]=1;
	while (cin >> n)
	cout << (n==0 ? 0 : f(n-1)) << endl;
}

The complexity of above code is

You can reproduce my experiment by using this code.

I'm going to talking about an approach which can replace matrix multiplication in some problems. It is not only easier to implement, but also easier to adjust your code.

It is hard to write both long and detailed blog. Therefore, you can comment anything which you didn't understand well. I will reply (or update this blog if it is necessary).

I. Background

Matrix multiplication is useful. In many counting problems, when n is small, we can use DP to solve. However, when n is large (n ≈ 10⁹), we must use matrix multiplication to increase solution's speed. In solutions using matrix multiplication, generating base matrix is not easy at all. I found an good approach to solve some of those problems without matrix multiplication.

There are several advantages of my approach:

• We don't need to implement multiply operator between two matrix (A·B) and power operator (A^k).
• We don't need to spend time to generate base matrix

Besides, there are following disadvantages:

• This approach is only applicable in counting problems, it means this approach can't replace matrix multiplication in all of problems.
• I'm not sure if this approach are usable in all of counting problems (which can be solved using matrix multiplication)

II. The simplest example

For example, I will use this problem:

How many right bracket sequence which has length n and depth is not larger than L? (N ≤ 10⁹, L ≤ 10)

If n = 4 and L = 1, ()() is only right bracket sequence, but (()), (((), and ))(( is not.

Let's think about some other common ways before talking about main approach.

Firstly, because of large n, we can use matrix multiplication to use this problem. F[i] is an array of L elements, where F[i][k]=x means there are x sequence length i and current height is k. As I said above, the hardest step is to generating base matrix. Amazingly, my approach can solve this problem, and solution size is less than 30 lines.

Let's think about DP approach. It is easy to find formula f(n, h) = f(n - 1, h - 1) + f(n - 1, h + 1) that f(n, h) means number of valid sequences with n is the length of remaining sequence, h is current height. The goal is calculate f(n, 0). Of course, time complexity in this case is too large. My approach combine two approaches above.

Now, I will talk about my approach.

Let f(n, h, h0) is number of sequence length n, start at height h (current height), and end at height h0.

There are two case: n = 2 * k and n = 2 * k + 1.

• If n = 0 then return 1 if h = h0, 0 otherwise
• If n is even, we have: f(2 * k, h, h0) = sum of all f(k, h, i) * f(k, i, h0) where i in range 0..L
• If n is odd: f(2 * k + 1, h, h0) = f(2 * k, h - 1, h0) + f(2 * k, h + 1, h0)
• Additionally, we need to pay attention at following case: if h < 0 or h > L then f = 0
• The goal is output f(n, 0, 0).

The complexity of this approach is , equally to solution using matrix multiplication. Note that there are only 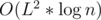states, not O(L² * n). For example, n = 100, values n in all of states will be in the set {100, 50, 25, 24, 12, 6, 3, 2, 1, 0}. Therefore, we can use index of n in above set, in other words, the depth of current state, to represent n in states instead of n.

Pseudo-code

def f(n, h, h0, Depth):
	if h<0 or h>L: return 0
	if n==0: return (h==h0 ? 1 : 0)
	if Saved[h][h0][Depth]==true: return Value[h][h0][Depth]

	if n is even:
		Result =0
		for i in 0..L: Result += f(n/2, h, i, Depth+1) * f(n/2, i, h0, Depth+1)
	else:
		Result = f(n-1, h-1, h0, Depth+1) + f(n-1, h+1, h0, Depth+1)
	
	Saved[h][h0][Depth] = true
	Value[h][h0][Depth] = Result

read n, L (from input)
output f(n, 0, 0, 0)

To explain how can Depth represent n, let n=100 for example, for each values of n, we have a value of Depth:

n 100 25 24 12 6 3 2 1 0 Depth 0 1 2 3 4 5 6 7 8

III. General case: when f(n, [a,b,c,...]) can be calculated from f(n-1, [a',b',c',...])

In this case, if you can still use matrix multiplication, you will have a big difficulty in generating base matrix. Consider following problem (I don't know where it is from):

There are t kind of flowers. In these t kinds, there are 4 kinds of flowers: gerbera, orchid, azalea and hydrangea. We use them to create a sequence with n pots of flowers. There are several conditions:

• A hydrangea must be put between an azalea and an orchid (aho or oha)
• There are at least p flower different from gerbera between any pairs of gerbera. Our goal is to find number of valid sequences.

Suppose that there are t=5 kinds of flowers: azaleas (a), hydrangeas (h), orchids (o) gerbera (g) and begonias (b) and between two gerbera, there must be at least p=3 flowers different from gerbera. With n=6, there are 2906 valid sequences, 5 of them are: aoaaoo, ahohag, gbbbgo, gbbbog, bbbbbb. Following sequences are invalid: ohoaha (substring “aha” is invalid because it should be “oha” or “aho”), gogbao (because there are not 3 flowers between g and g ), ahohah (because the last h is not adjacent with a and o ).

Constrains: n ≤ 10⁹, p ≤ 20, t ≤ 20

It is not to hard to find its DP formula: f(n, x, Just) returns number of valid sequence. Its parameters, n, x, Just, are described as follow:

• n is length of remaining sequence which we need to build.
• x is number of pots different from gerbera that I have just put them, in other words, we have just put x pots of flowers different from gerbera (you can imagine that all pots in range n+1 .. n+x are not gerbera).
• Just represents the last pot of flower (the last pot which we have just put, in other words, Just represents pot number n + 1), Just can be one of three following values, Just = 1 means azalea or orchid, Just = 2 means hydrangea, Just = 0 in other cases (included gerbera and t - 4 remaining kind of flowers)

The following code is DP function, it will work with n ≤ 10000:

long f(int n, int x, int Just) {
	if (x>=p) x=p;
	if (Just==2) {
		if (n==0) return 0;
		return f(n-1, x+1, 1);
	} else {
		if (n==0) return 1;
		if (F[x][Just].count(n)) return F[x][Just][n];
		long Sum = f(n-1, x+1, 1) * 2;
		if (Just==1) Sum += f(n-1, x+1, 2);
		if (x>=p) Sum += f(n-1, 0, 0);
		Sum += f(n-1, x+1, 0) * (t-4);
		return F[x][Just][n] = Sum % M;
	}
}
cout << f(n, ::p, 0) << endl;

Now, I will talk about correct solution. To be able to solve with n up to 10⁹, I use my above approach. Now we have f(n, p, Just, p0, Just0) means we are start from state (n, p, Just), how many way to go to state (0, p0, Just0).

To prevent misunderstanding, I will explain more about Stop parameter. Whenever Stop = true, f(n, p, Just, p0, Just, Stop) = f(n, p, Just). Whenever Stop = false, f(n, p, Just, p0, Just, Stop) = f(n, p, Just, p0, Just)$

We have two case: n = 2 * k and n = 2 * k + 1. If n = 2 * k + 1 or n = 0, we implement it as well as old DP-function. Else if n = 2 * k, f(2 * k, p, Just, p0, Just0) = sum of all f(k, p, Just, i, j) * f(k, i, j, p0, Just0) for all valid pairs of i, j (i in range 0..: : p, j in range 0..2)

Pay attention in case n = 0, n = 0 doesn't represent the end of the sequence. Because our sequence are broke into many segments, n = 0 only represents an end of a part. Therefore, I use additional parameter Stop typed boolean.

map<int, int> G[21][3][21][3][2];
#define C p][Just][p0][Just0][Stop

long g(int n, int p, int Just, int p0, int Just0, bool Stop) {	
	if (p>=::p) p=::p;
	if (n%2==1 || n==0) {
		if (Just==2) {
			if (n==0) return Stop ? 0 : p==p0 && Just==Just0;
			return g(n-1, p+1, 1, p0, Just0, Stop);
		} else {
			if (n==0) return Stop ? 1 : p==p0 && Just==Just0;
			if (G[C].count(n)) return G[C][n];
			long Sum = g(n-1, p+1, 1, p0, Just0, Stop) * 2;
			if (Just==1) Sum += g(n-1, p+1, 2, p0, Just0, Stop);
			if (p>=::p) Sum += g(n-1, 0, 0, p0, Just0, Stop);
			Sum += g(n-1, p+1, 0, p0, Just0, Stop) * (t-4);
			return G[C][n] = Sum % M;
		}
	} else {		
		if (G[C].count(n)) return G[C][n];
		long Sum = 0;
		for (int i=0; i<=::p; i++)
		for (int k=0; k<=2; k++) {
			long G1 = g(n/2, p, Just, i, k, false);
			long G2 = g(n/2, i, k, p0, Just0, Stop);
			Sum += G1*G2;
		}
		return G[C][n] = Sum % M;
	}
}

cout << g(n, ::p, 0, rand()%21, rand()%3, true) << endl;

Note that in my above code, ::p and p are different. ::p is the p in the input (how many flowers different from gerbera between any two pairs of gerbera), p is parameter of function g.

rand()%21, and rand%3 mean that those values are not important (whenever Stop==true, p0 and Just0 are not important)

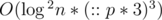The complexity of above solution is . In fact, we can avoid using map to reduce the complexity. If we do, it becomes 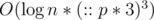, equal to the complexity of using matrix multiplication. (I used map for easier readability)

IV. f(n) = f(n-1) + f(n-2)

Now, let's calculate 10^9-th number in fibonacci sequence (in some modulo). Use matrix multiplication in this problem is easy, however, we have another way to solve this problem without using matrix multiplication. Consider following example:

You are standing at position n in Ox axis. In a step, you can move to the left 1 or 2. How many ways to reach position 0?

It is not hard to realize f(n) = f(n - 1) + f(n - 2) with f(0) = 1 and f(1) = 1. Therefore f(n) is (n+1)-th element in fibonacci sequence.

There are two cases:

• n=2*k: we have two choices: first choice is to jump from 2*k to k and jump to 0, another choice is to jump from n to k+1, move 2 step left, and jump from k-1 to 0. Therefore, f(2*k) = f(k)*f(k) + f(k-1) * f(k-1)
• n=2*k+1: consider two segments 0..k and k..n. There are two choices: first choice is to jump from n to k and jump from k to 0, another choice is to jump from n to k+1, move 2 steps to the left, and jump from k-1 to 0. Therefore, f(2*k+1) = f(k)*f(k+1) + f(k-1)*f(k).

If we stop at this point, time complexity is too large, consider case n=100:

• Depth 0: call f(100)
• Depth 1: call f(49), f(50)
• Depth 2: f(23), f(24), f(25)
• Depth 3: 10, 11, 12, 13
• …

Time complexity is now still O(n) O(log n)

We will reduce complexity as following. Let MinDepth[i] be the smallest n in Depth i, for example, array MinDepth[] in above example is {100, 49, 23, 10, …}. Now we will calculate f(25) using f(23) and f(24). Because MinDepth[2] is 23, and 25-23>=2, therefore, f(25) = f(23) + f(24).

Pseudo-code

MinDepth[] = {oo,oo,...}

def f(n, Depth):
	if n==0 or n==1: return 1
	if n-MinDepth[Depth]>=2: 
		return f(n-1, Depth) + f(n-2, Depth)

	if Saved[n]: return Value[n]
	MinDepth[Depth] = min(MinDepth[Depth], n)
	if n is even:
		Count1 = f(n/2-1, Depth+1) * f(n/2-1, Depth+1)
		Count2 = f(n/2, Depth+1) * f(n/2, Depth+1)
		Result = Count1 + Count2
	else:
		Count1 = f(n/2-1, Depth+1) * f(n/2, Depth+1)
		Count2 = f(n/2, Depth+1) * f(n/2+1, Depth+1)
		Result = Count1 + Count2
	Saved[n] = true
	Value[n] = Result

input n
output f(n,0)

• Depth 0: call f(100)
• Depth 1: call f(49), f(50)
• Depth 2: f(23), f(24), f(25)=f(23)+f(24)
• Depth 3: 10, 11, f(12)=f(10)+f(11)
• …

Time complexity now is O(logn)

V. Conclusion

It is hard to write both long and detailed blog. Therefore, you can comment anything which you didn't understand well. I will reply (or update this blog if it is necessary).

I'm going to talking about a coding style in segment tree which I used for a long time. Not only is it more systematically, but it also support more kind of segment tree.

1. Old style

Assume that we are making a segment tree support operators assign elements in a range (assign-range L R X) and get max element in a range (max-range L R).

I found a large number of people use the following way to build segment tree:

void lazy_update(int u, int ll, int rr) {
  if (Lazy[u]==-1) return; // assume that -1 is unused value
  if (ll!=rr) Lazy[u*2]=Lazy[u*2+1]=Lazy[u];
  Max[u]=Lazy[u]; Lazy[u]=-1;
}

void assign_range(int u, int ll, int rr, int L, int R, int X) {
  lazy_update(u, ll, rr); // call a function to lazy-update node u (which operate segment ll..rr)
  if (ll>R || L>rr) return;
  if (L<=ll && rr<=R) { 
    Lazy[u]=X; 
    lazy_update(u, ll, rr); 
    return; 
  }
  assign_range(2*u, ll, (ll+rr)/2, L, R, X);
  assign_range(2*u+1, (ll+rr)/2+1, rr, L, R, X);
  Max[u] = max(Max[2*u], Max[2*u+1]);
}

int max_range(int u, int ll, int rr, int L, int R) {
  lazy_update(u, ll, rr);
  if (ll>R || L>rr) return -oo;
  if (L<=ll && rr<=R) return Max[u];
  int Max1 = max_range(2*u, ll, (ll+rr)/2, L, R);
  int Max2 = max_range(2*u+1, (ll+rr)/2+1, rr, L, R);
  return max(Max1, Max2);
}

int main(){
  ...
  cin >> L >> R >> X;
  assign_range(1, 1, n, L, R, X);
  ...
  cin >> L >> R;
  cout << max_range(1, 1, n, L, R) << endl;
  ...
}

There are some duplicated code which need to be reduce:

• int u, int ll, int rr : appear in both three function declarations
• lazy_update(u, ll, rr); : appear in beginning of both two functions
• (2*u, ll, (ll+rr)/2 and 2*u+1, (ll+rr)/2+1, rr : they appear four times.

They will be reduced efficienly in new style.

2. New style

Forcing people to use a personal style is a bad idea. I share with you this style to give you a suggestion in coding segment tree.

struct node {
  int ll, rr, id;

  node(int L, int R, int X) { 
    ll=L, rr=R, id=X; 
    lazy_update(); 
  }

  node left() 
    { return node(ll, (ll+rr)/2, id*2); }
  node right() 
    { return node((ll+rr)/2+1, rr, id*2+1); }

  void lazy_update() { 
    if (Lazy[id]==-1) return; // assume that -1 is unused value
    if (ll!=rr) Lazy[id*2]=Lazy[id*2+1]=Lazy[id];
    Max[id]=Lazy[id]; Lazy[id]=-1;
  }
  
  void assign_range(int L, int R, int X){ // don't need to call lazy_update() at the beginning
    if (ll>R || L>rr) return ;
    if (L<=ll && rr<=R) 
      { Lazy[id]=X; lazy_update(); return ; }
    left().assign_range(L, R, X); // easier to read
    right().assign_range(L, R, X);
    Max[id]=max(Max[id*2], Max[id*2+1]);
  }
  
  int max_range(int L, int R) {
    if (ll>R || L>rr) return -oo;
    if (L<=ll && rr<=R) return Max[id];
    int Max1 = left().max_range(L, R);
    int Max2 = right().max_range(L, R);
    return max(Max1, Max2);
  }
};

int main(){
  ...
  cin >> L >> R >> X;
  node(1, n, 1).assign_range(L, R, X); // easier to read
  ...
  node Root(1, n, 1); // use this if we have to write to much node(1, n, 1)
  cin >> L >> R;
  cout << Root.max_range(L, R) << endl;
  ...
}

Let's list advantages of new style:

• Reduce duplicated code
• Average lines' length and functions' length is reduced.
• Easier to read

The more complex problem, the more efficient this new style.

3. Additionally feature in new style

Assume that we are facing this problem:

There is a string S which contains lowercase letters. Execute following operators on this string:

• check i j k: Check if S[i..i+k-1] is equal to S[j..j+k-1].
• delete k: Delete k-th element.

To solve above problem, we need to build a segment tree which support two operators : hash-range L R return hash value of S[L..R], and remove X remove X-th element. I called the following structure indexable segment tree. In each node, we maintain hash value and size of this node.

#define long long long

struct node {
  int ll, rr, id;
  node(int L, int X) 
    { ll=L, rr=L+Size[X]-1, id=X; }
  node left() 
    { return node(ll, id*2); }
  node right() 
    { return node(ll+Size[id*2], id*2+1); }

  void update() {
    Hash[id]=sum_hash(Hash[id*2], Hash[id*2+1], Size[id*2+1]);
    Size[id]=Size[id*2] + Size[id*2+1];
  }
  
  long hash_range(int L, int R) {
    if (ll>R || L>rr) return 0LL;
    if (L<=ll && rr<=R) return Hash[id];
    long Hash1 = left().hash_range(L, R);
    long Hash2 = right().hash_range(L, R);
    return sum_hash(Hash1, Hash2, Size[id*2+1]); // easy to implement sum_hash()
  }
  
  void remove(int X){
    if (ll>X || X>rr) return ;
    if (ll==rr) { Size[id]=0; Hash[id]=0; return; }
    right().remove(X); // if call left().remove(X) first and succeeded, ...
    left().remove(X); // ... we are not allowed to call right().remove(X)
    update();
  }

  void build(char a[], int L, int R) { // Note: ll, rr are not valid now but id
    if (L==R) 
      { Size[id]=1; Hash[id]=a[L]; return ; }
    left().build(a, L, (L+R)/2);
    right().build(a, (L+R)/2+1, R);
    update();
  }
};

char a[N]; // zero-based;

main(){
  cin >> a; n=strlen(a);
  node(0, 1).build(a, 0, n-1); // initialize segment tree
  ...
  cin >> i >> j >> k;
  long Hash1 = node(0, 1).hash_range(i, i+k-1);
  long Hash2 = node(0, 1).hash_range(j, j+k-1);
  cout << (Hash1 == Hash2 ? "Yes" : "No") << endl;
  ...
  cin >> k;
  node(0, 1).remove(k);
  ...
}

In the above code, managed segment of each nodes in segment tree is consecutively changed. And struct node become very flexible and efficient.

In this example, we are not allowed to use node Root(0, 1) because Root content is always change (rr field). If you want to use Root variable, you should update Root after every remove query: node(0, 1).remove(k); Root=node(0,1); (and I don't like this).

4. Conclusion

It is hard to write both long and detailed blog. Therefore, you can comment anything which you didn't understand well. I will reply (or update this blog if it is necessary).

I discovered a brand new approach to implement insert operator on segment tree.

1. Advantages and disadvantages

There are following advantages:

• You don't need to know what is tree rotation.
• Run extremely fast in weak tests / random test cases.

There are following disadvantages:

• Complexity of each query is O(log^2 max(n)) (amortized)
• Source code is not shorter than source using balanced tree.

This is example code for impatient people: http://paste.ubuntu.com/8148477/

Because of its complexity, I got TLE in this problem: http://www.spoj.com/problems/QMAX3VN/

Before coding this structure, I thought it will be short, but it is not. However, I want to share with you this structure because I think idea used inside this structure is nice.

2. Properties

• Size of segment tree is fixed
• In each node, we maintain two values Max and Count, if u is not leaf, Max[u]=max(Max[u*2], Max[u*2+1), Count[u]=Count[u*2]+Count[u*2+1].
• Distance between two adjacent is quite long, for example: ----100-----200-----300---- where a - means unused space.
• The longer distance between two adjacent elements were, the faster queries executed.

3. Insertion

To insert an element valued into k-th position (to be more precise operator insert(k, X) means insert X between (k-1)-th element and k-th element), we find a suitable space to put it in. If we can't find any space, re-arrange a node.

This following example will make you understand.

Firstly, segment tree is empty:

-------------

Insert 1 5: we will insert 100 into middle position:

------5------

Insert 1 6: the most suitable position is 3rd position:

--6---5------

Insert 2 7: choose middle position between element 5 and element 6:

--6-7-5------

Insert 3 8: insert 8 between 7 and 5:

--6-785------

Insert 4 9: we cannot insert 9 between 8 and 5 right now, we must rearrange a node. Let's imagine the tree:

((--6-)(785))((---)(---))

It is impossible to insert 9 between 8 and 5 because node (785) is filled, we will rearrange its parent — node ((--6-)(785)) — as follow:

• Write its elements into a line: 6, 7, 8, 5
• Insert 9 between 8 and 5: 6, 7, 8, 9, 5
• Put elements in suitable places: ------- -> -678-95, if we have more spaces, we will need to rearrange in order to distance between adjacent elements as large as possible, for example: ----------------------------- -> ----6----7----8----9----5----.

4. Accessing k-th element

• Use value Count in each node to access k-th element in O(log n)

5. Get max of range L..R

• Execute this query as other segment trees.

6. Prove the complexity

• In worst cases, each queries run in (log n)^2 amortized.
• Almost actions work in O(log n), but operator "re-arrange".

In node which have length L, we execute maximal log L operator "re-arrange", the first time occur when number of empty spaces is L/2, the second time is L/4, ...

Complexity to re-arrange a node length L is O(L).

• There is 1 node length n: O(n log n) * 1
• There is 2 nodes length n/2: O((n/2) log n) * 2 = O(n log n)
• There is 4 nodes length n/4: O((n/4) log n) * 4 = O(n log n)
• ...

In conclusion, complexity to execute n operators insert is O(n (log n)^2)

BIT does not support insert operator, but Skip list does. I realized that we can transform a Skip list into a BIT.

Example source code for impatient people:

http://paste.ubuntu.com/8119698/

My data-structure contains some operators:

• Insert x v: insert an element valued v into position x:

For instance: {10,20,30} -> insert 40 3 -> {10,20,40,30}

• Range-sum x y: return sum of elements in ranges x..y

For instance: {10,20,30} -> range-sum 2 3 -> 50

Average complexity of each operator is O(log (max n))

1. Property

a. Parent — child relationship

A is parent of B if A is the first node on the right of B and A is not shorter than B (A is higher or at least equal B height).

b. Sum and Count

In each node, we maintain a value Sum and Count.

Assume u has children u1, u2, ...

Sum[u] = Value[u] + Value[u1] + Value[u2] + ...

Count[u] = 1 + Count[u1] + Count[u2] + ...

2. Operators

a. Accessing an element x-th

• For each level (from 19 to 0), we move as far as possible but still not over x-th element (We use value Count in each node to ensure that we not go over x-th element). Additionally, we must keep array Last[] contain id of last element not exceed x-th element (to use this for later operators).

b. Insert an element into position x

• Access (x-1)-th element, Last[] let us know edges between (x-1)-th and x-th element.
• Disconnect short edges (edges which height <= new element's height), maintain Sum and Count of other elements.
• Insert new element, connect some necessary elements in Last[] with the new element, maintain Sum and Count of relevant elements.
• Connect new element with its parent, maintain Sum and Count of relevant elements.

c. Get sum of a range

Realize (Range-sum x y) = (Range-sum 1 y) — (Range-sum 1 x-1), therefore we only need to process (range-sum 1 x).

• Access x-th element
• Get sum of all of elements in Last[], if an element twice or more, we only plus once.

For example, Last[]={0,0,0,2,3,3,3} -> Answer = Sum[0] + Sum[2] + Sum[3]

3. Example source code

http://paste.ubuntu.com/8119698/

• I tested it and it worked correctly.
• It run fast, complexity of each query is about 2.5 * log (max n)

There is n integer elements. Choose k elements then calculate their GCD, call result X.

What is maximal value of X?

k<=n<=3000, k<=100, elements in range 1..10^10.

Example:

3 2
120
36
100

Sample output

20

There is a integer sequence a[1]..a[n] (some of them could be negative). We have to do m following queries:

Choose a consecutive sub-sequence a[L..R], with two positive number x and y, perform following operators: increase a[L] by x, increase a[L+1] by x+y, increase a[L+2] by x+2*y, ... increase a[R] by x+(R-L)*y.

Suppose that after kth-query, a[i] become non-negative, then Answer[i]=k. In other words, F[i] = how many queries have been done to make a[i] become >= 0. Additionally, if initialy, a[i]>=0 already, Answer[i]=0. If after m queries, a[i] is still negative, Answer[i]=-1.

Input contains n, a[1..n], m, and m queries, each query have 4 integer L, R, x, y.

Output array Answer[1..n]

Constraint: 1<=n,m<=100000, |a[i]|<=10^9, 1<=L<=R<=n, 1<=x<=n, 1<=y<=10^9.

Sample input

5
-2 -3 0 -5 -6
3
1 2 2 0
2 5 1 1
3 4 2 2

Sample output

1 2 0 3 -1

Note:

• a[3] is non-negative already, Answer[3]=0.

• After first query, a[] becomes {0,-1,0,-5,-6}, because a[1] becomes non-negative, Answer[1]=1.

• After second query, a[] becomes {0,1,3,-1,-1}, Answer[2]=2.

• After third query, a[] becomes {0,1,7,5,-1}, Answer[4]=3.

• a[5] is still negative, Answer[5]=-1.

In my profile page, it is +54: http://mirror.codeforces.com/profile/kien_coi_1997

In top-contributor page, it is +58: http://mirror.codeforces.com/top-contributed

I have checked my comments and posts, none of them have changed score.

What happened?

I have created this structure successfully some weeks ago, and I want to share it with you. This structure is fast, efficient, and it is only the improvement from segment tree. I have used this code to submit to two problems, one is in SPOJ, one is in CF. For simpliest example, consider the problem QMAX3VN on SPOJ. (http://www.spoj.com/problems/QMAX3VN/)

There are two operators: Insert X before Y-th element, and find Max between X-th element and Y-th element (inclusively).

Firstly, I use a variant of segment tree, allow us to insert element and access elements by indexes. Each node will have two childs: Left[Node] and Right[Node], by default, they are 0 (NULL). To be indexable, we must maintain array Size[].

#include <stdio.h>
#include <iostream>
#include <algorithm>
using namespace std;

#define long long long
#define f1(i,n) for (int i=1; i<=n; i++)
#define f0(i,n) for (int i=0; i<n; i++)

#define N 400005
#define oo 0x3c3c3c3c
int Max[N], Size[N], Height[N], Left[N], Right[N], Peak;

void update(int id){
   int ll=Left[id], rr=Right[id];
   Max[id]=max(Max[ll], Max[rr]);
   Size[id]=Size[ll]+Size[rr];
   Height[id]=max(Height[ll], Height[rr])+1;
}

int create(int Value){
   int id = ++Peak;
   Max[id]=Value;
   Size[id]=1;
   return id;
}

struct node {
   int ll, rr, id;
   node (int L, int X) { ll=L, id=X; rr=ll+Size[id]-1; }
   node left(){ return node(ll, Left[id]); }
   node right(){ return node(ll+Size[Left[id]], Right[id]); }

   void insert(int u, int Value) {
      if (ll>u || u>rr) return ;
      if (ll==rr) {
         Left[id]=create(Value);
         Right[id]=create(Max[id]);
         update(id); return ;
      }
      left().insert(u, Value);
      right().insert(u, Value);
      update(id);
   }

   int max_range(int L, int R) {
      if (L>rr || ll>R || L>R) return -oo;
      if (L<=ll && rr<=R) return Max[id];
      int Max1 = left().max_range(L, R);
      int Max2 = right().max_range(L, R);
      return max(Max1, Max2);
   }
};

ostream& operator << (ostream& cout, node a){
   if (a.ll==a.rr) return cout << Max[a.id];
   return cout << "(" << a.left() << " " << a.right() << ")";
   //return cout << a.left() << " " << a.right();
}

main(){
   create(-oo);
   int m; scanf("%d", &m);
   while (m--){
      char c; int x, y;
      scanf(" %c%d%d", &c, &x, &y);

      if (c=='A') node(1, 1).insert(y, x);
      else printf("%d\n", node(1, 1).max_range(x, y));
//    cout << node(1,1) << endl;
   }
}

In average case, each operators will be O(logn), but in worst case, complexity is O(n), then we will get TLE on problem QMAX3VN. I will use tree rotations in AVL tree to balance tree. Magiccally, the addtional functions are very independent with our old code. Here is some functions we need to add, it is not different from AVL tree:

int link(int ll, int u, int rr){
   Left[u]=ll, Right[u]=rr;
   return update(u), u;
}

int right_rotate(int u){ 
   int ll = Left[u]; 
   return link(Left[ll], ll, link(Right[ll], u, Right[u]));
}

int left_rotate(int u){
   int rr = Right[u];
   return link(link(Left[u], u, Left[rr]), rr, Right[rr]);
}

int balance(int u){
   if (abs(Height[Left[u]]-Height[Right[u]])<=1) return u;
   bool x=Height[Left[u]]>Height[Right[u]];
   int v=(x?Left[u]:Right[u]);
   bool y=Height[Left[v]]>Height[Right[v]];
   if (x && y) u=right_rotate(u);
   if (!x && !y) u=left_rotate(u);
   if (x && !y) { Left[u]=v=left_rotate(v); u=right_rotate(u); }
   if (!x && y) { Right[u]=v=right_rotate(v); u=left_rotate(u); }
   return u;
}

And add only two statement into Insert operator:

   void insert(int u, int Value) {
      if (ll>u || u>rr) return ;
      if (ll==rr) {
         Left[id]=create(Value);
         Right[id]=create(Max[id]);
         update(id); return ;
      }
      left().insert(u, Value);
      right().insert(u, Value);
      Left[id]=balance(Left[id]); // this one
      Right[id]=balance(Right[id]); // and this
      update(id);
   }

This is my accepted solution in problem QMAX3VN: https://sites.google.com/site/kc97ble/container/segmenttree-cpp/segmenttree-cpp-7-avl

I have used this structure to submit successully to a problem in CF. It is problem L in http://mirror.codeforces.com/gym/100125. I implemented three operator: Insert, Remove, get OR-Sum. This is my solution http://mirror.codeforces.com/gym/100125/submission/6520803.

Hope that it would be useful.

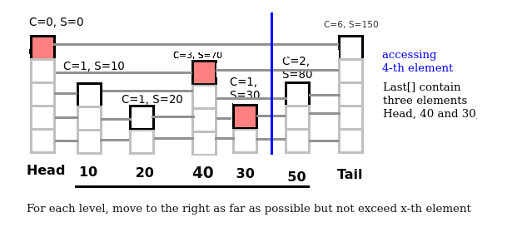
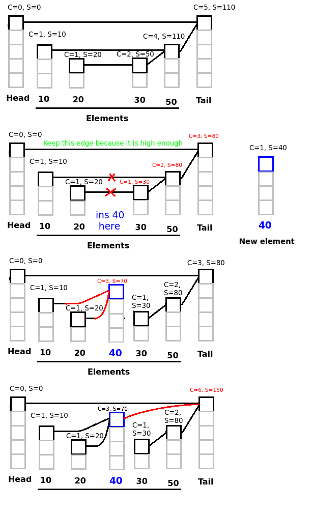
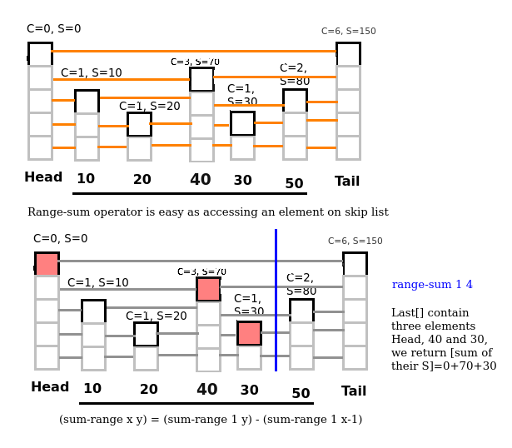
I am participating a virtual contest. I have submited a submission. But I waited too long and I don't see any response. What should we do in this problem (also in case this problem was happened in real contest)? Thank you for all of your help and replies.

Happy lunar new year. I've created a small game and hope that you would like it. (for C++ coders only and support Linux and Windows platform). Because of short time, it is not really perfect, but I think it is acceptable.

Screenshot

The letters are being pushed down. You can swap any pair of letters, to create valid C++ keywords (in a line). There are some critical letter (colored red), if it is pushed to the bottom of the table and it is not a letter of a created keyword, you lose 1 HP. There are only 10 HP, the speed is always increased.

Download

https://sites.google.com/site/kc97bla/4-game-swap/swapgame.zip?attredirects=0&d=1

Hope that everyone interested in my game.

Happy new year to everyone! I've just create a small game, and want to share it with you. This game can make you code faster. :) (for C++ coders only)

Screenshot

There are a lot of falling words. And you must type them to let them disappeared. If they pass over the bottom of screen, you will get penalty and your HP will be decreased. A correct word gains 3HP and a missed word decreases 2HP. Speed is always increased, and the game will be harder.

Download

This application supports Linux and Windows platform.

http://www.mediafire.com/download/l6fip1oohi3l89b/algorithm.zip

Hope that everyone interested in my game.

Hello everyone. I have created an application myself, then I want to share it to you :D. Of course, I don't want to let this post be an advertisement, I only want share to you an application what could be necessary with you.

Ttjudge is a free application designed to judge almost problems with test data. This can be used to judge submissions in a team, or used to train yourself. You can let submissions of your team be automatically judged after submitting like any online judges. This application has been used in my school for a year. In one year, my application has been upgraded very much. Ttjudge can recognize many testdata types. You can set time limit, checker, type of verdict (OI-like or ACM-like), and specify input/output stream.

Ttjudge supports on Linux platform only, and supports C++ submissions only, if you are using Windows, I'm sorry about this. You may want to download it here. And you may want to see Faq page and some screenshots. Thank you for your view.