First post on Codeforces. I hope you enjoy it.
Codeforces Round #215 (Div. 1) Problem C — Sereja and the Arrangement of Numbers
Analysis
Treat each q[i] as vertex, and treat each pair of a[j] and a[j+1] as an edge. What we need is a semi-Eulerian graph in which multiple edges are allowed between two edges, and each vertex must be connected to another by at least one direct edge. 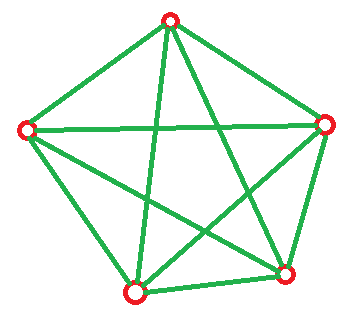
Situation for 5 vertexes, which can afford edges not less than 10.
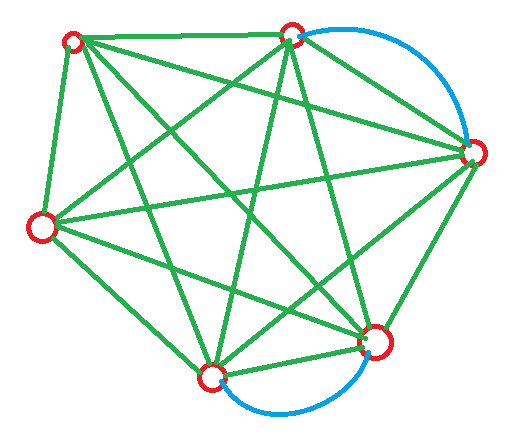
Situation for 6 vertexes, which can afford edges not less than 17.
Solve
First, calculate the maximum number of q[i]s that are available for the limit of number of edges, store it into N. Second, sort the w[] in a descending order, pick N largest costs, the sum of which is the answer.
Notice
For each given n, there are n-1 instead of n edges that are available in the graph: a[1]-a[2], a[2]-a[3], a[3]-a[4], ... , a[n-1]-a[n].
Code
#include<algorithm>
#include<cstdio>
#include<iostream>
using namespace std;
long long calc(long long limit, long long sup)
{
long long inf = 1;
while(inf < sup)
{
long long mid((inf + sup + 1) >> 1);
// for odd vertexes, the complete graph is what we need
if(mid & 1)
{
long long temp(mid * (mid - 1) >> 1);
if(temp <= limit)
inf = mid;
else
sup = mid - 1;
}
// for even vertexes, the complete graph is not semi-Eulerian
else
{
// we need to add some edges to make it semi-Eulerian
long long temp((mid * (mid - 1) >> 1) + (mid / 2 - 1));
if(temp <= limit)
inf = mid;
else
sup = mid - 1;
}
}
return inf;
}
long long value[100010];
bool cmp(long long x, long long y)
{
return y < x;
}
int main()
{
long long n, m;
scanf("%I64d%I64d", &n, &m);
n = calc(n - 1, m);
// replaces n with the result
for(long long i(0); i != m; ++i)
{
long long x;
scanf("%I64d%I64d", &x, value + i);
}
sort(value, value + m, cmp);
long long ans(0);
for(long long i(0); i != n; ++i)
ans += value[i];
printf("%I64d\n", ans);
}










