Мне показалось забавным попытаться соединить два популярных алгоритма в один

Рассмотрим следующую задачу.
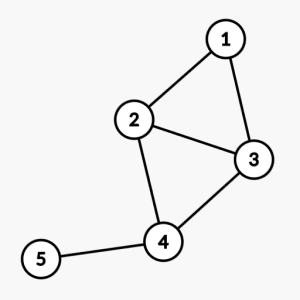
Дан связный неорграф из $$$n$$$ вершин без петель и кратных рёбер. Также задан шаблон обхода DFS — $$$a_1, a_2, \ldots, a_n$$$, который означает, что $$$i$$$-ой по счёту вершиной нужно посетить $$$a_i$$$, если $$$a_i \neq 0$$$, и любую другую иначе.
Требуется найти удовлетворяющий шаблону обход, или сообщить что такого нет.

Идея решения заключается в том, чтобы на графе всевозможных состояний обхода DFS запустить BFS.
Для одного состояния будем хранить три массива:

• used — была ли посещена вершина
• stack — текущий стек вершин
• path — общий проделанный путь

class dfs {
public:
    dfs(int n) {
        // индексация с 1
        _used.assign(n + 1, false);
        // 0 - фиктивная вершина
        _used[0] = true;
        _stack = {0};
    }

    dfs(const dfs& prev) {
        _used = prev._used;
        _stack = prev._stack;
        _path = prev._path;
    }

    // идём в новую вершину
    void push_back(int v) {
        _used[v] = true;
        _stack.push_back(v);
        _path.push_back(v);
    }

    // возвращаемся из текущей вершины
    void pop_back() {
        _stack.pop_back();
    }

    int last() {
        return _stack.back();
    }

    // изначально в стеке лежит фиктивная вершина
    bool empty() {
        return _stack.size() <= 1;
    }

    bool used(int v) {
        return _used[v];
    }

    int len() {
        return _path.size();
    }

    vector<int> path() {
        return _path;
    }

private:
    vector<bool> _used;
    vector<int> _stack, _path;
};

Заведём очередь q (как и полагается в BFS). Так как мы, скорее всего, не знаем с какой вершины нужно начать обход, создадим фиктивную вершину и соединим её со всеми остальными. Изначально в q положим состояние с этой вершиной.

Пока q не пуста, и ещё не нашли ответ, извлекаем оттуда очередное состояние cur. Пусть last — последняя вершина в стеке, то есть та вершина, в которой сейчас остановился cur. Из непосещённых соседей last выбираем те, пройдя в которые заданный порядок входов в вершины не нарушится, и добавляем нужные состояния в очередь. Если же все соседи посещены, то добавляем в очередь состояние cur, но с извлечённой из стека последней вершиной (что соответствует обратному ходу рекурсии в DFS).
Ответом будет состояние с длиной пути $$$n$$$.

Код получился несколько громоздким (большей частью из-за ООП, который был выбран для понятности), но довольно простым.

#include <iostream>
#include <vector>
#include <queue>

using namespace std;

class dfs {...};

bool check(int actual, int expected) {
    return (expected == 0 || expected == actual);
}

int main() {
    int n, m;
    cin >> n >> m;

    vector<vector<int>> graph(n + 1);
    // соединяем фиктивную вершину со всеми остальными
    for (int i = 1; i <= n; ++i) {
        graph[0].push_back(i);
    }
    for (int i = 0; i < m; ++i) {
        int v, u;
        cin >> v >> u;
        graph[v].push_back(u);
        graph[u].push_back(v);
    }
    
    // по порядковому номеру хотим получать вершину (и наоборот)
    vector<int> time2vertex(n + 1);
    vector<int> vertex2time(n + 1);
    for (int i = 0; i < n; ++i) {
        int v;
        cin >> v;
        if (v == 0) continue;
        time2vertex[i + 1] = v;
        vertex2time[v] = i + 1;
    }

    queue<dfs> q;
    q.push(dfs(n)); // кладём начальное состояние

    bool done = false;
    dfs answer(n); // здесь появится ответ
    while (!q.empty()) {
        dfs cur = q.front();
        q.pop();

        vector<int> ways; // непосещённые соседи
        for (int v : graph[cur.last()]) {
            if (!cur.used(v)) {
                ways.push_back(v);
            }
        }
        // возвращаемся в предыдущую вершину (если она есть)
        if (ways.empty() && !cur.empty()) {
            dfs next = cur;
            next.pop_back();
            q.push(next);
            continue;
        }

        for (int v : ways) {
            int time = cur.len() + 1; // следующий номер по порядку
            if (check(v, time2vertex[time]) && check(time, vertex2time[v])) { // ничего не нарушилось
                dfs next = cur;
                next.push_back(v);
                if (next.len() == n) { // нашли ответ
                    done = true;
                    answer = next;
                    break;
                }
                q.push(next);
            }
        }
        if (done) break;
    }

    if (!done) {
        cout << "No" << endl;
        return 0;
    }
    for (int e : answer.path()) {
        cout << e << ' ';
    }
}

Асимптотика
Сначала найдём $$$V, E$$$ — количество вершин и ребёр у нашего графа состояний.
Для простоты будем считать, что изначально на вход был дан полный граф и шаблон состоит полностью из нулей (то есть нет ограничений на порядок вершин). В таком случае состояние характеризуется двумя числами — длиной пройденного пути и самим путём.
При длине пути $$$0$$$ есть ровно одно состояние (состоящее из фиктивной вершины). При длине $$$= 1$$$ есть $$$n$$$ состояний и т.д. — при длине $$$i \le n$$$ есть $$$(n)_i = \frac{n!}{(n - i)!} = n \cdot (n - 1) \cdot \ldots \cdot (n - i + 1)$$$ состояний.
Тогда всего вершин $$$V = \sum_{i = 0}^n (n)_i$$$.
Из каждого состояния можно перейти в не более чем $$$n$$$ других, поэтому $$$E \le nV$$$.
BFS на графе из $$$V$$$ вершин и $$$E$$$ рёбер работает за $$$O(V + E)$$$. Также учтём, что одно состояние обрабатывается за $$$O(n)$$$ из-за копирования массивов. Итого алгоритм работает за $$$O(n^2V) = O\Big(n^2 \cdot \sum_{i = 0}^n (n)_i\Big) = O\big(n^2(n + 1)!\big)$$$.

Если учитывать ограничения на времена входа в вершины, можно получить асимптотику получше.

Warning!
Алгоритм не претендует на практическую полезность.
Любое совпадение считать случайным :)

Как известно, обычная реализация кучи не поддерживает удаление произвольного элемента по его значению. Конечно, проблема решается стандартным методом: завести хеш-таблицу и для каждого элемента кучи поддерживать указатель на его место. Не самый оптимальный по скорости написания метод. Существует другой подход, на мой взгляд, более удобный. Тем более у нас уже есть реализация кучи, и это нужно использовать.

Пусть $$$H$$$ — куча с которой мы хотим работать. Создадим новую кучу $$$Del$$$, В которую будем складывать "удаляемые элементы". То есть, когда пришёл запрос на удаление $$$x$$$, с исходной кучей ничего не происходит, мы просто берём $$$x$$$ и добавляем его в $$$Del$$$. (Для простоты я пока что считаю, что все запросы корректны, то есть удаляемый элемент гарантированно есть в $$$H$$$).

При обращении к максимальному элементу может так случиться, что он уже был удалён, поэтому надо восстановить нашу кучу. А именно, пока элементы на вершине $$$Del$$$ и $$$H$$$ совпадают — извлекаем их обоих и повторяем процедуру.

Все операции с кучами требуют $$$\mathcal{O}(\log n)$$$ времени, где $$$n$$$ — количество добавляемых/удаляемых элементов, при этом каждый из них только один раз попадает в $$$H$$$, один раз в $$$Del$$$, а также по одному разу извлекается из куч. Значит суммарное время работы $$$\mathcal{O}(n \log n)$$$.

Теперь к более важному вопросу: почему это вообще работает?

Пусть $$$m$$$ — максимальный элемент в $$$H$$$ (куча на максимум). Тогда возможны две ситуации:

1. $$$m$$$ был когда-то раньше удалён, а значит $$$m$$$ лежит в $$$Del$$$. Но так как некорректных запросов у нас пока что нет, можно утверждать, что $$$m$$$ является максимальным элементом $$$Del$$$ тоже. Алгоритм извлекает его из обеих куч и переходит к следующему максимуму.
2. $$$m$$$ не был удалён. При этом, если $$$m$$$ лежит в корне $$$H$$$, то максимум $$$Del$$$ точно меньше $$$m$$$, так как все большие уже были удалены.

Например, $$$H = [9, 6, 3, 1, 5, 2]$$$. Мы получили 3 запроса на удаление: $$$1$$$, $$$9$$$ и $$$3$$$, которые успешно положили в $$$Del$$$. То есть $$$Del = [9, 3, 1]$$$. Пытаемся извлечь элемент и ожидаем увидеть $$$6$$$ на выходе, но сейчас в корне лежит $$$9$$$ — нужно запустить процедуру восстановления кучи. Корни совпадают, а значит извлекаем их:

Теперь всё хорошо, и, как и хотели, получаем $$$6$$$. Следующий запрос извлечения не изменит вторую кучу:

Теперь опять вершины совпадают, а значит чиним кучу:

Всё отлично работает. Однако будет интереснее, если разрешить запросы, при которых элемента в куче может и не существовать. Очевидно, что текущая реализация не годится. Например, у нас была куча $$$H = [3, 2, 1]$$$ и $$$Del = []$$$. Получаем запрос на удаление $$$4$$$, и, как и полагается, кладём её в $$$Del$$$

Далее пусть идёт запрос на добавление $$$4$$$:

Теперь извлечение максимума вернёт $$$3$$$, хотя правильный ответ, конечно, $$$4$$$.

Видно, что действия по удалению должны зависеть от времени прихода элемента в кучу. Так и сделаем: вместе со значением будем хранить время добавления (в случае $$$Del$$$ — удаления) элемента из кучи. Под временем я подразумеваю количество операций, которые уже были совершены над кучей. При таком определении, например, не возникает ситуации, когда времена двух разных действий равны.

Пусть $$$m$$$ — максимальный элемент в $$$H$$$, $$$d$$$ — максимальный в $$$Del$$$ ($$$m.time$$$ и $$$d.time$$$ — времена добавления/удаления соответственно). Разберём случаи:

1. $$$m > d$$$ — Всё хорошо, возвращаем $$$m$$$.
2. $$$m < d$$$ — Очевидно, что $$$d$$$ был добавлен некорректным запросом, извлекаем его.
3. $$$m = d$$$ — Если $$$m$$$ был добавлен в $$$H$$$ раньше, чем его удалили, то есть $$$m.time < d.time$$$, то извлекаем оба. Иначе $$$m$$$ удалили раньше добавления, а такого быть не может, поэтому извлекаем только $$$d$$$.

Повторяем проверки до тех пор, пока не сможем вернуть ответ, попав в $$$1$$$ случай.

Конечно есть std::set, и он, хоть и менее эффективно, но справляется с описанной задачей, позволяя параллельно делать ещё много других вещей. Поэтому эта статья ни в коем случае не претендует на практическую полезность, а скорее описывает красивое расширение кучи, которое может быть интересно в образовательных целях.

Так что не судите строго)