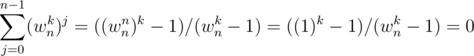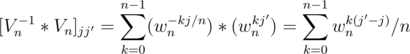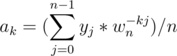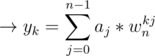Pre-requisite: Go through the Zeta/SOS DP/Yate's DP blog here
Source: This blog post is an aggregation of the explanation done by arjunarul in this video, a comment by rajat1603 here and the paper on Fast Subset Convolution
Notation:
set $$$s$$$ and mask $$$s$$$ are used interchangeably meaning the same thing.
$$$a \setminus b$$$ would mean set subtraction, i.e subtracting set $$$b$$$ from set $$$a$$$.
$$$|s|$$$ refers to the cardinality, i.e the size of the set $$$s$$$.
$$$\sum_{s' \subseteq s} f(s')$$$ refers to summing function $$$f$$$ over all possible subsets (aka submasks) $$$s'$$$ of $$$s$$$.
Aim: Given functions $$$f$$$ and $$$g$$$ both from $$$[0, 2^n)$$$ to integers. Can be represented as arrays $$$f[]$$$ and $$$g[]$$$ respectively in code. We want to compute the following transformations fast:
Zeta Transform (aka SOS DP/Yate's DP): $$$z(f(s)) = \sum_{s' \subseteq s} f(s')$$$, $$$\forall s \in [0, 2^n)$$$ in $$$O(N*2^N)$$$
Mobius Transform (i.e inclusion exclusion sum over subset): $$$\mu(f(s)) = \sum_{s' \subseteq s} (-1)^{|s \setminus s'|} f(s')$$$, $$$\forall s \in [0, 2^n)$$$ in $$$O(N*2^N)$$$. Here the term $$$(-1)^{|s \setminus s'|}$$$ just looks intimidating but simply means whether we should add the term or subtract the term in Inclusion-Exclusion Logic.
Subset Sum Convolution: $$$f \circ g(s) = \sum_{s' \subseteq s} f(s')g(s \setminus s')$$$, $$$\forall s \in [0, 2^n)$$$ in $$$O(N^2*2^N)$$$. In simpler words, take all possible ways to partition set $$$s$$$ into two disjoint partitions and sum over product of $$$f$$$ on one partition and $$$g$$$ on the complement of that partition.
Firstly, Zeta Transform is explained already here already. Just go through it first and then come back here.
Motivation: As an exercise and motivation for this blog post, you can try to come up with fast algorithms for Mobius transform and Subset Sum convolution yourself. Maybe deriving Mobius transform yourself is possible, but for Subset Sum convolution it seems highly unlikely, on the contrary if you can then you had the potential to publish the research paper mentioned in the source.
Now, let us define a relatively easy transform, i.e
Odd-Negation Transform: $$$\sigma(f(s)) = (-1)^{|s|}*f(s)$$$. This can be computed trivially in $$$O(2^{N})$$$ (assuming __builtin_popcount is $$$O(1)$$$). The name "Odd-Negation" gives the meaning of the transform, i.e if the subset $$$s$$$ is of odd cardinality then this tranform negates it, otherwise it does nothing.
Now we will show 3 important theorems (each with proof, implementation and intuition), which are as follows:
Theorem 1: $$$\sigma z \sigma(f(s)) = \mu(f(s))$$$, $$$\forall s \in [0, 2^n)$$$
Proof: For any given $$$s$$$
Now, notice two cases for parity of $$$|s|$$$
Case 1: $$$|s|$$$ is even. Then $$$(-1)^{|s|} = 1$$$.
And $$$(-1)^{|s'|} = (-1)^{|s \setminus s'|}$$$ because $$$|s'| \bmod 2 = |s \setminus s'| \bmod 2$$$, when $$$|s|$$$ is even.
So,
Case 2: $$$|s|$$$ is odd. Then $$$(-1)^{|s|} = -1$$$.
And $$$(-1)^{|s'|} = -(-1)^{|s \setminus s'|}$$$ because $$$|s'| \bmod 2 \neq |s \setminus s'| \bmod 2$$$ when $$$|s|$$$ is odd.
So,
QED.
Theorem 1 implies that mobius transform can be done by simply applying the 3 transforms one after the other like the following and it will be $$$O(N*2^N)$$$:
Implementation
// Apply odd-negation transform
for(int mask = 0; mask < (1 << N); mask++) {
if((__builtin_popcount(mask) % 2) == 1) {
f[mask] *= -1;
}
}
// Apply zeta transform
for(int i = 0; i < N; i++) {
for(int mask = 0; mask < (1 << N); mask++) {
if((mask & (1 << i)) != 0) {
f[mask] += f[mask ^ (1 << i)];
}
}
}
// Apply odd-negation transform
for(int mask = 0; mask < (1 << N); mask++) {
if((__builtin_popcount(mask) % 2) == 1) {
f[mask] *= -1;
}
}
for(int mask = 0; mask < (1 << N); mask++) mu[mask] = f[mask];
Intuition: The first $$$\sigma$$$ transform, just negates the odd masks. Then we do zeta over it, so each element stores sum of even submasks minus sum of odd submasks. Now if the $$$s$$$ being evaluated is even, then this is correct, otherwise this is inverted, since odds should be the ones being added in and evens being subtracted. Therefore, we applied the $$$\sigma$$$ transform again.
Now a somewhat, not so important theorem:
Theorem 2: $$$z^{-1}(f(s) = \mu(f(s))$$$, $$$\forall s \in [0, 2^n)$$$ i.e Inverse SOS DP/Inverse Zeta transform is equivalent to Mobius transform, i.e Zeta Transform and Mobius Transform are inversers of each other $$$z(\mu(f(s)) = f(s) = \mu(z(f(s))$$$.
The is not immediately obvious. But once someone thinks more about how to do Inverse SOS, i.e given a $$$z(f)$$$, how to obtain $$$f$$$ fast. We realise we need to do an inclusion-exclusion logic on the subsets, i.e a Mobius transform.
We will skip the proof for this, although it can be viewed from here if anyone is interested. (No Proof and Intuition section)
The interesting thing that comes out of this is that for mobius/inverse zeta/inverse SOS we have a shorter implementation which works out as follows:
Implementation
for(int i = 0; i < N; i++) {
for(int mask = 0; mask < (1 << N); mask++) {
if((mask & (1 << i)) != 0) {
f[mask] -= f[mask ^ (1 << i)]
}
}
}
for(int mask = 0; mask < (1 << N); mask++) zinv[mask] = mu[mask] = f[mask]
Here in this implementation, after the $$$i^{th}$$$ iteration, $$$f[s]$$$ will denote $$$\sum_{s' \subseteq F(i, s)} (-1)^{|s \setminus s'|} f(s')$$$, where $$$F(i, s)$$$ denotes the set of all subsets of $$$s$$$, which only differ in the lease significant $$$i$$$ bits from $$$s$$$.
That is, for a given $$$s'$$$, $$$s' \in F(i, s)$$$ IFF $$$s' \subseteq s$$$ AND ($$$s'$$$ & $$$s$$$) >> $$$i$$$ $$$=$$$ $$$s$$$ >> $$$i$$$ (i.e all bits excluding the least significant $$$i$$$ bits, match in $$$s$$$ and $$$s'$$$)
When $$$i = N$$$, we observe $$$F(N, s) = $$$ the set of all subsets of $$$s$$$ and thus we have arrived at Mobius Transform.
Another interesting observation here is that: If we generalise the statement f[mask] (+/-)= f[mask ^ (1 << i)] to f[mask] = operation(f[mask], f[mask ^ (1 << i)]), then if the operation here applied multiple times yields the same thing (Ex. Add, Max, Gcd) then it is equivalent to SOS style combine, i.e
, otherwise, it may NOT behave as SOS style combine (Ex.Subtraction)
Now the next is subset sum convolution.
Before that, let us define the following:
These just means that $$$\hat{f}(k, \dots)$$$ and $$$\hat{g}(k, \dots)$$$ will be concentrating only on those sets/masks which have cardinality size/number of bits on $$$= k$$$.
Theorem 3: $$$f \circ g(s) = z^{-1}(\sum_{i = 0}^{|s|} z(\hat{f}(i, s)) * z(\hat{g}(|s| - i, s)))$$$, $$$\forall s \in [0, 2^n)$$$
Proof:
Let $$$p(k, s)$$$ be defined as follows:
Then $$$p(|s|, s) = f \circ g(s)$$$
Proof:
Let $$$h(k, s)$$$ denote the following summation, i.e
So, the RHS of Theorem 3 looks like this:
QED.
Theorem 3 implies that subset sum convolution can be done by applying SOS and Inverse SOS DP $$$N$$$ times, for each cardinality size (Therefore complexity is $$$O(N^2*2^N)$$$), as follows:
Implementation
// Make fhat[][] = {0} and ghat[][] = {0}
for(int mask = 0; mask < (1 << N); mask++) {
fhat[__builtin_popcount(mask)][mask] = f[mask];
ghat[__builtin_popcount(mask)][mask] = g[mask];
}
// Apply zeta transform on fhat[][] and ghat[][]
for(int i = 0; i < N; i++) {
for(int j = 0; j < N; j++) {
for(int mask = 0; mask < (1 << N); mask++) {
if((mask & (1 << j)) != 0) {
fhat[i][mask] += fhat[i][mask ^ (1 << j)];
ghat[i][mask] += ghat[i][mask ^ (1 << j)];
}
}
}
}
// Do the convolution and store into h[][] = {0}
for(int mask = 0; mask < (1 << N); mask++) {
for(int i = 0; i < N; i++) {
for(int j = 0; j <= i; j++) {
h[i][mask] += fhat[j][mask] * ghat[i - j][mask];
}
}
}
// Apply inverse SOS dp on h[][]
for(int i = 0; i < N; i++) {
for(int j = 0; j < N; j++) {
for(int mask = 0; mask < (1 << N); mask++) {
if((mask & (1 << j)) != 0) {
h[i][mask] -= h[i][mask ^ (1 << j)];
}
}
}
}
for(int mask = 0; mask < (1 << N); mask++) fog[mask] = h[__builtin_popcount(mask)][mask];
Intuition: The expression
stores the sum of where $$$a$$$ is a subset of $$$s$$$, $$$b$$$ is a subset of $$$s$$$ and $$$|a| + |b| = |s|$$$. If we reframe this summation as the union of $$$a$$$ and $$$b$$$ being equal to $$$s'$$$ where $$$s'$$$ is a subset of $$$s$$$. This way, we can restate the summation as
If we see this closely, this is Inverse SOSable (can be seen because of the summation on all possible subsets of $$$s$$$). Once we do Inverse SOS, i.e apply $$$z^{-1}$$$, we get
Problems to Practice:
Problems mentioned in SOS blog, here and for Subset Sum Convolution, I only know of this as of now 914G - Sum the Fibonacci. But the technique seems super nice and I hope new problems do come up in nearby future.










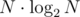 instead of the trivial
instead of the trivial 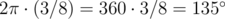 .
.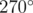 with the positive x axis in the anti clockwise direction.
with the positive x axis in the anti clockwise direction. 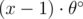 in anti clockwise direction with respect to positive x axis.
in anti clockwise direction with respect to positive x axis.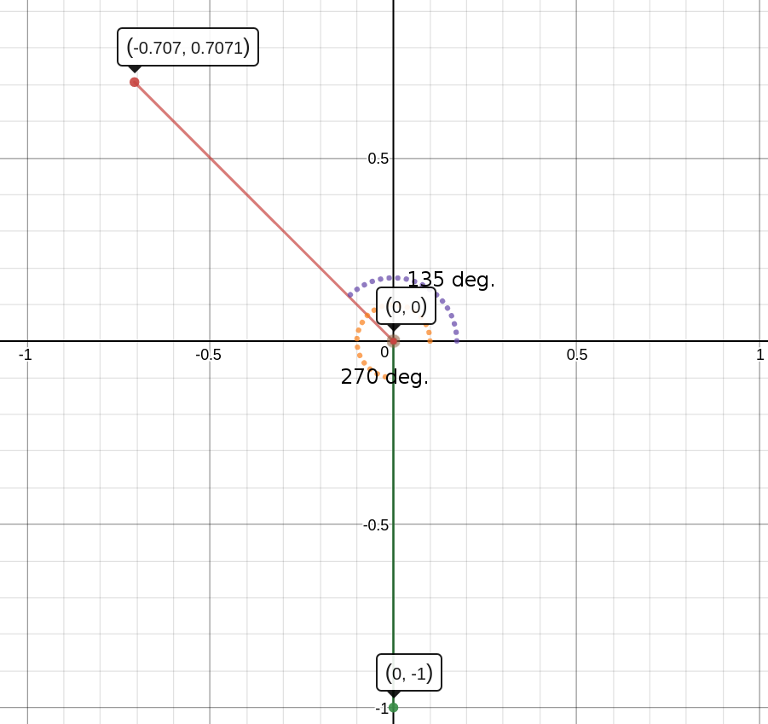
 degree with respect to positive x axis.
degree with respect to positive x axis. which are basically the points of the
which are basically the points of the 
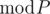 are defined as
are defined as 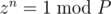 , where
, where 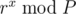 goes through all the numbers from
goes through all the numbers from 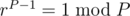 is already a fact using Fermat's Little Theorem which states that
is already a fact using Fermat's Little Theorem which states that 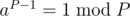 if
if 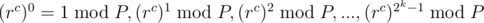
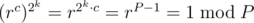
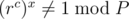 when
when 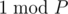 , and as
, and as 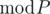 then
then 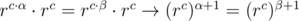 which can be generalised to
which can be generalised to 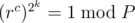 , so lets put
, so lets put 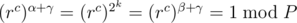 where
where 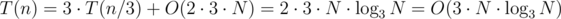
 instead of the trivial
instead of the trivial 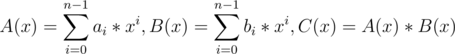
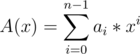 can be shown like this
can be shown like this 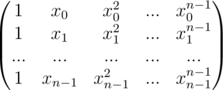
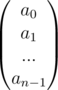
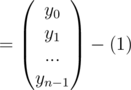
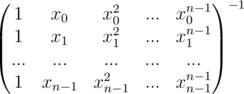
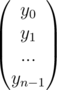
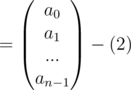
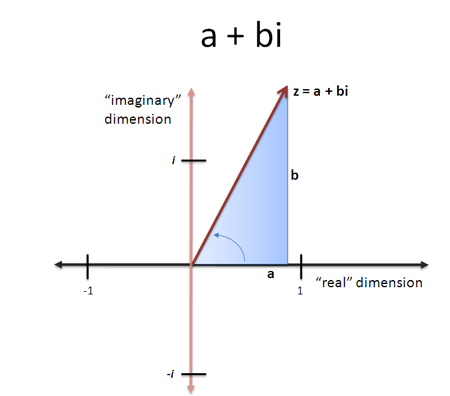
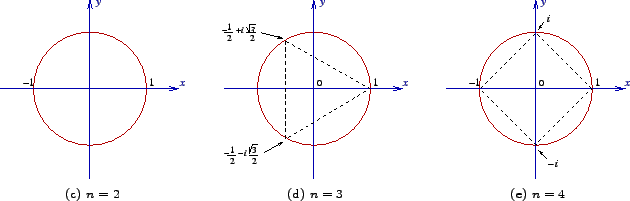
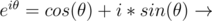 Graphically see the roots of unity in a circle then this is quite intuitive.
Graphically see the roots of unity in a circle then this is quite intuitive.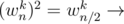 (Proved above)
(Proved above) 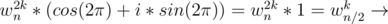 (Proved above)
(Proved above) 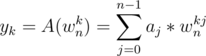
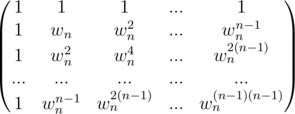

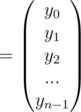
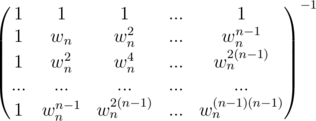

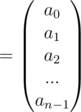
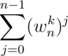
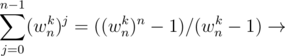 Sum of a G.P of
Sum of a G.P of