Here are the authors of the problems:
- A — Written by GlebsHP, prepared by vovuh
- B — Written by GlebsHP, prepared by vovuh
- C — zxqfl
- D — Errichto
- E — zxqfl
- F — zxqfl
- G — KAN
I'd like to thank the Codeforces team for their help, particularly KAN, who was the tester for this round.











 time, so the algorithm is
time, so the algorithm is 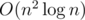 .
.
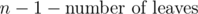 . Wait, that fails the sample case with a cycle of length 4. We have to subtract 1 if there is a vertex on the cycle with exactly 2 neighbours.
. Wait, that fails the sample case with a cycle of length 4. We have to subtract 1 if there is a vertex on the cycle with exactly 2 neighbours.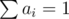

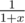 .
. 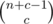 .
.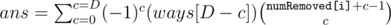
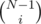 , and we have the answer. Normally you would do this with a system of linear equations, but solving a general system takes
, and we have the answer. Normally you would do this with a system of linear equations, but solving a general system takes 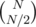 possibilities for the bracket. The complexity is
possibilities for the bracket. The complexity is 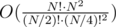 .
. weren't included. We could have
weren't included. We could have  is at the end of the window. Then, pick the the apple with the greatest index, and move it to the end of the array. You have to ensure you don't pick an apple that is immovable because of a previous value in
is at the end of the window. Then, pick the the apple with the greatest index, and move it to the end of the array. You have to ensure you don't pick an apple that is immovable because of a previous value in 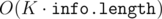 .
.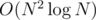 .
.
