На плоскости задан источник света. Размеры источника пренебрежимо малы, поэтому его можно считать точкой. Источник движется из точки $$$(a, s_y)$$$ в точку $$$(b, s_y)$$$ $$$(s_y < 0)$$$ по прямой со скоростью равной $$$1$$$ единица в секунду.
Также есть забор, расположенный на оси $$$OX$$$ представленный как $$$n$$$ отрезков $$$(l_i, r_i)$$$ (их настоящие координаты тогда $$$(l_i, 0)$$$ и $$$(r_i, 0)$$$). Точка $$$(x, y)$$$ является находящейся в тени, если отрезок между $$$(x,y)$$$ и текущей позицией источника света пересекается с каким-либо отрезком забора или касается его.
Вам заданы $$$q$$$ точек. Для каждой точки посчитайте суммарное время нахождения ее в тени, пока источник света движется из $$$(a, s_y)$$$ в $$$(b, s_y)$$$.
Первая строка содержит три целых числа через пробел: $$$s_y$$$, $$$a$$$ и $$$b$$$ ($$$-10^9 \le s_y < 0$$$, $$$1 \le a < b \le 10^9$$$) — соответствующие координаты источника света.
Вторая строка содержит единственное целое число $$$n$$$ ($$$1 \le n \le 2 \cdot 10^5$$$) — количество отрезков в заборе.
Следующие $$$n$$$ строк содержат по два целых числа $$$l_i$$$ и $$$r_i$$$ ($$$1 \le l_i < r_i \le 10^9$$$, $$$r_{i - 1} < l_i$$$) — отрезки в заборе заданные в возрастающем порядке. Отрезки не касаются и не пересекают друг друга.
Следующая строка содержит единственное целое число $$$q$$$ ($$$1 \le q \le 2 \cdot 10^5$$$) — количество обрабатываемых точек.
Следующие $$$q$$$ строк содержат по 2 целых числа $$$x_i$$$ и $$$y_i$$$ ($$$1 \le x_i, y_i \le 10^9$$$) — координаты точек.
Выведите $$$q$$$ строк. $$$i$$$-я строка должна содержать единственное действительное число — суммарное время нахождения в тени $$$i$$$-й точки, пока источник света движется из $$$(a, s_y)$$$ в $$$(b, s_y)$$$. Ответ будет считаться корректным, если его абсолютная или относительная погрешность не превосходит $$$10^{-6}$$$.
-3 1 6
2
2 4
6 7
5
3 1
1 3
6 1
6 4
7 6
5.000000000000000
3.000000000000000
0.000000000000000
1.500000000000000
2.000000000000000
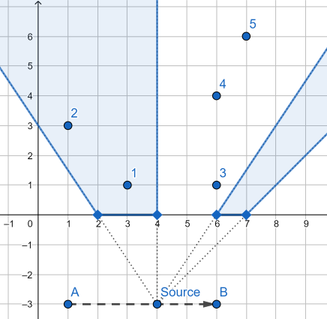
- 1-я точка все время в тени;
- 2-я точка в тени, пока источник движется от $$$(3, -3)$$$ до $$$(6, -3)$$$;
- 3-я точка в тени, когда источник находится в точке $$$(6, -3)$$$.
- 4-я точка в тени, пока источник движется от $$$(1, -3)$$$ до $$$(2.5, -3)$$$ и в точке $$$(6, -3)$$$;
- 5-я точка в тени, пока источник движется от $$$(1, -3)$$$ до $$$(2.5, -3)$$$ и от $$$(5.5, -3)$$$ до $$$(6, -3)$$$;
| Название |
|---|




