Серёже сегодня пять лет! Когда ему исполнился год, родители подарили ему число, когда ему исполнилось два годика, родители подарили ему массив целых чисел. На трёхлетие он получил строку. Когда он подрос до четырёх, его разбудила мама, тихим голосом пожелала ему быть хорошим мальчиком и дала подвешенное дерево. Сегодня он стал совсем взрослым. Он нашёл ориентированный граф без петель, подаренный ему родителями.
Так как Серёжа очень любознательный мальчик, он сразу придумал себе занятие. Он решил найти в этом графе такое множество вершин $$$Q$$$, что никакие две вершины $$$x, y \in Q$$$ не соединены ребром, а также до любой вершины $$$z \notin Q$$$ можно было дойти от какой-нибудь вершины множества $$$Q$$$ не более, чем за два шага.
Немного подумав, Сережа смог решить поставленную задачу, он ведь уже такой большой. А сможете ли вы?
Вершина $$$y$$$ достижима из вершины $$$x$$$ не более, чем за два шага, если либо существует ориентированное ребро $$$(x,y)$$$, либо существует два ориентированных ребра $$$(x,z)$$$ и $$$(z, y)$$$ для некоторой вершины $$$z$$$.
Первая строка содержит два положительных целых числа $$$n$$$ и $$$m$$$ ($$$1 \le n \le 1\,000\,000$$$, $$$1 \le m \le 1\,000\,000$$$) — количество вершин и рёбер в ориентированном графе.
Каждая из следующих $$$m$$$ строк содержит описание очередного ребра. Каждая из этих строк содержит два числа $$$a_i$$$ и $$$b_i$$$ ($$$1 \le a_i, b_i \le n$$$, $$$a_i \ne b_i$$$), задающие начало и конец $$$i$$$-го ребра. Граф может содержать кратные рёбра.
В первой строке выведите число $$$k$$$ — количество выбранных вершин. А во второй строке выведите эти $$$k$$$ чисел — номера выбранных вершин.
Если существует несколько подходящих множеств — выведите любое из них. В частности, не требуется находить множество минимального размера. Гарантируется, что хотя бы одно подходящее множество всегда существует.
5 4
1 2
2 3
2 4
2 5
4
1 3 4 5
3 3
1 2
2 3
3 1
1
3
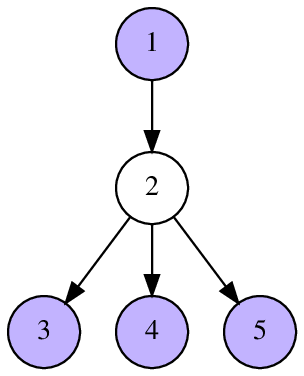
В первом примере вершины $$$1, 3, 4, 5$$$ не соединены. До вершины $$$2$$$ можно дойти за один шаг от вершины $$$1$$$.
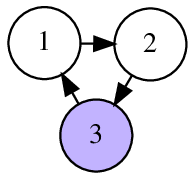
Во втором примере до вершины $$$1$$$ можно дойти за один шаг, а до вершины $$$2$$$ за два шага.
Следующие картинки иллюстрируют тесты из условия и ответы для них.
| Название |
|---|




