Существует $$$n$$$ стартапов. Стартапы могут быть либо активными либо приобретенными. Если стартап приобретенный, это означает, что его владельцем является ровно один активный стартап. Активный стартап может быть владельцем любого количества приобретенных стартапов. Активный стартап не может быть приобретенным.
Следующие действия происходят, пока существует больше одного активного стартапа. Последовательность шагов, приведенная ниже, занимает один день.
- Случайным образом равновероятно выбираются два различных активных стартапа $$$A$$$ и $$$B$$$.
- С равной вероятностью либо $$$A$$$ приобретает $$$B$$$, либо $$$B$$$ приобретает $$$A$$$ (так, если $$$A$$$ приобретает $$$B$$$, то статус $$$B$$$ меняется с активного на приобретенный, и его владельцем становится $$$A$$$).
- Когда статус стартапа меняется с активного на приобретенный, все стартапы, которыми он владел, становятся активными.
Например, может произойти следующее. Пусть $$$A$$$ и $$$B$$$ — активные стартапы, $$$C$$$, $$$D$$$, $$$E$$$ — приобретенные с владельцем $$$A$$$, а $$$F$$$, $$$G$$$ — приобретенные с владельцем $$$B$$$:

Активные стартапы показаны красным.
Если $$$A$$$ приобретет $$$B$$$, то будет следующий результат: $$$A$$$, $$$F$$$, $$$G$$$ — активные стартапы, $$$C$$$, $$$D$$$, $$$E$$$, $$$B$$$ — приобретенные с владельцем $$$A$$$, $$$F$$$ и $$$G$$$ не владеют никакими стартапами:
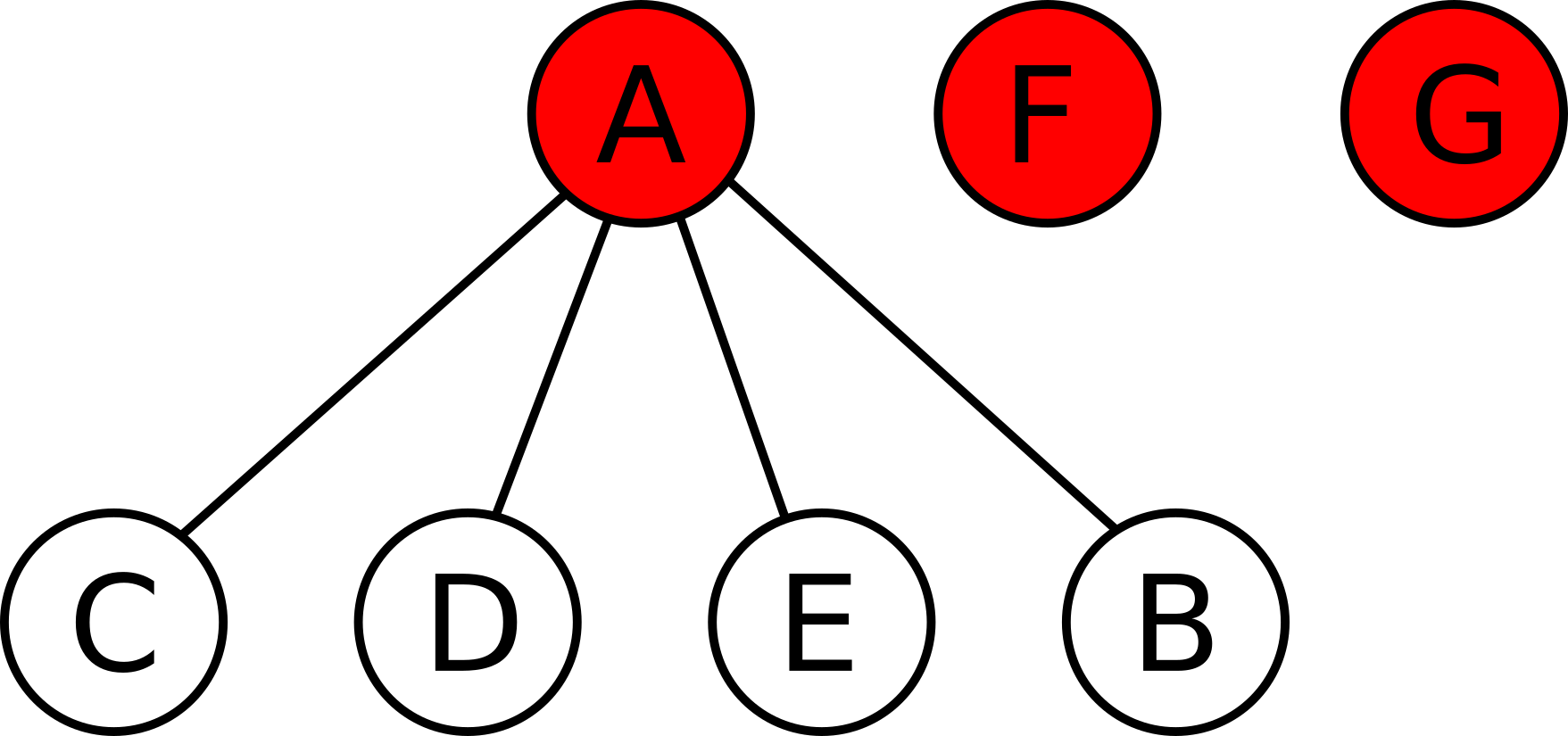
Если же $$$B$$$ приобретет $$$A$$$, то $$$B$$$, $$$C$$$, $$$D$$$, $$$E$$$ будут активными стартапами, $$$F$$$, $$$G$$$, $$$A$$$ будут приобретенными с владельцем $$$B$$$, $$$C$$$, $$$D$$$, $$$E$$$ не будут владеть никаким стартапами:
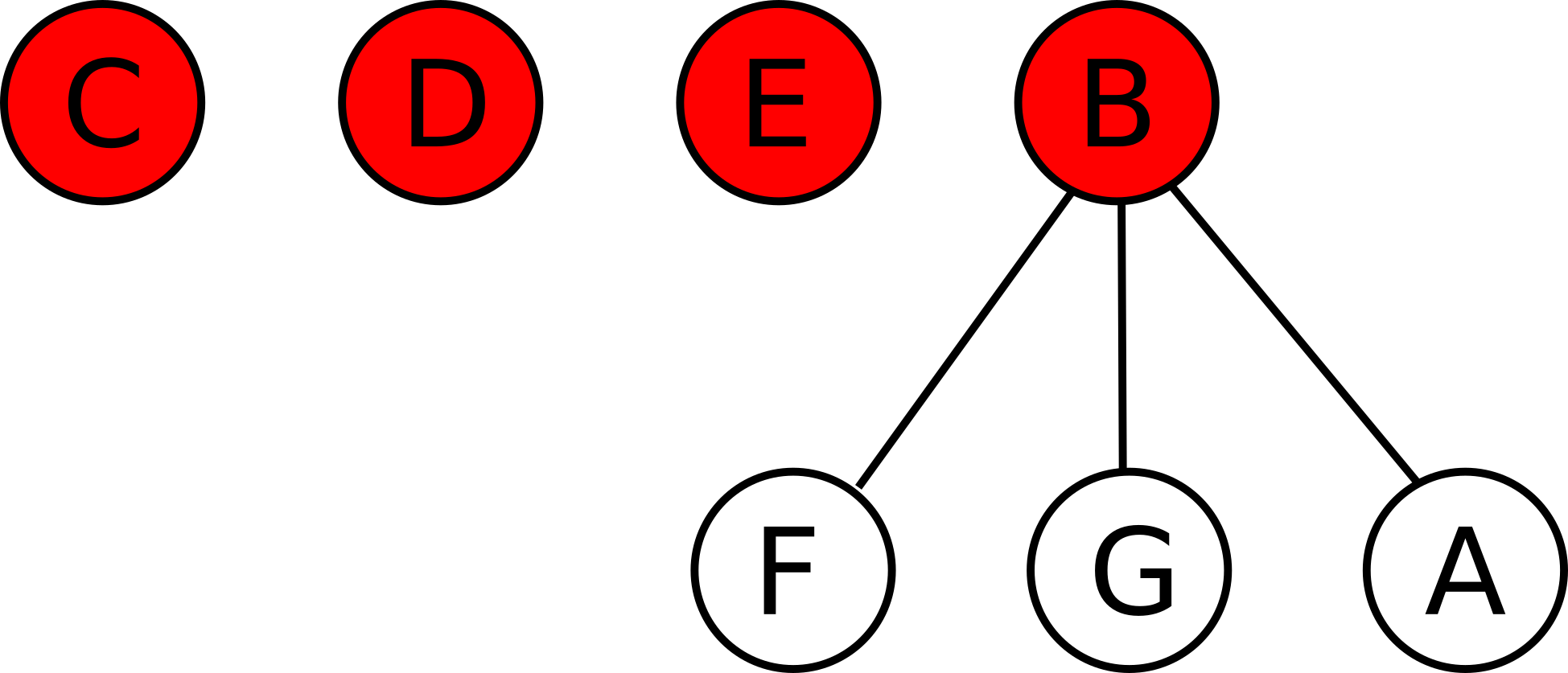
Вам даны начальные состояния стартапов. Для каждого стартапа известно, он активный или приобретенный, в последнем случае известен номер владельца.
Найдите математическое ожидание времени, необходимого для того, чтобы остался только один активный стартап и процесс завершился.
Можно показать, что математическое ожидание этого времени можно выразить как рациональное число $$$P/Q$$$, где $$$P$$$ и $$$Q$$$ — взаимно простые целые числа, и $$$Q \not= 0 \pmod{10^9+7}$$$. Выведите число $$$P \cdot Q^{-1}$$$ по модулю $$$10^9+7$$$.
Первая строка содержит одно целое число $$$n$$$ ($$$2 \leq n \leq 500$$$) — количество стартапов.
Следующая строка содержит $$$n$$$ целых чисел $$$a_1, a_2, \ldots, a_n$$$ ($$$a_i = -1$$$ или $$$1 \leq a_i \leq n$$$). Если $$$a_i = -1$$$, то это означает, что стартап $$$i$$$ является активным. В противном случае, если $$$1 \leq a_i \leq n$$$, то стартап $$$i$$$ приобретен, а его владельцем является стартап $$$a_i$$$. Гарантируется, что если $$$a_i \not= -1$$$, то $$$a_{a_i} =-1$$$ (то есть все владельцы являются активными стартапами).
Выведите единственное число — математическое ожидание времени, через которое будет существовать только один активный стартап, по модулю $$$10^9+7$$$.
3
-1 -1 -1
3
2
2 -1
0
40
3 3 -1 -1 4 4 -1 -1 -1 -1 -1 10 10 10 10 10 10 4 20 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 3 3 3 3 3 3 3 3
755808950
В первом примере есть три активных стартапа, пронумерованных $$$1$$$, $$$2$$$ и $$$3$$$, и ни одного приобретенного. Может произойти, например, следующий сценарий:
- Стартап $$$1$$$ приобретет стартап $$$2$$$ (состояние описывается массивом $$$[-1, 1, -1]$$$).
- Стартап $$$3$$$ приобретет стартап $$$1$$$ (состояние описывается массивом $$$[3, -1, -1]$$$)
- Стартап $$$2$$$ приобретет стартап $$$3$$$ (состояние описывается массивом $$$[-1, -1, 2]$$$).
- Стартап $$$2$$$ приобретет стартап $$$1$$$ (состояние описывается массивом $$$[2, -1, 2]$$$).
После этого останется только один активный стартап. Эта последовательность шагов заняла $$$4$$$ дня. Можно показать, что ожидаемое число дней равно $$$3$$$.
Во втором примере только один активный стартап, поэтому необходимо ноль дней.
В последнем примере не забудьте про модуль $$$10^9+7$$$.
| Название |
|---|




