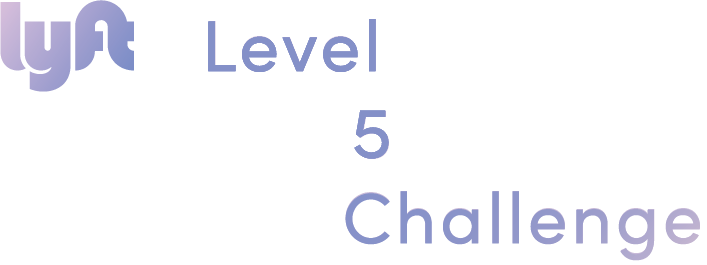Вам задана сетка $$$n \times m$$$. Каждая ячейка сетки имеет свой уникальный номер от $$$1$$$ до $$$nm$$$, то есть номера во всех ячейках разные.
За одну операцию вы можете выбрать цикл и переместить все числа на одну позицию. Здесь цикл представляет собой любую последовательность, для которой выполняются условия:
- Есть как минимум четыре ячейки.
- Каждая ячейка появляется не более одного раза.
- Каждая пара соседних ячеек, а также первая и последняя, имеют общую сторону.
Например, если бы у нас была следующая сетка:

Мы могли бы, например, выбрать такой цикл:
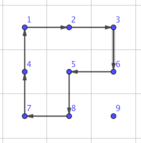
И получили бы такую сетку:
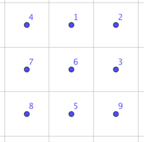
В этом конкретном случае, выбранный цикл может быть представлен как последовательность $$$[1, 2, 3, 6, 5, 8, 7, 4]$$$, в которой числа расположены в том направлении, в котором мы хотим их сместить.
Найдите любую последовательность операций, которая отсортирует сетку так, чтобы массив, созданный путем объединения строк от верхней до нижней, был отсортирован (посмотрите на первый рисунок сверху).
Обратите внимание, что вам не нужно минимизировать количество операций или сумму всех длин циклов. Единственное ограничение состоит в том, что сумма всех длин циклов не должна быть больше, чем $$$10^5$$$.
Можно показать, что в таких ограничениях ответ всегда существует. Выведите любую правильную последовательность операций, которая отсортирует сетку.
Первая строка содержит два целых числа $$$n$$$ и $$$m$$$ ($$$3 \leq n,m \leq 20$$$) — размеры сетки.
Каждая из следующих $$$n$$$ строк содержит $$$m$$$ целых чисел $$$x_{i,1}, x_{i,2}, \ldots, x_{i, m}$$$ ($$$1 \leq x_{i,j} \leq nm$$$), обозначающие значения в ячейке на пересечении строки $$$i$$$ и столбца $$$j$$$.
Гарантируется, что все $$$x_{i,j}$$$ различны.
Сначала выведите одно целое число $$$k$$$ — количество операций ($$$k \geq 0$$$).
В каждой из следующих $$$k$$$ строк выведите один цикл в формате:
$$$$$$s\ y_1\ y_2\ \ldots\ y_s$$$$$$
Где $$$s$$$ — количество ячеек в сдвиге ($$$s \geq 4$$$). Число в $$$y_1$$$ переместится в ячейку $$$y_2$$$, а число в $$$y_2$$$ переместится в ячейку $$$y_3$$$, и так далее до числа в $$$y_s$$$, которое переместится в ячейку $$$y_1$$$.
Сумма всех $$$s$$$ не должна превышать $$$10^5$$$.
3 3
4 1 2
7 6 3
8 5 9
1
8 1 4 7 8 5 6 3 2
3 5
1 2 3 5 10
11 6 4 14 9
12 7 8 13 15
3
4 4 14 13 8
4 5 10 9 4
4 12 7 6 11
Рисунки к первому примеру находятся в условии. Мы можем использовать обратную последовательность, чтобы получить первоначальную сетку.
| Название |
|---|