| Mail.Ru Cup 2018 Раунд 2 |
|---|
| Закончено |
Дан список целых чисел $$$a_1, a_2, \ldots, a_n$$$ и $$$s$$$ его подотрезков $$$[l_j; r_j]$$$ (где $$$1 \le l_j \le r_j \le n$$$).
Требуется выбрать ровно $$$m$$$ подотрезков, чтобы $$$k$$$-я порядковая статистика мультимножества чисел $$$a_i$$$, где $$$i$$$ принадлежит хотя бы одному из выбранных подотрезков, была наименьшей возможной. Если невозможно выбрать множество из $$$m$$$ подотрезков, чтобы мультимножество содержало хотя бы $$$k$$$ элементов, выведите -1.
Напомним, что $$$k$$$-й порядковой статистикой называется значение $$$k$$$-го элемента в отсортированном по возрастанию списке.
Первая строка содержит четыре целых числа $$$n$$$, $$$s$$$, $$$m$$$ и $$$k$$$ ($$$1 \le m \le s \le 1500$$$, $$$1 \le k \le n \le 1500$$$) — размер списка чисел, количество его подотрезков, количество подотрезков, которые нужно выбрать, и номер статистики.
Вторая строка содержит $$$n$$$ целых чисел $$$a_i$$$ ($$$1 \le a_i \le 10^9$$$) — значения чисел в списке.
Следующие $$$s$$$ строк содержат по два целых числа $$$l_i$$$, $$$r_i$$$ ($$$1 \le l_i \le r_i \le n$$$) — границы данных подотрезков.
Подотрезки во входных данных могут совпадать друг с другом.
Выведите одно целое число — наименьшую возможную $$$k$$$-ю порядковую статистики, или -1, если не существует ни одного способа выбрать такое множество подотрезков, чтобы мультимножество содержало хотя бы $$$k$$$ элементов.
4 3 2 2
3 1 3 2
1 2
2 3
4 4
2
5 2 1 1
1 2 3 4 5
2 4
1 5
1
5 3 3 5
5 5 2 1 1
1 2
2 3
3 4
-1
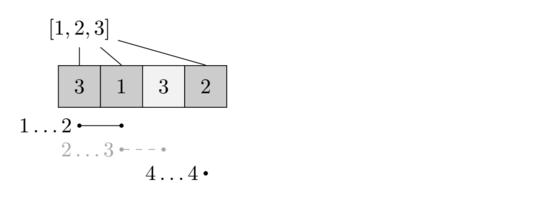
В первом примере одно из возможных решений — выбрать первый и третий подотрезок. Вместе они покрывают три элемента из исходного списка (все, кроме третьего). Тогда $$$2$$$-я порядковая статистика выбранных элементов равна $$$2$$$.
| Название |
|---|




