| Codeforces Round 520 (Div. 2) |
|---|
| Закончено |
У компании $$$X$$$ есть $$$n$$$ сотрудников, пронумерованных от $$$1$$$ до $$$n$$$. У каждого сотрудника $$$u$$$ есть его прямой начальник $$$p_u$$$ ($$$1 \le p_u \le n$$$), кроме сотрудника $$$1$$$, у которого начальника нет. Гарантируется, что значения $$$p_i$$$ образуют дерево. Сотрудник $$$u$$$ называется ответственным за сотрудника $$$v$$$, если $$$u$$$ является прямым начальником $$$v$$$ или есть такой сотрудник $$$w$$$, что $$$w$$$ ответственен за $$$v$$$, и $$$u$$$ является прямым начальником $$$w$$$. Любой сотрудник также считается ответственным за самого себя.
Также, для каждого сотрудника $$$u$$$ мы определим его уровень $$$lv(u)$$$ следующим образом:
- $$$lv(1)=0$$$
- $$$lv(u)=lv(p_u)+1$$$ если $$$u \neq 1$$$
У компании есть $$$q$$$ возможных планов на ближайшее будущее. При чём $$$i$$$-й из них задаётся двумя числа $$$l_i$$$ и $$$r_i$$$, означающими что в этом плане принимают участие все сотрудники в отрезке $$$[l_i, r_i]$$$ и только они. Чтобы всё прошло гладко, у плана должен быть проектный менеджер, который является ответственным за всех сотрудников в этом плане. Более формально, если сотрудник $$$u$$$ выбирается как проектный менеджер $$$i$$$-го плана, то для каждого сотрудника $$$v \in [l_i, r_i]$$$, $$$u$$$ должен быть ответственен за $$$v$$$. Заметим, что при этом не обязательно $$$u$$$ сам должен находится в отрезке $$$[l_i, r_i]$$$. Также, $$$u$$$ всегда выбирается таким образом, что $$$lv(u)$$$ является максимально возможным (чем больше уровень, тем меньше компания может платить сотруднику).
До того как любой план начнёт выполняться, компания позволила JATC заглянуть в свои планы. С первого взгляда он заметил, что для каждого плана можно уменьшить количество вовлечённых в него сотрудников ровно на один без каких-либо проблем. Будучи жадной, компания спрашивает у JATC: какого же именно сотрудника надо выкинуть из плана, чтобы уровень менеджера проекта был максимально возможным? JATC уже выяснил ответ и теперь предлагает это сделать и вам.
Первая строка содержит два целых числа $$$n$$$ и $$$q$$$ ($$$2 \le n \le 100\,000$$$, $$$1 \le q \le 100\,000$$$) — количество сотрудников и количество планов соответственно.
Вторая строка содержит $$$n-1$$$ целых чисел $$$p_2, p_3, \dots, p_n$$$ ($$$1 \le p_i \le n$$$), где $$$p_i$$$ является прямым начальником сотрудника $$$i$$$.
Гарантируется, что значения $$$p_i$$$ задают ориентированное дерево с корнем в вершине $$$1$$$.
Каждая из $$$q$$$ следующих строк содержит два целых числа $$$l_i$$$ и $$$r_i$$$ ($$$1 \le l_i<r_i \le n$$$) — отрезок сотрудников, вовлечённых в соответствующий план.
Выведите $$$q$$$ строк по два целых числа в каждой — номер сотрудника, которого стоит выкинуть из соответствующего плана, и максимальный уровень менеджера проекта, который в таком случае получится.
Если существует несколько способов выбрать сотрудника, которого стоит выкинуть, выведите любого из них.
11 5
1 1 3 3 3 4 2 7 7 6
4 6
4 8
1 11
9 11
8 11
4 1
8 1
1 0
11 3
8 1
В примере:
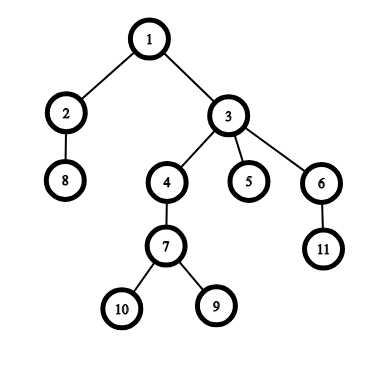
Во втором запросе, если мы выберем любого сотрудника кроме сотрудника $$$8$$$, то менеджером проекта будет сотрудник $$$1$$$, если же мы выберем сотрудника $$$8$$$, то проектным менеджером будет $$$3$$$. Так как $$$lv(3)=1 > lv(1)=0$$$, то оптимальным ответом будет выбрать сотрудника $$$8$$$.
В третьем запросе, как бы мы ни выбирали сотрудника, проектным менеджером всегда окажется сотрудник $$$1$$$.
В четвёртом запросе, если мы выберем $$$9$$$ или $$$10$$$, то менеджером проекта будет $$$3$$$, если же мы выберем $$$11$$$, то проектным менеджером окажется $$$7$$$. Так как $$$lv(7)=3>lv(3)=1$$$, то оптимальным ответом будет выбрать сотрудника $$$11$$$.
| Название |
|---|




