| Codeforces Round 520 (Div. 2) |
|---|
| Закончено |
В королевстве $$$X$$$ есть $$$n$$$ городов, пронумерованных от $$$1$$$ до $$$n$$$. Люди путешествуют между городами используя различные односторонние дороги. Как пассажир, JATC нашёл странным, что для любого города $$$u$$$ нельзя начать в нём поездку и после этого в него же и вернуться. Тем самым, королевство представляет из себя ациклический граф.
Будучи раздражённым дорожной системой, JATC решил встретиться с королём и попросить его сделать хоть что-нибудь. В ответ король сказал, что он собирается модернизировать некоторые города, чтобы улучшить транспортную ситуацию. Однако, в целях экономии бюджета, король хочет модернизировать только важные или полуважные города. Город $$$u$$$ называется важным, если для любого города $$$v \neq u$$$ есть путь или из $$$v$$$ в $$$u$$$, или из $$$u$$$ в $$$v$$$. Город $$$u$$$ называется полуважным, если он важным не является, но можно удалить ровно одну вершину $$$v \neq u$$$, так что $$$u$$$ станет важным. Король собирается перейти к действиям, сразу как только обнаружит все эти города. Помогите ему с этим, чтобы ускорить процесс.
Первая строка входных данных содержит два целых числа $$$n$$$ и $$$m$$$ ($$$2 \le n \le 300\,000$$$, $$$1 \le m \le 300\,000$$$) — количество городов и количество односторонних дорог.
Следующие $$$m$$$ строк содержат описанние дорожной системы королевства. Каждая из них содержит два целых числа $$$u_i$$$ и $$$v_i$$$ ($$$1 \le u_i, v_i \le n$$$, $$$u_i \neq v_i$$$), обозначающих одностороннюю дорогу из $$$u_i$$$ в $$$v_i$$$.
Гарантируется, что города королевства образуют ациклический граф, не содержащий кратных рёбер и петель.
Выведите одно целое число — количество городов, которые нужно модернизировать.
7 7
1 2
2 3
3 4
4 7
2 5
5 4
6 4
4
6 7
1 2
2 3
3 4
1 5
5 3
2 6
6 4
4
В первом примере:
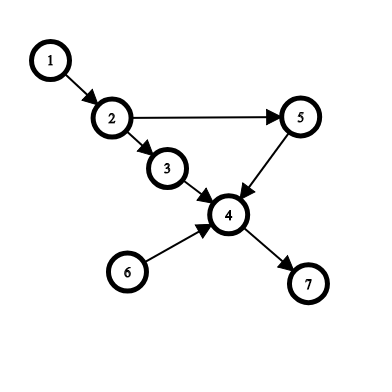
- Начиная из города $$$1$$$ мы можем добраться до всех городов, кроме города $$$6$$$. Также из города $$$6$$$ мы не можем добраться до города $$$1$$$. Тем самым, если мы удалим города $$$6$$$, город $$$1$$$ станет важным. Значит город $$$1$$$ является полуважным.
- Для города $$$2$$$ множество городов, которые не достижимы из $$$2$$$, и из которых не достижима $$$2$$$ равно $$$\{6\}$$$. Тем самым удаление города $$$6$$$ делает город $$$2$$$ важным. Значит город $$$2$$$ полуважный.
- Для города $$$3$$$ соответствующее множество равно $$$\{5, 6\}$$$. Тем самым удаление ни города $$$5$$$, ни $$$6$$$ не сделает город $$$3$$$ важным. Значит он не является важным или полуважным.
- Для города $$$4$$$ соответствующее множество пусто, следовательно город $$$4$$$ является важным.
- У города $$$5$$$ это множество равно $$$\{3, 6\}$$$, а у города $$$6$$$ равно $$$\{3, 5\}$$$. Поэтому также как и город $$$3$$$ они не являются важными или полуважными.
- Город $$$7$$$ является важным, так как в него можно добраться из любого другого города.
Во втором примере важными являются города $$$1$$$ и $$$4$$$, а города $$$2$$$ и $$$3$$$ являются полуважными.
| Название |
|---|




