| Codeforces Round 515 (Div. 3) |
|---|
| Закончено |
Максим ходит по декартовой плоскости. Он начинает в точке $$$(0, 0)$$$ и за один ход он может перейти в любую из четырех соседних точек (влево, вправо, вверх, вниз). Например, если сейчас Максим находится в точке $$$(0, 0)$$$, то за один ход он может пойти в точки:
- $$$(1, 0)$$$;
- $$$(0, 1)$$$;
- $$$(-1, 0)$$$;
- $$$(0, -1)$$$.
Также на плоскости есть $$$n$$$ различных ключевых точек. $$$i$$$-я точка равна $$$p_i = (x_i, y_i)$$$. Гарантируется, что $$$0 \le x_i$$$ и $$$0 \le y_i$$$ и нет ключевой точки $$$(0, 0)$$$.
Назовем точками первого уровня такие точки, что $$$max(x_i, y_i) = 1$$$, точками второго уровня такие точки, что $$$max(x_i, y_i) = 2$$$ и так далее. Максим хочет посетить все ключевые точки. Но он не хочет посещать точки уровня $$$i + 1$$$ пока не посетит все точки уровня $$$i$$$. Он начинает посещать точки, начиная с минимального уровня точек из заданного множества.
Пусть расстояние между точками $$$(x_1, y_1)$$$ и $$$(x_2, y_2)$$$ равно $$$|x_1 - x_2| + |y_1 - y_2|$$$ где $$$|v|$$$ равно абсолютной величине $$$v$$$.
Максим хочет посетить все ключевые точки таким образом, что суммарная дистанция, которую он пройдет, будет минимально возможной. Ваша задача — найти эту дистанцию.
Если вы программируете на Python, рассмотрите возможность отправки решения на PyPy, а не на Python, когда будете посылать свой код.
Первая строка входных данных содержит одно целое число $$$n$$$ ($$$1 \le n \le 2 \cdot 10^5$$$) — количество ключевых точек.
Каждая из следующих $$$n$$$ строк содержит два целых числа $$$x_i$$$, $$$y_i$$$ ($$$0 \le x_i, y_i \le 10^9$$$) — $$$x$$$-координата ключевой точки $$$p_i$$$ и $$$y$$$-координата ключевой точки $$$p_i$$$. Гарантируется, что все точки различны и точки $$$(0, 0)$$$ нет среди заданных.
Выведите одно целое число — минимально возможную суммарную дистанцию, которую Максим может пройти, если он будет посещать все ключевые точки в порядке, описанном выше.
8
2 2
1 4
2 3
3 1
3 4
1 1
4 3
1 2
15
5
2 1
1 0
2 0
3 2
0 3
9
Картинка, соответствующая первому тестовому примеру: 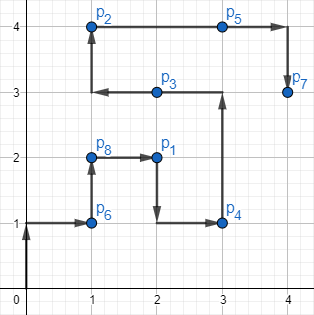
Здесь описан один из возможных ответов длины $$$15$$$.
Картинка, соответствующая второму тестовому примеру: 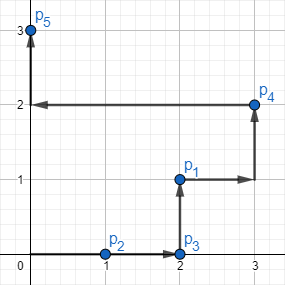
Здесь описан один из возможных ответов длины $$$9$$$.
| Название |
|---|




