Задано неориентированное невзвешенное дерево, состоящее из $$$n$$$ вершин.
Неориентированное дерево — это связный неориентированный граф с $$$n - 1$$$ ребром.
Ваша задача — выбрать две пары вершин этого дерева (все выбранные вершины должны быть различны) $$$(x_1, y_1)$$$ и $$$(x_2, y_2)$$$ таким образом, что $$$x_1$$$ и $$$y_1$$$ не должны принадлежать простому пути от $$$x_2$$$ до $$$y_2$$$ и наоборот ($$$x_2$$$ и $$$y_2$$$ не должны принадлежать простому пути от $$$x_1$$$ до $$$y_1$$$).
Гарантируется, что для заданного дерева всегда возможно выбрать такие пары.
Среди всех возможных способов выбрать эти пары вам необходимо выбрать способ с максимальным количеством общих вершин между путями от $$$x_1$$$ до $$$y_1$$$ и от $$$x_2$$$ до $$$y_2$$$. И среди всех таких пар вам необходимо выбрать пару с максимальной суммарной длиной этих двух путей.
Гарантируется, что для заданного дерева существует ответ, содержащий хотя бы две общие вершины между путями.
Длина пути — это количество ребер в нем.
Простой путь — это путь, посещающий каждую вершину не более одного раза.
Первая строка входных данных содержит одно целое число $$$n$$$ — количество вершин в дереве ($$$6 \le n \le 2 \cdot 10^5$$$).
Каждая из следующих $$$n - 1$$$ строк описывает ребра дерево.
Ребро $$$i$$$ описывается двумя целыми числами $$$u_i$$$ и $$$v_i$$$, номерами вершин, которые оно соединяет ($$$1 \le u_i, v_i \le n$$$, $$$u_i \ne v_i$$$).
Гарантируется, что заданные ребра образуют дерево.
Гарантируется, что для заданного дерева существует ответ, содержащий хотя бы две общие вершины между путями.
Выведите любые две пары вершин, удовлетворяющие ограничениям, описанным в условии задачи.
Гарантируется, что для заданного дерева всегда возможно выбрать такие пары.
7
1 4
1 5
1 6
2 3
2 4
4 7
3 6
7 5
9
9 3
3 5
1 2
4 3
4 7
1 7
4 6
3 8
2 9
6 8
10
6 8
10 3
3 7
5 8
1 7
7 2
2 9
2 8
1 4
10 6
4 5
11
1 2
2 3
3 4
1 5
1 6
6 7
5 8
5 9
4 10
4 11
9 11
8 10
Картинка, соответствующая первому тестовому примеру: 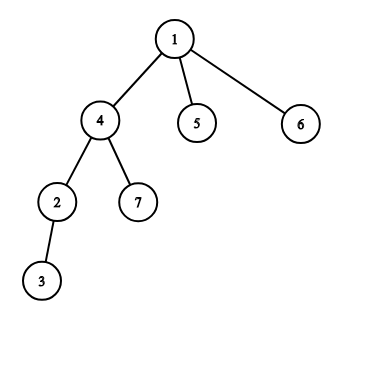
Пересечение путей равно $$$2$$$ (вершины $$$1$$$ и $$$4$$$), а суммарная длина равна $$$4 + 3 = 7$$$.
Картинка, соответствующая второму тестовому примеру: 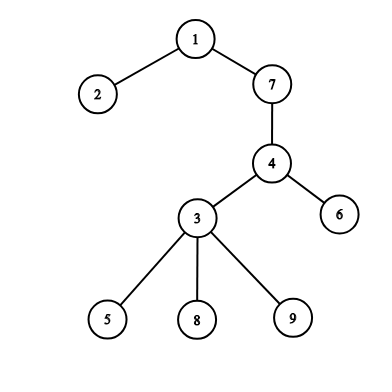
Пересечение путей равно $$$2$$$ (вершины $$$3$$$ и $$$4$$$), а суммарная длина равна $$$5 + 3 = 8$$$.
Картинка, соответствующая третьему тестовому примеру: 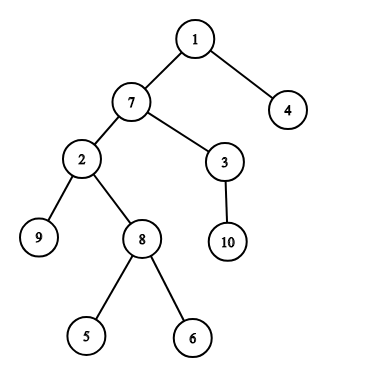
Пересечение путей равно $$$3$$$ (вершины $$$2$$$, $$$7$$$ и $$$8$$$), а суммарная длина равна $$$5 + 5 = 10$$$.
Картинка, соответствующая четвертому тестовому примеру: 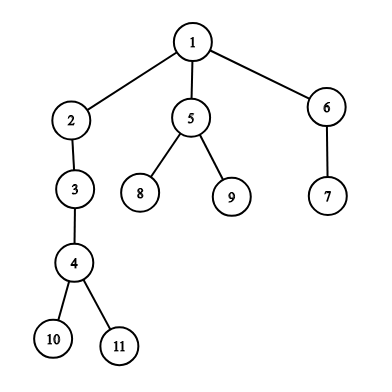
Пересечение путей равно $$$5$$$ (вершины $$$1$$$, $$$2$$$, $$$3$$$, $$$4$$$ и $$$5$$$), а суммарная длина равна $$$6 + 6 = 12$$$.
| Название |
|---|




