| Codeforces Round 524 (Div. 2) |
|---|
| Закончено |
Недавно Оля получила магический квадрат размером $$$2^n\times 2^n$$$.
Её сестре кажется, что один квадрат — это скучно, поэтому она попросила Олю, чтобы та выполнила ровно $$$k$$$ операций разбиения.
Операция разбиения — операция, во время которой Оля берет некий квадрат со стороной $$$a$$$ и разрезает его на 4 равных квадрата со стороной $$$\dfrac{a}{2}$$$. Если сторона квадрата равна $$$1$$$, то к нему нельзя применить операцию разбиения (смотрите примеры для лучшего понимания).
Оля с радостью выполнит просьбу сестры, но она также хочет, чтобы после всех операций соблюдалось условие счастья Оли.
Условие счастья Оли будет соблюдено, если выполняется следующее утверждение:
Пускай длина стороны левого нижнего квадратика равна $$$a$$$, то и длина стороны правого верхнего квадратика тоже должна равняться $$$a$$$. Также должен существовать путь между ними, который состоит только из квадратиков с длиной стороны $$$a$$$. Все последовательные квадраты на пути должны иметь общую сторону.
Очевидно, пока у нас есть один квадрат, то данные условия соблюдаются. Так что Оля готова выполнить просьбу сестры только при условии, что она тоже останется довольна. Скажите ей: возможно ли выполнить ровно $$$k$$$ операций разбиения в некоторой последовательности так, чтобы соблюдалось условие счастья Оли? Если можно, то укажите также то, какой размер будут иметь квадратики из которых будет состоять путь из левого нижнего квадратика в правый верхний.
Первая строка содержит одна целое число $$$t$$$ ($$$1 \le t \le 10^3$$$) — количество тестов.
Каждая из следующих $$$t$$$ строк содержит два целых числа $$$n_i$$$ и $$$k_i$$$ ($$$1 \le n_i \le 10^9, 1 \le k_i \le 10^{18}$$$) — описание $$$i$$$-го теста, которое означает, что исходный квадрат Оли имеет размер $$$2^{n_i}\times 2^{n_i}$$$ и сестра Оли просит сделать ровно $$$k_i$$$ операций разбиения.
Выведите $$$t$$$ строк, где в $$$i$$$-й строке надо вывести «YES» если в $$$i$$$-м тесте можно выполнить $$$k_i$$$ операций разбиения так, чтобы условие счастья Оли соблюдалось или «NO» в противном случае. Если вы вывели «YES», то также выведите $$$log_2$$$ от длины стороны квадратиков, по которым можно будет построить путь из левого нижнего квадратика в правый верхний.
Вы можете выводить каждую букву в любом регистре (строчную или заглавную).
Если существует несколько решений, выведите любое из них.
3 1 1 2 2 2 12
YES 0 YES 1 NO
В каждой из иллюстраций изображения отображаются в порядке, в котором Оля применяла операции. Недавно созданные квадраты выделены красным цветом.
В первом тесте Оля может применять операции разбиения в следующем порядке:
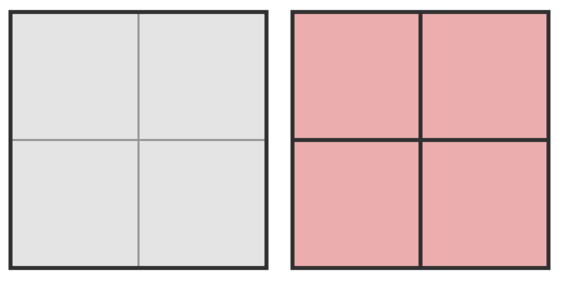
Тогда условие счастья Оли будет соблюдено, так как существует путь из квадратиков одинакового размера от левого нижнего квадратика до правого верхнего:
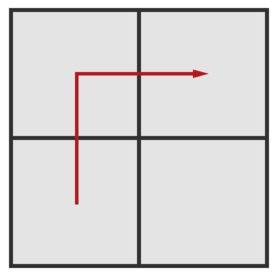
Размер стороны квадратиков на этом пути равен $$$1$$$. $$$log_2(1) = 0$$$.
Во втором тесте Оля может применять операции разбиения в следующем порядке:
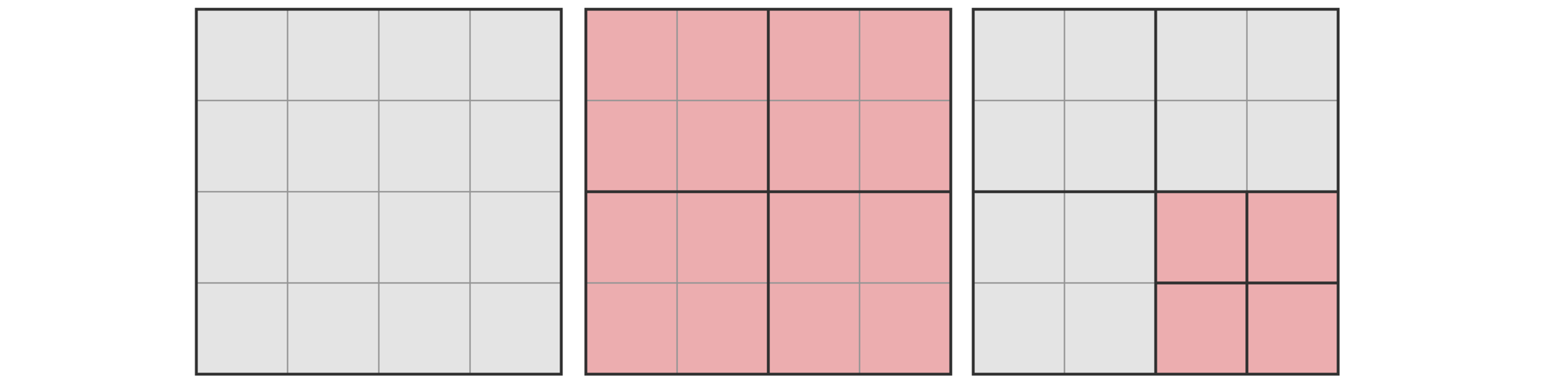
Тогда условие счастья Оли будет соблюдено, так как существует путь из квадратиков одинакового размера от левого нижнего квадратика до правого верхнего:
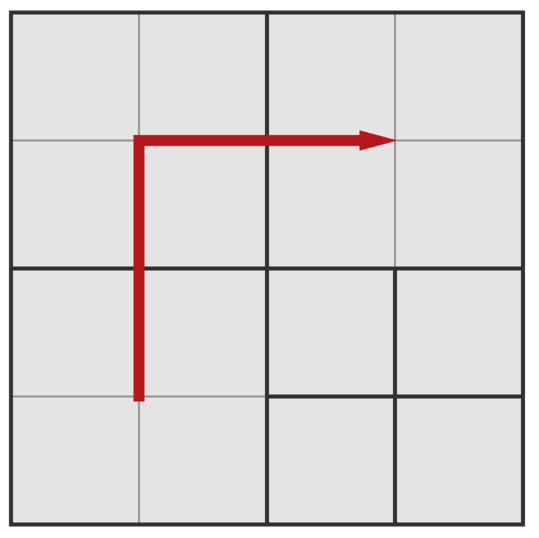
Размер стороны квадратиков на этом пути равен $$$2$$$. $$$log_2(2) = 1$$$.
В третьем примере Оля за $$$5$$$ операций приведет квадратик к следующему виду:
Поскольку ей осталось ещё выполнить $$$7$$$ операций разбиения, а к квадратам со стороной равной $$$1$$$ их применять нельзя, значит Оля не сможет больше ничего сделать и ответ «NO».
| Название |
|---|




