| Codeforces Round 526 (Div. 1) |
|---|
| Закончено |
Однажды Гриша нашёл дерево (связный ациклический граф) с корнем в вершине $$$1$$$.
Но дерево было не простое — в вершинах этого дерева записана перестановка $$$p$$$ чисел от $$$0$$$ до $$$n - 1$$$, в $$$i$$$-й вершине записано число $$$p_i$$$.
Так как Гриша любит придумывать себе странные и интересные задачи, но не всегда с ними справляется, вам нужно помочь ему обработать два типа запросов на этом дереве.
Определим функцию $$$MEX(S)$$$, где $$$S$$$ является множеством целых неотрицательных чисел, как наименьшее целое неотрицательное число, не входящее в множество.
Пусть $$$l$$$ — простой путь в дереве. Тогда обозначим за $$$u_1$$$, $$$u_2$$$, $$$\ldots$$$, $$$u_k$$$ — номера вершин, принадлежащих $$$l$$$.
Обозначим за $$$V(l)$$$ множество {$$$p_{u_1}$$$, $$$p_{u_2}$$$, $$$\ldots$$$ , $$$p_{u_k}$$$}.
Тогда запросы таковы:
- Для двух вершин $$$i$$$ и $$$j$$$ нужно поменять местами значения $$$p_i$$$ и $$$p_j$$$.
- Требуется найти максимальный $$$MEX(V(l))$$$ по все возможным $$$l$$$.
Первая строка содержит одно целое число $$$n$$$ ($$$2 \leq n \leq 2 \cdot 10^5$$$) — количество вершин в дереве.
Вторая строка содержит $$$n$$$ целых чисел $$$p_1$$$, $$$p_2$$$, $$$\ldots$$$, $$$p_n$$$ ($$$0\leq p_i < n$$$) — перестановка $$$p$$$. Гарантируется, что все числа различны.
Третья строка содержит $$$n - 1$$$ целое число $$$d_2$$$, $$$d_3$$$, $$$\ldots$$$, $$$d_n$$$ ($$$1 \leq d_i < i$$$), где $$$d_i$$$ — непосредственный предок вершины $$$i$$$ в дереве.
Четвёртая строка содержит одно целое число $$$q$$$ ($$$1 \leq q \leq 2 \cdot 10^5$$$) — количество запросов.
Следующие $$$q$$$ строк содержат описание запросов:
Каждая из следующих $$$q$$$ строк содержит одно целое число $$$t$$$ ($$$1$$$ или $$$2$$$) — тип запроса.
- Если $$$t = 1$$$, далее следуют два целых числа $$$i$$$ и $$$j$$$ ($$$1 \leq i, j \leq n$$$) — номера вершин, значения перестановки в которых нужно поменять местами.
- Если же $$$t = 2$$$, нужно найти максимальный $$$MEX(V(l))$$$ по все возможным $$$l$$$.
Для каждого запроса второго типа выведите единственное число — ответ на запрос.
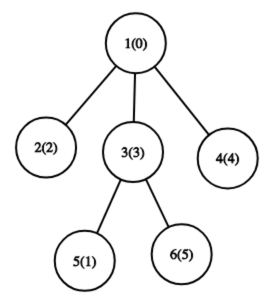
6 2 5 0 3 1 4 1 1 3 3 3 3 2 1 6 3 2
3 2
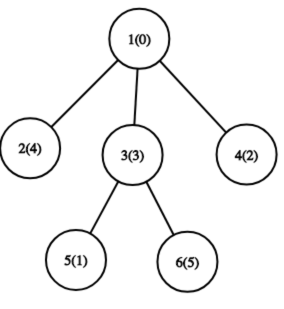
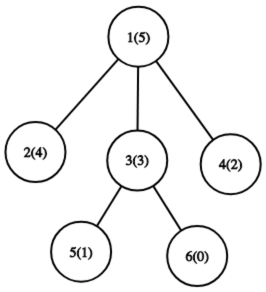
6 5 2 1 4 3 0 1 1 1 3 3 9 2 1 5 3 2 1 6 1 2 1 4 2 2 1 1 6 2
3 2 4 4 2
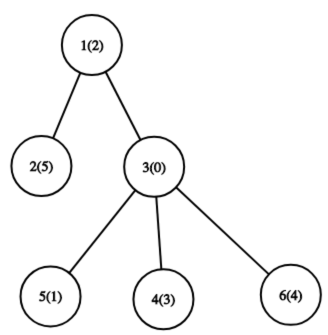
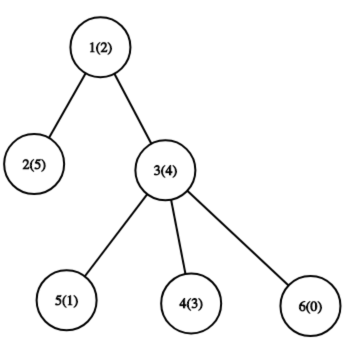
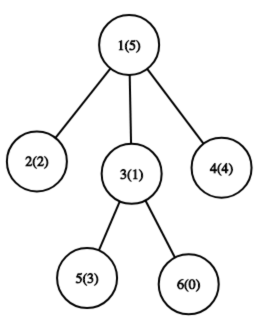
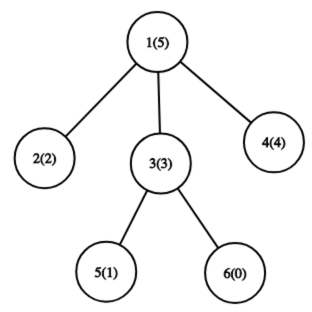
Число в скобках обозначает значение перестановки для вершины.
| Название |
|---|




