| Codeforces Round 525 (Div. 2) |
|---|
| Закончено |
Дано дерево, состоящее из $$$n$$$ вершин. У каждой вершины $$$u$$$ есть вес $$$a_u$$$. Гарантируется, что в дереве есть только одна вершина с минимальным весом. У каждой вершины $$$u$$$ (кроме вершины с минимальным $$$a_u$$$), есть сосед $$$v$$$, такой, что $$$a_v<a_u$$$.
Вам необходимо составить дерево с минимальным весом $$$w$$$, который считается следующим образом:
- Для каждой вершины $$$u$$$, $$$deg_u \cdot a_u$$$ прибавляется к $$$w$$$ ($$$deg_u$$$ обозначает степень вершины $$$u$$$).
- Для каждого ребра $$$\{ u,v \}$$$, $$$\lceil log_2(dist(u,v)) \rceil \cdot min(a_u,a_v)$$$ прибавляется к $$$w$$$, где $$$dist(u,v)$$$ обозначает количество ребер на пути из $$$u$$$ в $$$v$$$ в данном дереве.
В первой строке записано одно целое число $$$n$$$ $$$(2 \le n \le 5 \cdot 10^5)$$$, количество вершин в дереве.
Во второй строке записаны $$$n$$$ целых чисел $$$a_1, a_2, \ldots, a_n$$$ $$$(1 \le a_i \le 10^9)$$$, веса вершин дерева.
Далее следует $$$n-1$$$ строка, в каждой из которых записаны по два целых числа $$$u$$$ и $$$v$$$ $$$(1 \le u,v \le n)$$$. Это означает, что между $$$u$$$ и $$$v$$$ есть ребро в данном дереве.
Выведите одно целое число: минимальное возможное значение $$$w$$$.
3
1 2 3
1 2
1 3
7
5
4 5 3 7 8
1 2
1 3
3 4
4 5
40
В первом примере данное дерево исходно имеет минимальное значение $$$w$$$.
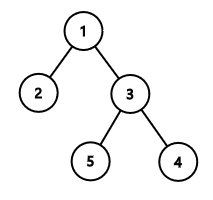
Во втором примере оптимальное дерево имеет следующий вид:
| Название |
|---|




