| Codeforces Beta Round 84 (Div. 1 Only) |
|---|
| Закончено |
Петя любит счастливые числа. Всем известно, что счастливыми являются положительные целые числа, в десятичной записи которых содержатся только счастливые цифры 4 и 7. Например, числа 47, 744, 4 являются счастливыми, а 5, 17, 467 — не являются.
Петя и его друг Вася играют в интересную игру. Петя выбирает случайным образом целое число p из отрезка [pl, pr], а Вася — целое число v из отрезка [vl, vr] (также случайно). Оба игрока выбирают числа равновероятно. Найдите вероятность того, что количество счастливых чисел на отрезке [min(v, p), max(v, p)] ровно k.
В единственной строке задано пять целых чисел pl, pr, vl, vr и k (1 ≤ pl ≤ pr ≤ 109, 1 ≤ vl ≤ vr ≤ 109, 1 ≤ k ≤ 1000).
В единственной строке выведите результат с абсолютной погрешностью не более 10 - 9.
1 10 1 10 2
0.320000000000
5 6 8 10 1
1.000000000000
Считайте, что [a, b] обозначает отрезок целых чисел, включающий границы. То есть 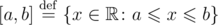
В первом примере есть 32 подходящих пар чисел: (1, 7), (1, 8), (1, 9), (1, 10), (2, 7), (2, 8), (2, 9), (2, 10), (3, 7), (3, 8), (3, 9), (3, 10), (4, 7), (4, 8), (4, 9), (4, 10), (7, 1), (7, 2), (7, 3), (7, 4), (8, 1), (8, 2), (8, 3), (8, 4), (9, 1), (9, 2), (9, 3), (9, 4), (10, 1), (10, 2), (10, 3), (10, 4). Количество всех возможных исходов равно 10·10 = 100. Поэтому ответ: 32 / 100.
Во втором примере число Пети всегда меньше чем число Васи, а счастливое 7 всегда между их результатами, поэтому при любом выборе чисел одно счастливое число будет в интервале.
| Название |
|---|




