| Codeforces Round 527 (Div. 3) |
|---|
| Закончено |
Задано дерево, состоящее ровно из $$$n$$$ вершин. Дерево — это связный неориентированный граф с $$$n-1$$$ ребром. Каждой вершине $$$v$$$ этого дерева соответствует некоторое значение $$$a_v$$$.
Пусть $$$dist(x, y)$$$ — расстояние между вершинами $$$x$$$ и $$$y$$$. Расстояние между вершинами — это количество ребер на простом пути между ними.
Определим стоимость дерева как следующую величину: сначала давайте зафиксируем одну вершину дерева. Пусть она равна $$$v$$$. Тогда стоимость дерева равна $$$\sum\limits_{i = 1}^{n} dist(i, v) \cdot a_i$$$.
Ваша задача — найти максимально возможную стоимость дерева, если вы можете выбирать $$$v$$$ самостоятельно.
Первая строка входных данных содержит одно целое число $$$n$$$, количество вершин в дереве ($$$1 \le n \le 2 \cdot 10^5$$$).
Вторая строка входных данных содержит $$$n$$$ целых чисел $$$a_1, a_2, \dots, a_n$$$ ($$$1 \le a_i \le 2 \cdot 10^5$$$), где $$$a_i$$$ равно значению вершины $$$i$$$.
Каждая из следующих $$$n - 1$$$ строк описывает ребра дерева. Ребро $$$i$$$ описывается двумя целыми числами $$$u_i$$$ и $$$v_i$$$, номерами вершин, которые оно соединяет ($$$1 \le u_i, v_i \le n$$$, $$$u_i \ne v_i$$$).
Гарантируется, что заданные ребра образуют дерево.
Выведите одно целое число — максимально возможную стоимость дерева, если вы можете выбрать любую вершину в качестве вершины $$$v$$$.
8 9 4 1 7 10 1 6 5 1 2 2 3 1 4 1 5 5 6 5 7 5 8
121
1 1337
0
Картинка, соответствующая первому тестовому примеру: 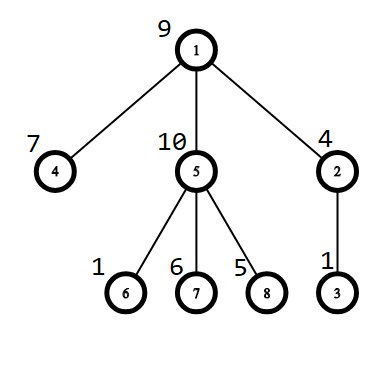
Вы можете выбрать вершину $$$3$$$ как корень, тогда ответ будет равен $$$2 \cdot 9 + 1 \cdot 4 + 0 \cdot 1 + 3 \cdot 7 + 3 \cdot 10 + 4 \cdot 1 + 4 \cdot 6 + 4 \cdot 5 = 18 + 4 + 0 + 21 + 30 + 4 + 24 + 20 = 121$$$.
Во втором тестовом примере дерево состоит только из одной вершины, поэтому ответ всегда равен $$$0$$$.
| Название |
|---|




