| Codeforces Round 530 (Div. 1) |
|---|
| Закончено |
Погуляв по заснеженному лесу, Миша очень полюбил деревья и решил нарисовать своё!
Это дерево состоит из $$$n$$$ вершин, пронумерованных различными целыми числами от $$$1$$$ до $$$n$$$. В этом дереве вершина $$$1$$$ является корнем, а у любой другой вершины $$$i$$$ есть непосредственный предок $$$p_{i}$$$ (при этом $$$i$$$ — непосредственный потомок $$$p_{i}$$$).
Вершина $$$u$$$ лежит в поддереве вершины $$$v$$$, если переходя по непосредственным предкам из вершины $$$u$$$ ($$$u$$$, $$$p_{u}$$$, $$$p_{p_{u}}$$$, ...), можно попасть в вершину $$$v$$$. В частности, любая вершина $$$v$$$ лежит в поддереве самой себя. Число вершин в поддереве вершины $$$v$$$ называется размером поддерева. Миша рассматривает только те деревья, в которых все вершины лежат в поддереве вершины $$$1$$$.
На рисунке ниже изображено дерево из $$$6$$$ вершин. Поддерево вершины $$$2$$$ состоит из вершин $$$2$$$, $$$3$$$, $$$4$$$, $$$5$$$. Таким образом, размер поддерева этой вершины равен $$$4$$$.
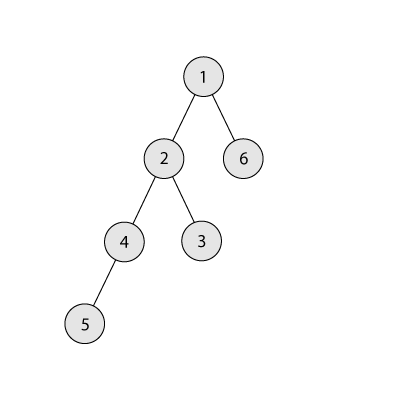
Назовём разветвлённостью дерева максимальное количество непосредственных потомков какой-то из его вершин. Так, разветвлённость дерева на рисунке выше равна 2. Помогите Мише построить дерево из $$$n$$$ вершин, в котором сумма размеров всех поддеревьев равна в точности $$$s$$$, а разветвлённость — минимально возможная.
В первой и единственной строке входных данных записаны два целых числа $$$n$$$ и $$$s$$$ — число вершин в дереве и требуемая сумма размеров поддеревьев ($$$2 \le n \le 10^5$$$; $$$1 \le s \le 10^{10}$$$).
Если требуемого дерева не существует, выведите «No». Иначе в первой строке выходных данных выведите «Yes», а в следующей строке выведите числа $$$p_2$$$, $$$p_3$$$, ..., $$$p_n$$$, где вершина с номером $$$p_i$$$ является непосредственным предком вершины с номером $$$i$$$.
3 5
Yes 1 1
4 42
No
6 15
Yes 1 2 3 1 5
Для первого примера одним из оптимальных деревьев изображено ниже. Сумма размеров поддеревьев в этом дереве равна $$$3 + 1 + 1 = 5$$$, а разветвлённость равна $$$2$$$.
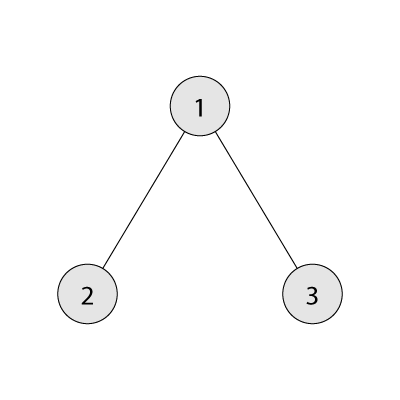
Для третьего примера одним из оптимальных деревьев изображено ниже. В этом дереве сумма размеров поддеревьев равна $$$6 + 3 + 2 + 1 + 2 + 1 = 15$$$, а разветвлённость равна $$$2$$$.
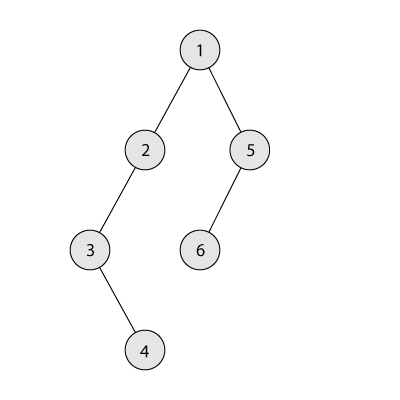
| Название |
|---|




