| Codeforces Round 539 (Div. 1) |
|---|
| Закончено |
Федя — друг Саши, поэтому Саша знает о Феде всё.
Федя хранит своё терпение в бесконечно большой чаше. Терпение Феди, в отличие от чаши, не бесконечно, поэтому обозначим за $$$v$$$ — количество литров терпения в чаше Феди и, как только $$$v$$$ станет равно $$$0$$$, чаша сразу же лопнет. В чаше существует один кран, который закачивает по $$$s$$$ литров терпения за одну секунду. Заметим, что $$$s$$$ может быть отрицательным, в этом случае кран откачивает терпение из чаши. Саша может делать разные вещи, поэтому ему посильно изменять пропускную способность крана. Все действия Саши можно представить в виде $$$q$$$ запросов. Запросы бывают трёх типов:
- «1 t s» — добавить новое событие, которое означает, что начиная с секунды $$$t$$$, пропускная способность крана станет равна $$$s$$$.
- «2 t» — удалить событие, которое происходит в секунду $$$t$$$. Гарантируется, что оно существует.
- «3 l r v» — Саше интересно, если взять все ещё не удалённые события, для которых верно $$$l \le t \le r$$$, а затем промоделировать изменение терпения Феди с начала секунды $$$l$$$ до начала секунды $$$r$$$ включительно (начальный объем терпения, в начале секунды $$$l$$$, равен $$$v$$$ литров), то в какой момент времени чаша лопнет. Если чаша никогда не лопнет, ответом на запрос будет одно целое число $$$-1$$$.
Так как Саша не хочет проверять, что случится, когда терпение Феди закончится, а запросы он уже придумал, то он попросил вас помочь ему и для каждого запроса $$$3$$$-го типа найти ответ.
Гарантируется, что никогда не будет одновременно существовать два события, происходящих в одну и ту же секунду.
Первая строка содержит одно целое число $$$q$$$ ($$$1 \le q \le 10^5$$$) — количество запросов.
Каждая из последующих $$$q$$$ строк имеет один из форматов:
- 1 t s ($$$1 \le t \le 10^9$$$, $$$-10^9 \le s \le 10^9$$$), означающий, что добавляется новое событие, которое означает что начиная с секунды $$$t$$$ пропускная способность крана станет равна $$$s$$$.
- 2 t ($$$1 \le t \le 10^9$$$), означающий, что нужно удалить событие, происходящее в момент времени $$$t$$$. Гарантируется, что среди ещё не удалённых такое существует.
- 3 l r v ($$$1 \le l \le r \le 10^9$$$, $$$0 \le v \le 10^9$$$), означающий, что нужно промоделировать процесс с момента начала секунды $$$l$$$ до начала секунды $$$r$$$ и сказать когда чаша лопнет.
Гарантируется что $$$t$$$, $$$s$$$, $$$l$$$, $$$r$$$, $$$v$$$ во всех запросах — целые числа.
Гарантируется, что есть хотя бы один запрос $$$3$$$-го типа, а также не может быть запроса $$$1$$$-го типа с таким $$$t$$$, что существует событие с аналогичным значением $$$t$$$ и оно ещё не удалено.
Для каждого запроса $$$3$$$-го типа в отдельной строке выведите момент времени, когда чаша лопнет или $$$-1$$$, если такого не случится.
Ваш ответ будет считаться правильным, если его абсолютная или относительная ошибка не превосходит $$$10^{-6}$$$.
Формально, пусть ваш ответ равен $$$a$$$, а ответ жюри равен $$$b$$$. Ваш ответ будет зачтен, если и только если $$$\frac{|a - b|}{\max{(1, |b|)}} \le 10^{-6}$$$.
6 1 2 1 1 4 -3 3 1 6 1 3 1 6 3 3 1 6 4 3 1 6 5
5 5.666667 6 -1
10 1 2 2 1 4 4 1 7 -10 3 2 4 1 3 5 6 0 3 1 15 1 2 4 3 1 15 1 1 8 1 3 1 15 1
-1 5 8.7 8.1 -1
5 1 1000 9999999 1 2000 -9999 3 1000 2000 0 2 1000 3 1000 2002 1
1000 2000.0001
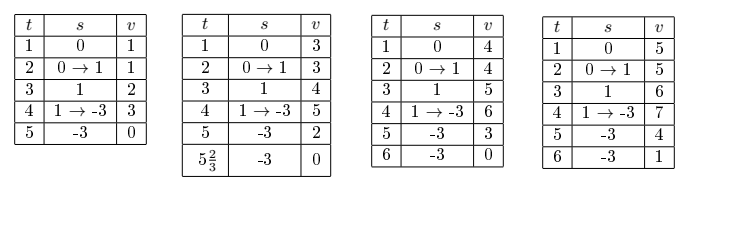
В первом примере все события попадают во все запросы $$$3$$$-го типа, а их моделирование выглядит следующим образом:
| Название |
|---|




