| Codeforces Round 539 (Div. 1) |
|---|
| Закончено |
Однажды Саша решил, как обычно, прогуляться по парку. Придя в парк он обнаружил, что его любимая скамейка уже занята, и ему пришлось присесть на соседнюю. Саша сел и начал вслушиваться в тишину. Тут ему в голову пришла мысль: а что если в разных частях парка тишина звучит по-разному? Так и оказалось. Разделим парк на квадраты размера $$$1 \times 1$$$ метр и назовем их клетками, пронумеруем строки от $$$1$$$ до $$$n$$$ сверху вниз, а столбцы от $$$1$$$ до $$$m$$$ слева направо. Теперь любую клетку можно описать парой чисел $$$(x, y)$$$, где $$$x$$$ — номер строки, а $$$y$$$ — номер столбца, в котором расположена эта клетка. Опытным путём Саша выяснил, что в клетке $$$(i, j)$$$ громкость тишины равна $$$f_{i,j}$$$, а также все $$$f_{i,j}$$$ образуют перестановку чисел от $$$1$$$ до $$$n \cdot m$$$. Саша решил посчитать, а сколько существует приятных отрезков тишины?
Возьмем какой-то отрезок $$$[l \ldots r]$$$. Обозначим за $$$S$$$ множество клеток $$$(i, j)$$$, что $$$l \le f_{i,j} \le r$$$. Тогда отрезок тишины $$$[l \ldots r]$$$ является приятным, если существует только один простой путь между каждой парой клеток из $$$S$$$ (путь не может содержать клетки, которые не содержатся в $$$S$$$). Другими словами, множество $$$S$$$ должно выглядеть на плоскости как дерево. Саша справился с этим заданием очень быстро и назвал алгоритм — «алгоритмом звуков тишины».
Время шло, и от алгоритма осталась только легенда. Чтобы доказать правдивость истории, вам предстоит помочь Саше и посчитать количество различных приятных отрезков тишины. Два отрезка $$$[l_1 \ldots r_1]$$$, $$$[l_2 \ldots r_2]$$$ считаются различными, если $$$l_1 \neq l_2$$$ или $$$r_1 \neq r_2$$$ или и то, и то одновременно.
Первая строка содержит два целых числа $$$n$$$ и $$$m$$$ ($$$1 \le n, m \le 1000$$$, $$$1 \le n \cdot m \le 2 \cdot 10^5$$$) — размеры парка.
Каждая из следующих $$$n$$$ строк содержит по $$$m$$$ целых чисел $$$f_{i,j}$$$ ($$$1 \le f_{i,j} \le n \cdot m$$$) — громкость тишины в клетке $$$(i, j)$$$.
Гарантируется, что все $$$f_{i,j}$$$ различны.
Выведите одно число — количество приятных отрезков тишины.
1 5
1 2 3 4 5
15
2 3
1 2 3
4 5 6
15
4 4
4 3 2 16
1 13 14 15
5 7 8 12
6 11 9 10
50
В первом примере все отрезки тишины приятные.
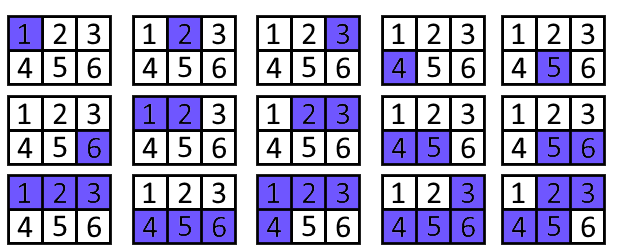
Во втором примере приятными являются следующие отрезки тишины:
| Название |
|---|




