F2. Разрезание дерева (сложная версия)
ограничение по времени на тест
2 секунды
ограничение по памяти на тест
256 мегабайт
ввод
стандартный ввод
вывод
стандартный вывод

Задано неориентированное дерево из $$$n$$$ вершин.

Некоторые вершины покрашены в один из $$$k$$$ цветов, а некоторые не покрашены совсем. Гарантируется, что дерево содержит хотя бы одну вершину каждого из $$$k$$$ цветов. Может быть ноль непокрашенных вершин.

Вы выбираете набор из ровно $$$k - 1$$$ ребер и удаляете его из дерева. Дерево распадается на $$$k$$$ связных компонент. Назовем набор хорошим, если ни в одной из полученных компонент не будет вершин различных цветов.

Сколько хороших наборов ребер есть в данном дереве? Два набора считаются различными, если существует такое ребро, что оно присутствует в одном наборе и отсутствует в другом.

Ответ может быть довольно большим, поэтому выведите его по модулю $$$998244353$$$.

Входные данные

В первой строке записаны два целых числа $$$n$$$ и $$$k$$$ ($$$2 \le n \le 3 \cdot 10^5$$$, $$$2 \le k \le n$$$) — количество вершин в дереве и количество цветов, соответственно.

Во второй строке записаны $$$n$$$ целых чисел $$$a_1, a_2, \dots, a_n$$$ ($$$0 \le a_i \le k$$$) — цвета вершин. $$$a_i = 0$$$ значит, что вершина $$$i$$$ не покрашена, любое другое число значит, что вершина $$$i$$$ покрашена в этот цвет.

В $$$i$$$-й из следующих $$$n - 1$$$ строк содержится два целых числа $$$v_i$$$ и $$$u_i$$$ ($$$1 \le v_i, u_i \le n$$$, $$$v_i \ne u_i$$$) — ребра дерева. Гарантируется, что данные ребра образуют дерево. Гарантируется, что дерево содержит хотя бы одну вершину каждого из $$$k$$$ цветов. Может быть ноль непокрашенных вершин.

Выходные данные

Выведите одно целое число — количество хороших наборов ребер в данном дереве. Два набора считаются различными, если существует такое ребро, что оно присутствует в одном наборе и отсутствует в другом.

Ответ может быть довольно большим, поэтому выведите его по модулю $$$998244353$$$.

Примеры
Входные данные
5 2
2 0 0 1 2
1 2
2 3
2 4
2 5
Выходные данные
1
Входные данные
7 3
0 1 0 2 2 3 0
1 3
1 4
1 5
2 7
3 6
4 7
Выходные данные
4
Примечание

Дерево из первого примера:

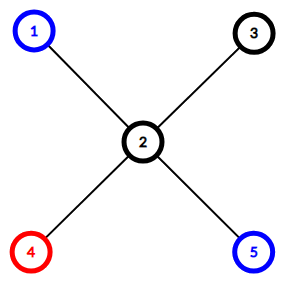
Единственный хороший набор — это ребро $$$(2, 4)$$$. После его удаления дерево распадается на компоненты $$$\{4\}$$$ и $$$\{1, 2, 3, 5\}$$$. В первой компоненте есть только вершина цвета $$$1$$$, а во второй — только вершины цвета $$$2$$$ и непокрашенные вершины.

Дерево из второго примера:

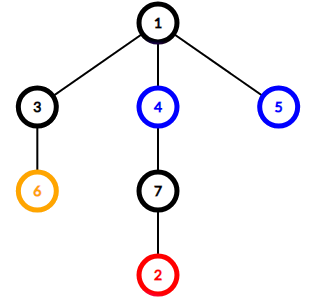
Хорошие наборы: $$$\{(1, 3), (4, 7)\}$$$, $$$\{(1, 3), (7, 2)\}$$$, $$$\{(3, 6), (4, 7)\}$$$ и $$$\{(3, 6), (7, 2)\}$$$.