| Codeforces Round 544 (Div. 3) |
|---|
| Закончено |
Задан неориентированный невзвешенный связный граф, состоящий из $$$n$$$ вершин и $$$m$$$ ребер. Гарантируется, что в графе отсутствуют петли и кратные ребра.
Ваша задача — найти любое такое покрывающее дерево этого графа, что степень первой вершины (вершины с номером $$$1$$$) вершины равна $$$D$$$ (или сказать, что таких покрывающих деревьев не существует). Напомним, что степень вершины — это количество ребер, инцидентных ей.
Первая строка входных данных содержит три целых числа $$$n$$$, $$$m$$$ и $$$D$$$ ($$$2 \le n \le 2 \cdot 10^5$$$, $$$n - 1 \le m \le min(2 \cdot 10^5, \frac{n(n-1)}{2}), 1 \le D < n$$$) — количество вершин, количество ребер и необходимая степень первой вершины соответственно.
Следующие $$$m$$$ строк описывают ребра: ребро $$$i$$$ представлено в виде пары целых чисел $$$v_i$$$, $$$u_i$$$ ($$$1 \le v_i, u_i \le n$$$, $$$u_i \ne v_i$$$), которые означают номера вершин, соединяемых этим ребром. В заданном графе отсутствуют петли и кратные ребра, то есть для каждой пары ($$$v_i, u_i$$$) в списке ребер не существует других пар ($$$v_i, u_i$$$) или ($$$u_i, v_i$$$), также для каждой пары $$$(v_i, u_i)$$$ выполняется условие $$$v_i \ne u_i$$$.
Если не существует покрывающего дерева, удовлетворяющего условию задачи выведите «NO» в первой строке.
Иначе выведите «YES» в первой строке и затем выведите $$$n-1$$$ строк, описывающих ребра такого покрывающего дерева, что степень первой вершины (вершины с номером $$$1$$$) равна $$$D$$$. Убедитесь, что ребра выводимого покрывающего дерева представляют собой подмножество ребер входных данных (порядок ребер не важен, также ребро $$$(v, u)$$$ может быть выведено как $$$(u, v)$$$).
Если существует несколько возможных ответов, выведите любой.
4 5 1 1 2 1 3 1 4 2 3 3 4
YES 2 1 2 3 3 4
4 5 3 1 2 1 3 1 4 2 3 3 4
YES 1 2 1 3 4 1
4 4 3 1 2 1 4 2 3 3 4
NO
Картинка, соответствующая первому и второму тестовым примерам: 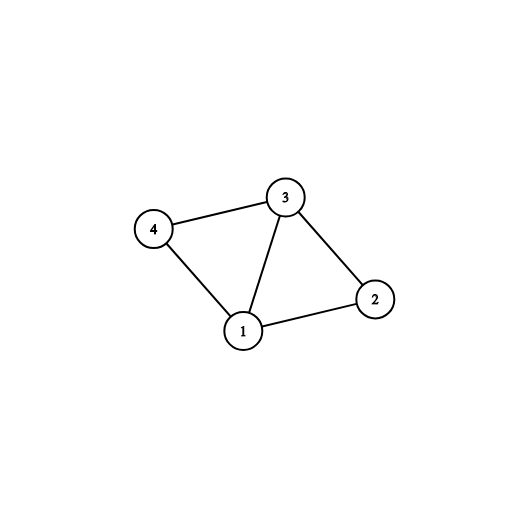
Картинка, соответствующая третьему тестовому примеру: 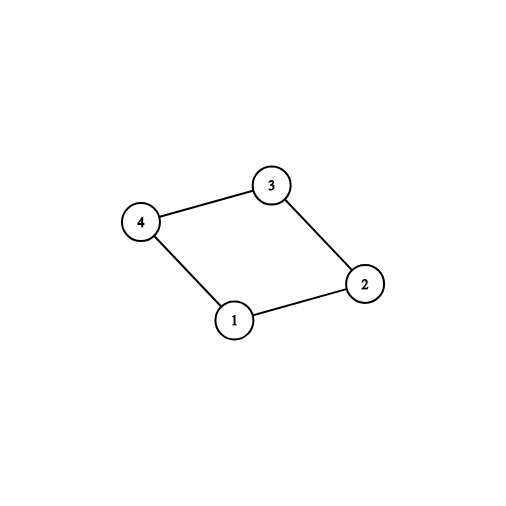
| Название |
|---|




