| Codeforces Round 548 (Div. 2) |
|---|
| Закончено |
Вам дано дерево (связный неориентированный граф без циклов), состоящее из $$$n$$$ вершин. Каждое из $$$n - 1$$$ рёбер дерева покрашено в чёрный или красный цвет.
Вам также дано целое число $$$k$$$. Рассмотрим последовательности из $$$k$$$ вершин. Скажем, что последовательность $$$[a_1, a_2, \ldots, a_k]$$$ является хорошей, если она удовлетворяет следующему:
- Мы пройдём некоторый путь в дереве (возможно посещающий несколько раз одну и ту же вершину или ребро), начинающийся в $$$a_1$$$ и заканчивающийся в $$$a_k$$$.
- Начнём в $$$a_1$$$, затем перейдём в $$$a_2$$$ по кратчайшему пути между $$$a_1$$$ и $$$a_2$$$, затем перейдём в $$$a_3$$$ аналогичным образом, и так далее, пока наконец не пройдём кратчайший путь из $$$a_{k-1}$$$ в $$$a_k$$$.
- Если в результате такого процесса мы пройдём хотя бы по одному чёрному ребру, то последовательность является хорошей.
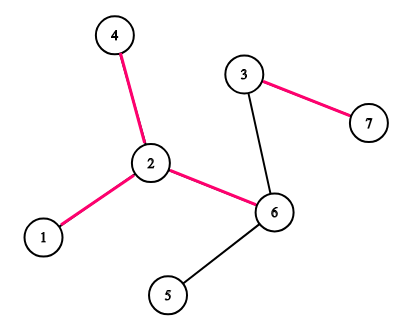
Рассмотрим дерево, изображенное на рисунке. Если $$$k=3$$$, то следующие последовательности являются хорошими: $$$[1, 4, 7]$$$, $$$[5, 5, 3]$$$ и $$$[2, 3, 7]$$$. Следующие последовательности не являются хорошими: $$$[1, 4, 6]$$$, $$$[5, 5, 5]$$$, $$$[3, 7, 3]$$$.
Всего есть $$$n^k$$$ последовательностей вершин, посчитайте сколько из них являются хорошими. Так как это число может быть очень большим, выведите его по модулю $$$10^9+7$$$.
Первая строка содержит два целых числа $$$n$$$ и $$$k$$$ ($$$2 \le n \le 10^5$$$, $$$2 \le k \le 100$$$), — размер дерева и длина последовательности вершин.
Каждая из следующих $$$n - 1$$$ строк содержит три целых числа $$$u_i$$$, $$$v_i$$$ и $$$x_i$$$ ($$$1 \le u_i, v_i \le n$$$, $$$x_i \in \{0, 1\}$$$) — где $$$u_i$$$ и $$$v_i$$$ задают концы соответствующего ребра, а $$$x_i$$$ задаёт его цвет ($$$0$$$ обозначает красное ребро, а $$$1$$$ чёрное).
Выведите одно число — количество хороших последовательностей по модулю $$$10^9 + 7$$$.
4 4 1 2 1 2 3 1 3 4 1
252
4 6 1 2 0 1 3 0 1 4 0
0
3 5 1 2 1 2 3 0
210
В первом примере все последовательности ($$$4^4$$$) длины $$$4$$$ являются хорошими, кроме следующих:
- $$$[1, 1, 1, 1]$$$
- $$$[2, 2, 2, 2]$$$
- $$$[3, 3, 3, 3]$$$
- $$$[4, 4, 4, 4]$$$
Во втором примере, все рёбра красные, а значит нет ни одной хорошей последовательности.
| Название |
|---|




