| Codeforces Round 549 (Div. 1) |
|---|
| Закончено |
Недавно Вася узнал, что через любые две точки на плоскости с различными $$$x$$$ координатами можно провести одну и только одну параболу, уравнение которой будет иметь вид $$$y = x^2 + bx + c$$$, где $$$b$$$ и $$$c$$$ — действительные числа. Назовём такую параболу $$$U$$$-образной.
После этого он нарисовал на плоскости несколько различных точек с целыми координатами и через каждые две из них, имеющие различные координаты $$$x$$$, провёл $$$U$$$-образную параболу. Рисунок получился откровенно плохой, но Вася не теряет надежды найти число различных получившихся парабол, во внутренней области каждой из которых нет ни одной нарисованной точки. Помогите Васе.
Внутренней областью $$$U$$$-образной параболы в данной задаче называется часть плоскости, лежащая строго выше параболы, при этом ось $$$y$$$ направлена вверх.
В первой строке находится единственное целое число $$$n$$$ ($$$1 \le n \le 100\,000$$$) — число точек.
В следующих $$$n$$$ строках находятся описания точек, в $$$i$$$-й из них находятся 2 целых числа $$$x_i$$$ и $$$y_i$$$ — координаты $$$i$$$-й точки. Гарантируется, что все точки различные, а так же что координаты по модулю не превосходят $$$10^6$$$.
В единственной строке выведите единственное число — количество $$$U$$$-образных парабол, проходящих хотя бы через 2 точки и не содержащих никаких других точек в своей внутренней области (не считая границы).
3 -1 0 0 2 1 0
2
5 1 0 1 -1 0 -1 -1 0 -1 -1
1
На двух картинках ниже нарисованы все $$$U$$$-образные параболы, проходящие хотя-бы через 2 отмеченные точки в каждом из двух примеров. Красным отмечены те $$$U$$$-образные параболы, во внутренней области которых нет ни одной точки.
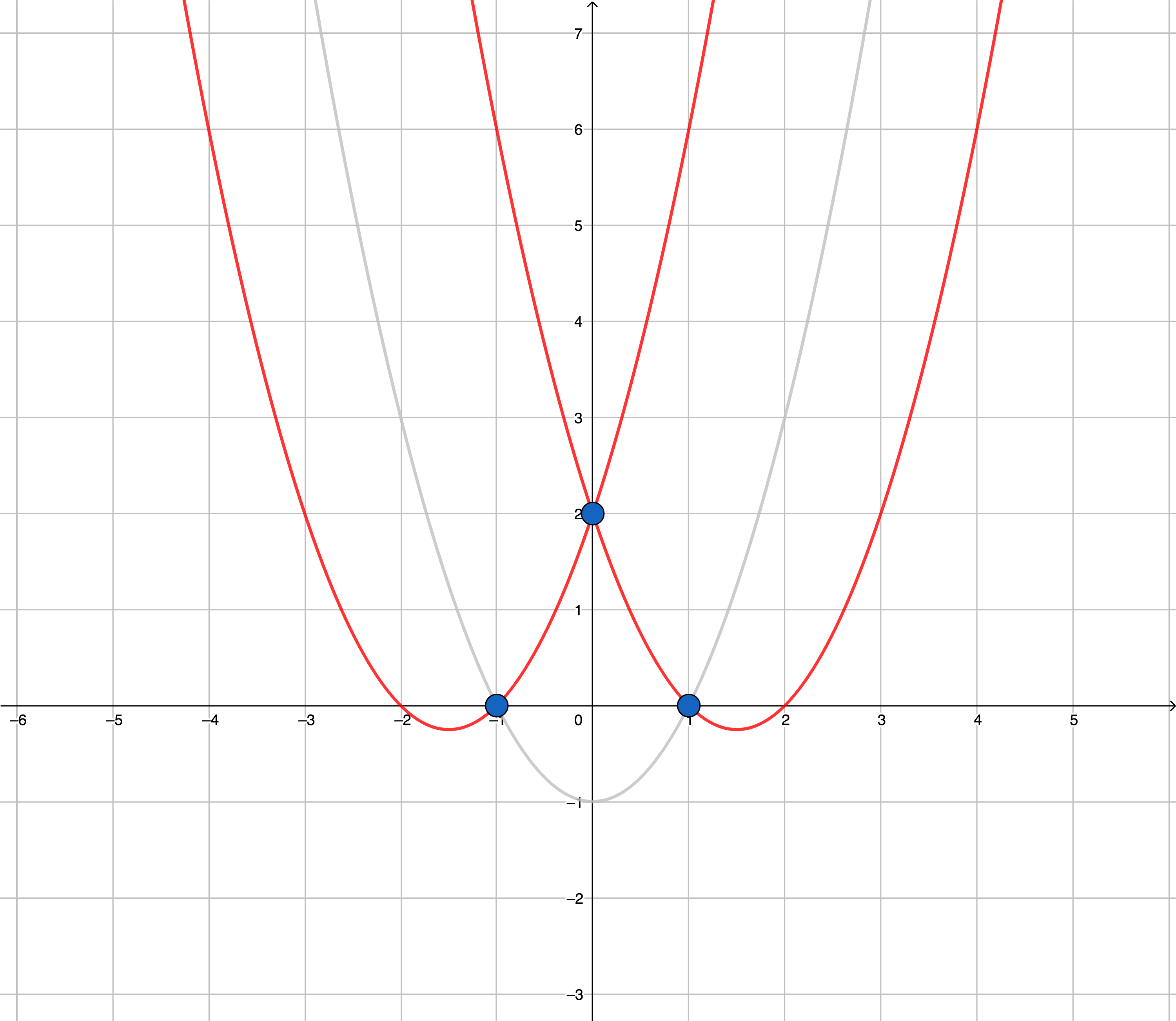Первый пример. 
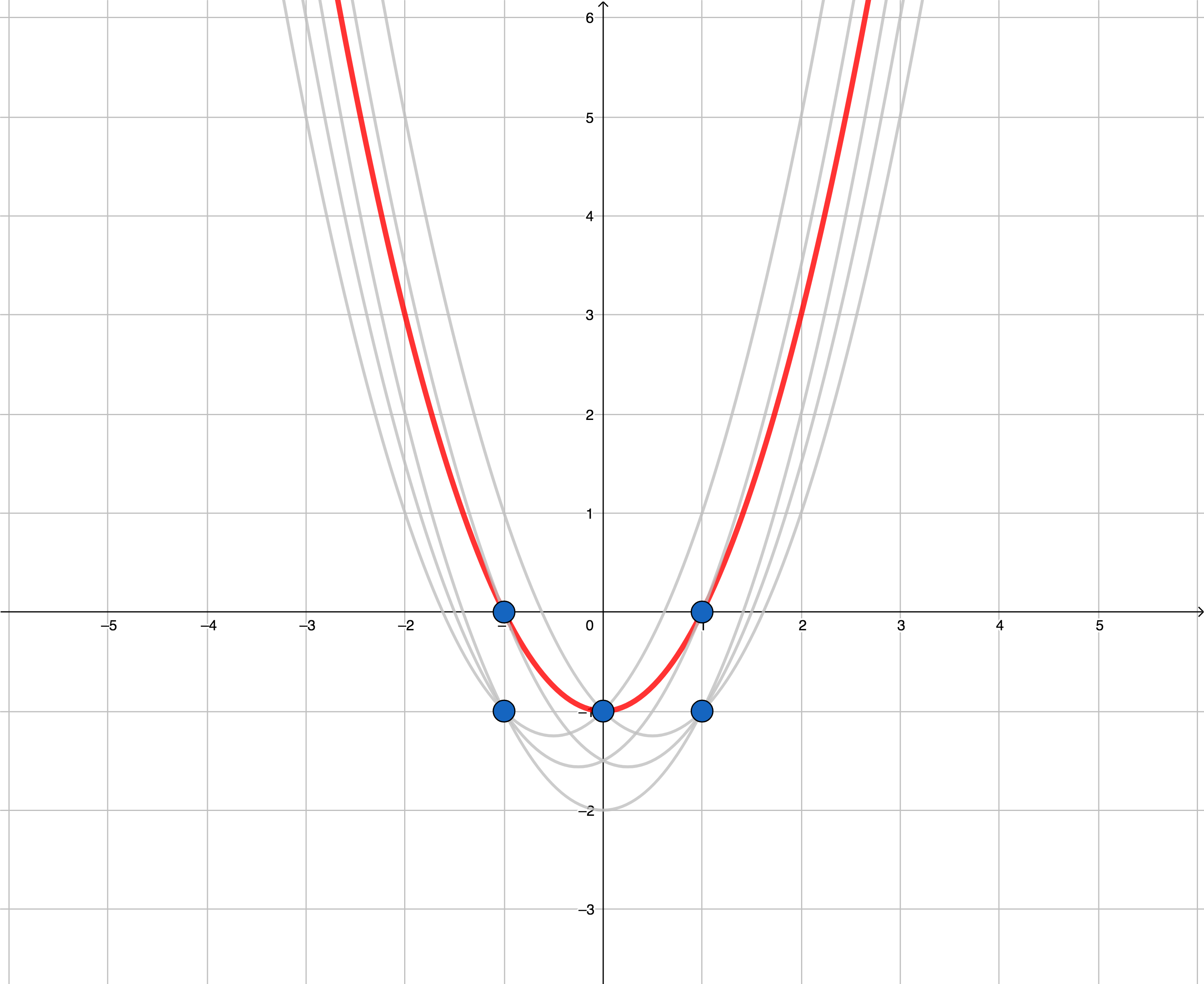Второй пример.
