Есть взвешенное дерево с $$$n$$$ вершинами и $$$n-1$$$ ребрами. Вершины пронумерованные от $$$1$$$ до $$$n$$$. Веса ребер — положительные целые числа не превышающее $$$100$$$. Определим расстояние между двумя вершинами как сумму ребер на уникальном пути между ними. Вы хотели бы найти диаметр дерева. Диаметр — это максимальное расстояние между вершинами.
К сожалению, дерево вам неизвестно, но вы можете задать несколько вопросов. В одном вопросе вы можете указать два непустых непересекающихся набора вершин $$$p$$$ и $$$q$$$, и вам скажут максимальное расстояние между одной вершиной в $$$p$$$ и одной вершиной в $$$q$$$. Другими словами, максимальное расстояние между $$$x$$$ и $$$y$$$, где $$$x \in p$$$ и $$$y \in q$$$. Задав не более $$$9$$$ вопросов, вы должны найти максимальное расстояние между любой парой вершин.
Во входных данных находятся несколько (не меньше одного) тестовых случаев. В первой строке находится одно целое число $$$t$$$ ($$$1 \le t \le 1\,000$$$) — количество тестовых случаев. Далее следуют описания тестовых случаев.
Первая строка описания тестового случая содержит одно целое число $$$n$$$ ($$$2 \leq n \leq 100$$$) — количество вершин в дереве.
Чтобы задать вопрос, выведите «$$$k_1\ k_2\ a_1\ a_2\ \ldots\ a_{k_1}\ b_1\ b_2\ \ldots\ b_{k_2}$$$» $$$(k_1, k_2 \geq 1$$$ и $$$k_1+k_2 \leq n$$$). Эти два множества не должны быть пусты и не должны пересекаться. В ответ считайте одно целое число $$$\max_{p,q} dist(a_p, b_q)$$$. Если вы когда-либо получите $$$-1$$$, немедленно завершите вашу программу, чтобы избежать других вердиктов.
После вывода запроса не забудьте вывести перевод строки и сбросить буфер вывода. В противном случае вы получите вердикт Решение «зависло». Для сброса буфера используйте:
- fflush(stdout) или cout.flush() в C++;
- System.out.flush() в Java;
- flush(output) в Pascal;
- stdout.flush() в Python;
- смотрите документацию для других языков.
Когда вы будете готовы ответить, выведите «$$$-1\ d$$$», где $$$d$$$ — максимальное кратчайшее расстояние по всем парам вершин.
Вы можете задать не более $$$9$$$ вопросов в каждом тесте.
Формат для взломов
Чтобы взломать, используйте следующий формат. Обратите внимание, что вы можете взламывать, используя только один тест.
Первая строка должна содержать одно целое число $$$t$$$ ($$$t=1$$$).
Вторая строка должна содержать одно целое число $$$n$$$ ($$$2 \leq n \leq 100$$$).
Каждая из следующих $$$n-1$$$ строк должна содержать три целых числа $$$a_i, b_i, c_i$$$ ($$$1\leq a_i, b_i\leq n$$$, $$$1 \leq c_i \leq 100$$$). Они описывают неориентированное ребро между вершинами $$$a_i$$$ и $$$b_i$$$ с весом $$$c_i$$$. Эти ребра должны образовывать дерево.
2 5 9 6 10 9 10 2 99
1 4 1 2 3 4 5 1 4 2 3 4 5 1 1 4 3 4 5 1 2 1 4 4 5 1 2 3 1 4 5 1 2 3 4 -1 10 1 1 1 2 -1 99
В первом примере первое дерево выглядит так: 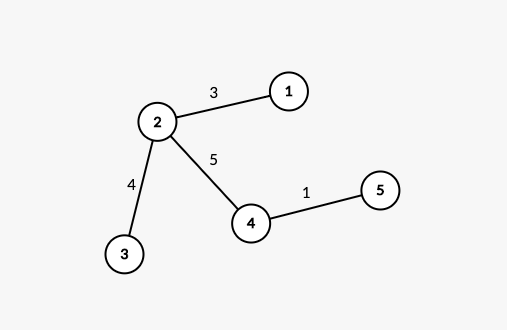
В первом вопросе $$$p = {1}$$$ и $$$q = {2, 3, 4, 5}$$$. Максимальное расстояние между вершинами в $$$p$$$ и вершинами $$$q$$$ равно $$$9$$$ (расстояние между вершинами $$$1$$$ и $$$5$$$).
Второе дерево — это дерево с двумя вершинами и ребром с весом $$$99$$$ между ними.
| Название |
|---|




