Вам дан полный двудольный граф с $$$2n$$$ вершинами, с $$$n$$$ вершинами в каждой доле. Вершины от $$$1$$$ до $$$n$$$ находятся в одной доле, а вершины от $$$n+1$$$ до $$$2n$$$ — в другой. Вам также дается $$$n \times n$$$ матрица $$$a$$$, описывающая веса ребер. $$$a_{ij}$$$ обозначает вес ребра между вершинами $$$i$$$ и $$$j+n$$$. Каждое ребро имеет определенный вес.
Алиса и Боб играют в игру на этом графе. Сначала Алиса выбирает для себя способ игры либо «увеличение», либо «уменьшение», а Боб получает то, что не выбрала Алиса. Затем она помещает фишку в любую вершину графа. После чего Боб перемещает фишку по любому ребру, которое выходит из этой вершины. Теперь они по очереди играют в следующую игру, в которой Алиса ходит первой.
Текущий игрок должен переместить фишку из текущей вершины в некоторую соседнюю не посещенную вершину. Пусть $$$w$$$ будет вес последнего пройденного ребра. Вес следующего ребра должен быть строго больше, чем $$$w$$$, если игрок играет за «увеличение», в противном случае он должен быть строго меньше. Первый игрок, который не может сделать ход, проигрывает.
Вам даны $$$n$$$ и веса ребер графа. Вы можете играть за Алису или Боба, и вы будете играть против тестирующей программы. Вы должны выиграть все игры.
Во входных данных находятся несколько (не меньше одного) тестовых случаев. В первой строке находится одно целое число $$$t$$$ ($$$1 \le t \le 50$$$) — количество тестовых случаев. Далее следуют описания тестовых случаев.
Первая строка описания тестового случая содержит одно целое число $$$n$$$ ($$$1 \leq n \leq 50$$$) — количество вершин в каждой доле.
Каждая из следующих $$$n$$$ строк содержит $$$n$$$ целых чисел $$$a_{ij}$$$ ($$$1 \leq a_{ij} \leq n^2$$$). $$$a_{ij}$$$ обозначает вес ребра между вершиной $$$i$$$ и вершиной $$$j+n$$$. Гарантируется, что все $$$a_{ij}$$$ различны.
Сначала выведите «A» или «B», этот символ обозначает за какого игрока вы хотите играть («A» за Алису и «B» за Боба).
Если вы играете за Алису, выведите либо «I», либо «D» (обозначает способ игры «увеличение» («I») или «уменьшение» («D»). После этого выведите вершину, в которой вы хотите начать игру.
Если вы играете за Боба, считайте символ «I» или «D» (обозначает способ игры, который выбрала тестирующая программа), после этого считайте вершину, которую тестирующая программа выбрала для начала.
Чтобы сделать ход, выведите номер вершины, к которой вы хотите перейти. Чтобы понять, куда переходит ваш противник, считайте одно целое число — номер вершины куда он переходит.
Если вы считали $$$-1$$$, это значит, что у вашего противника нет возможных ходов (или он просто сдался), и что вы выиграли игру. Немедленно прекратите эту игру и начните играть в следующую.
Если вы считали $$$-2$$$, это значит, что у вас неправильный запрос, и вам нужно немедленно прекратить вашу программу, чтобы избежать других вердиктов.
Если вы не можете походить или сдались, выведите $$$-1$$$ и немедленно прекратите вашу программу. В таком случае вы получите вердикт Неправильный ответ.
После вывода запроса не забудьте вывести перевод строки и сбросить буфер вывода. В противном случае вы получите вердикт Решение «зависло». Для сброса буфера используйте:
- fflush(stdout) или cout.flush() в C++;
- System.out.flush() в Java;
- flush(output) в Pascal;
- stdout.flush() в Python;
- смотрите документацию для других языков.
Формат для взломов
Чтобы взламывать, используйте следующий формат. Обратите внимание, что вы можете взламывать только одним тестом.
Первая строка должна содержать одно целое число $$$t$$$ ($$$t=1$$$).
Вторая строка должна содержать одно целое число $$$n$$$ ($$$1 \leq n \leq 50$$$).
Каждая из следующих $$$n$$$ строк должна содержать $$$n$$$ целых чисел $$$a_{ij}$$$ ($$$1 \leq a_{ij} \leq n^2$$$). $$$a_{ij}$$$ обозначает вес ребра между вершиной $$$i$$$ и вершиной $$$j+n$$$. Все $$$a_{ij}$$$ должны быть различны.
В этом случае проверяющая программа будет использовать случайный валидный ход против решения. Если у нее не останется валидных ходов, она объявит игрока победителем.
2 3 3 1 9 2 5 7 6 4 8 6 -1 1 1 I 1 -1
A D 3 2 B 2
Первый пример содержит два случая. В первом случае граф выглядит следующим образом.
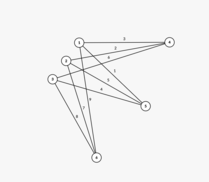
В примере игрок решает играть за Алису и выбирает «уменьшение» и начинает с вершины $$$3$$$. Проверяющая система отвечает, двигаясь к вершине $$$6$$$. После этого игрок перемещается в вершину $$$2$$$. В этот момент у проверяющей программы больше нет ходов (поскольку вес должен «увеличиться»), поэтому она сдается и выводит $$$-1$$$.
В следующем случае у нас есть две вершины, соединенные ребром с весом $$$1$$$. Игрок решает играть за Боба. Независимо от того, что выберет проверяющая система, игрок может переместить фишку в другую вершину, и у проверяющей программы не будет ходов, поэтому она проиграет.
| Название |
|---|




