| Codeforces Beta Round 87 (Div. 1 Only) |
|---|
| Закончено |
Маленький Джон мечтает стать водопроводчиком. Сегодня он нарисовал клетчатое поле размером n × m, состоящее из n строк и m столбцов.
В каждой клетке Джон хочет нарисовать фрагмент трубы. Он умеет рисовать фрагменты четырех типов, которые нумеруются от 1 до 4 как показано на картинке:
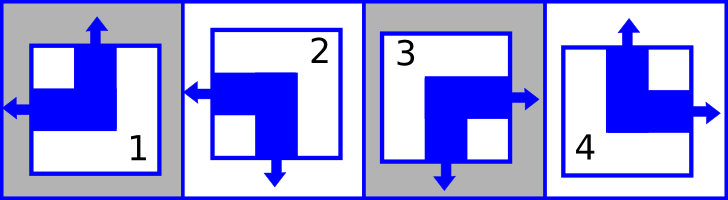
Каждый фрагмент трубы имеет два конца, они обозначены стрелками на картинке. Например, концы фрагмента номер 1 направлены влево и вверх.
Маленький Джон считает, что система труб протекает, если хотя бы один конец одного фрагмента не подсоединен ни к другому концу, ни к краю поля. Ниже приведены примеры двух систем труб размера 1 × 2. Система труб в левом примере протекает, в правом — не протекает.
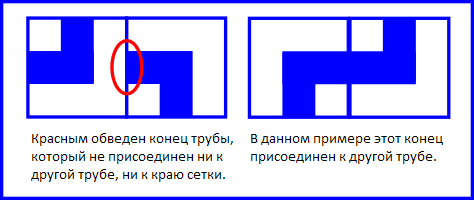
Маленький Джон уже начал рисовать трубы. Вам дано поле, каждая клетка которого либо содержит один из четырех фрагментов трубы, либо пуста. Найдите количество способов нарисовать во всех пустых клетках фрагменты трубы так, чтобы получившаяся система труб не протекала. Выведите это число по модулю 1000003 (106 + 3).
Учтите, что повороты и отражения поля не разрешаются. То есть если два способа равны только после поворота или отражения, то эти способы следует считать различными.
В первой строке через пробел записаны два целых числа n и m (1 ≤ n, m, n·m ≤ 5·105) — количество строк и столбцов соответственно. Далее следует n строк по m символов — описание поля. Один символ описывает одну клетку:
- «1» - «4» — фрагмент трубы одного из четырех типов, описанных выше
- «.» — пустая клетка
Выведите одно число — количество способов завершить рисунок так, чтобы система труб не имела протечек, по модулю 1000003 (106 + 3). Если это сделать невозможно, выведите 0.
2 2
13
..
2
3 1
1
4
.
0
2 2
3.
.1
1
В первом примере начальная конфигурация труб выглядит следующим образом:
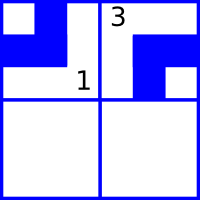
Два способа завершить рисунок:
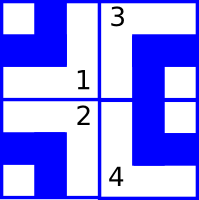

Во втором примере начальная конфигурация сразу протекает, поэтому невозможно завершить рисунок так, чтобы получившаяся система труб не протекала.
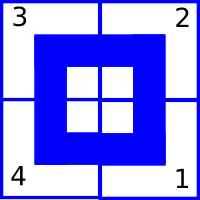
В последнем примере возможна одна система труб без протечек:
| Название |
|---|




