| Codeforces Round 551 (Div. 2) |
|---|
| Закончено |
Теперь Сервал — младший ученик средней школы Джапари, и он все еще в восторге от математики, как и раньше.
Как математически талантливый мальчик, он любит играть с числами. На этот раз он хочет поиграть с числами на подвешенном дереве.
Деревом называется связный граф без циклов. Подвешенное дерево имеет выделенную вершину, называемую корнем. Родителем вершины $$$v$$$ называется последняя отличная от $$$v$$$ вершина на пути от корня к вершине $$$v$$$. Дети вершины $$$v$$$ — все вершины, для которых $$$v$$$ является родителем. Вершина называется листом, если у нее нет детей.
Подвешенное дерево Сервала имеет $$$n$$$ вершин, корень дерева — вершина $$$1$$$. Сервал хочет написать по одному числу в каждую из вершин, но есть некоторые ограничения. В каждой из вершин, кроме листьев, записана операция $$$\max$$$ или $$$\min$$$, указывающая, что число в этой вершине должно быть равно максимуму или минимуму среди всех чисел, написанных в ее детях, соответственно.
Предположим, что в дереве $$$k$$$ листьев. Сервал хочет написать числа $$$1, 2, \ldots, k$$$ в эти $$$k$$$ листьев (каждое число должно использоваться ровно один раз). Он любит большие числа, поэтому он хочет максимизировать число в корне. Как его лучший друг, вы можете помочь ему?
Первая строка содержит целое число $$$n$$$ ($$$2 \leq n \leq 3\cdot 10^5$$$) — количество вершин в дереве.
Вторая строка содержит $$$n$$$ целых чисел, $$$i$$$-е из них описывает операцию на вершине $$$i$$$. $$$0$$$ обозначает $$$\min$$$ и $$$1$$$ обозначает $$$\max$$$. Если вершина является листом, будет записано $$$0$$$ или $$$1$$$, но вы можете игнорировать это число.
Третья строка содержит $$$n-1$$$ целое число $$$f_2, f_3, \ldots, f_n$$$ ($$$1 \leq f_i \leq i-1$$$), где $$$f_i$$$ обозначает родителя вершины $$$i$$$.
Выведите одно целое число — максимальное значение числа в корне, которое Сервал может получить.
6 1 0 1 1 0 1 1 2 2 2 2
1
5 1 0 1 0 1 1 1 1 1
4
8 1 0 0 1 0 1 1 0 1 1 2 2 3 3 3
4
9 1 1 0 0 1 0 1 0 1 1 1 2 2 3 3 4 4
5
Примеры показаны на рисунках ниже. Числа, написанные в середине вершин, являются их номерами, а сверху написаны числа, которые пишет Сервал.
В первом примере, независимо от того, как вы расположите числа, ответ будет $$$1$$$.

Во втором примере, независимо от того, как вы расположите числа, ответ будет $$$4$$$.
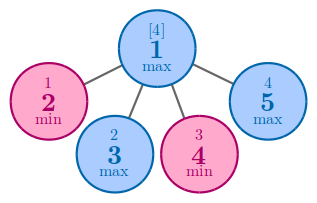
В третьем примере одним из оптимальных решений для достижения $$$4$$$ является расстановка чисел $$$4$$$ и $$$5$$$ на вершины $$$4$$$ и $$$5$$$.
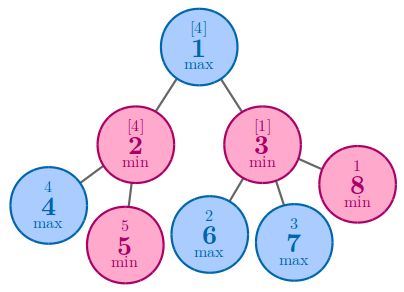
В четвертом примере оптимальным решением является поставить число $$$5$$$ на вершину $$$5$$$.
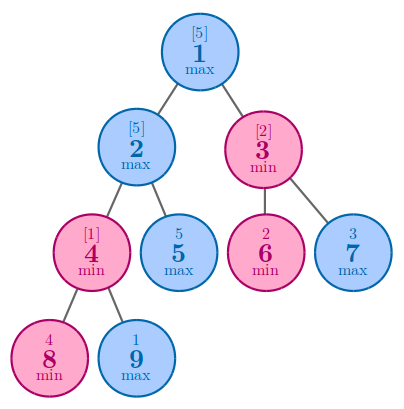
| Название |
|---|




