| Codeforces Round 551 (Div. 2) |
|---|
| Закончено |
Это интерактивная задача.
Сейчас Сервал ученик старшей школы Джапари. На пути в школу он должен пройти через пруд, в котором обитает опасная змея! Пруд можно описать таблицей $$$n \times n$$$. У змеи есть голова и хвост, которые находятся в разных клетках, а ее тело — это последовательность соседних клеток, соединяющих голову и хвост, без самопересечений. Если Сервал зайдет в клетку с головой или в клетку с хвостом, змея укусит его и он умрет.
К счастью, у него есть специальное оборудование, которое может отвечать на следующий вопрос: вы можете выбрать прямоугольник, и оно скажет вам, сколько раз вы пересечете границу прямоугольника, если вы пройдете по змее от ее головы до хвоста. На иллюстрациях ниже изображена возможная змея и возможный запрос к ней, ответ на который равен $$$4$$$.
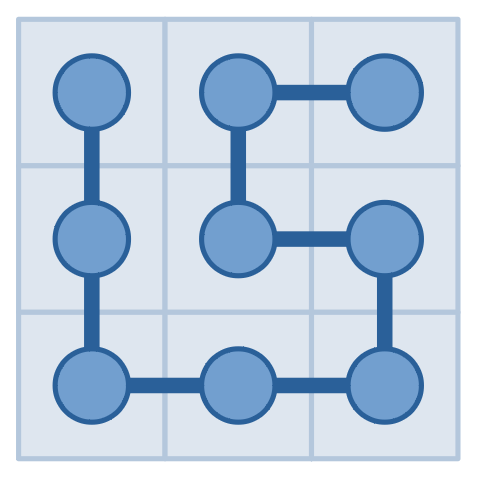
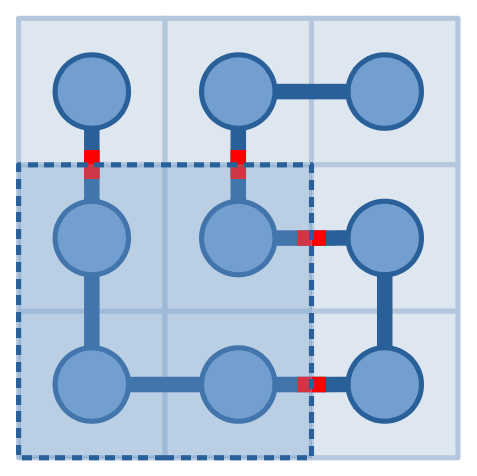
Сегодня Сервал проснулся слишком поздно и у него хватит времени только на то, чтобы задать $$$2019$$$ запросов. Как его лучший друг, может быть, вы ему поможете определить положения головы и хвоста?
Две клетки считаются соседними тогда и только тогда, когда у них есть общее ребро таблицы. Змея может иметь тело длины $$$0$$$, что означает, что у нее есть только соседние голова и тело.
Во время ваших запросов змея спит и не движется. Кроме того, очевидно, что положение змеи не зависит от ваших запросов.
В первой строке входного файла записано одно целое число $$$n$$$ ($$$2\leq n \leq 1000$$$) — размер таблицы.
Когда ваша программа готова вывести ответ, выведите ! x1 y1 x2 y2, где $$$(x_1, y_1)$$$ обозначает позицию головы, а $$$(x_2,y_2)$$$ обозначает позицию хвоста. Вы можете вывести голову и хвост в любом порядке.
Чтобы задать запрос, вы должны вывести ? x1 y1 x2 y2 ($$$1 \leq x_1 \leq x_2 \leq n$$$, $$$1\leq y_1 \leq y_2 \leq n$$$), описывая прямоугольник, содержащий все клетки $$$(x,y)$$$ с $$$x_1 \leq x \leq x_2$$$ и $$$y_1 \leq y \leq y_2$$$.Затем считайте одно число — ответ на запрос.
После вывода запроса не забудьте вывести перевод строки и сбросить буфер вывода. В противном случае вы получите вердикт Решение «зависло». Для сброса буфера используйте:
- fflush(stdout) или cout.flush() в C++;
- System.out.flush() в Java;
- flush(output) в Pascal;
- stdout.flush() в Python;
- смотрите документацию для других языков.
Ответ $$$-1$$$ вместо корректного означает, что ваша программа сделала некорректный запрос или превысила ограничение на число запросов. Ваша программа должна немедленно завершиться после прочтения ответа $$$-1$$$, вы получите вердикт Неправильный ответ. В противном случае вы можете получить любой вердикт, так как программа продолжит чтение из закрытого потока.
Если ваша программа неправильно определит голову или хвост змеи, вы также получите врдикт «Неправильный ответ».
Взломы
Чтобы сделать взлом, выведите одно целое число $$$n$$$ ($$$2 \leq n \leq 1000$$$) на первой строке, описывающее размер таблицы.
Во второй строке выведите целое число $$$k$$$ ($$$2 \leq k \leq n^2$$$), описывающее длину змеи.
Затем в $$$k$$$ строках выведите $$$k$$$ пар целых чисел $$$x_i, y_i$$$ ($$$1 \leq x_i, y_i \leq n$$$), каждую пару следует выводить на новой строке, описывая $$$i$$$-ю клетку змеи. Все соседние пары должны быть соседними в таблице, и все $$$k$$$ клеток должны быть различны.
2 1 0 0
? 1 1 1 1 ? 1 2 1 2 ? 2 2 2 2 ! 1 1 2 1
3 2 0
? 2 2 2 2 ? 2 1 2 3 ! 2 1 2 3
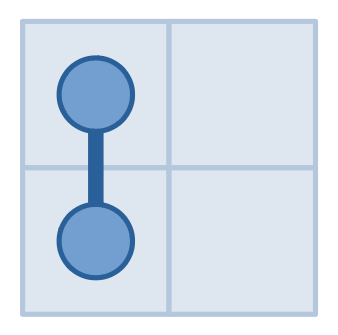
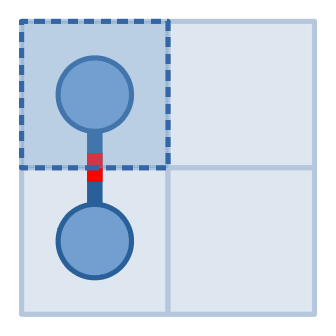
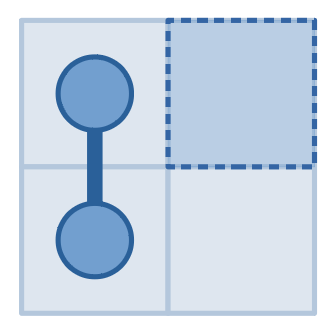
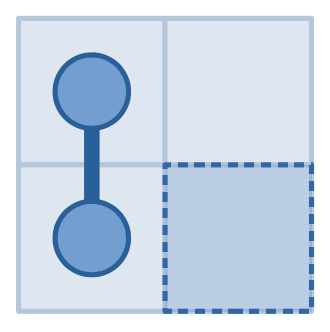
На иллюстрациях выше изображены наши запросы и ответы на них из первого примера. Сначала мы спросили клетку $$$(1,1)$$$ и получили ответ $$$1$$$, затем поняли, что она должна быть соединена ровно с одной другой клеткой. Затем мы спросили $$$(1,2)$$$, и получили ответ $$$0$$$, что значит, что в этой клетке нет змеи совсем. Это значит, что клетка, соседняя с $$$(1,1)$$$, должна быть $$$(2,1)$$$. Затем мы сделали запрос к клетке $$$(2,2)$$$, получили ответ $$$0$$$ и поняли, что змеи также нет в клетке $$$(2,2)$$$. Таким образом змея не выходит из клетки $$$(2,1)$$$, из чего следует, что ответ $$$(1,1)$$$ и $$$(2,1)$$$.
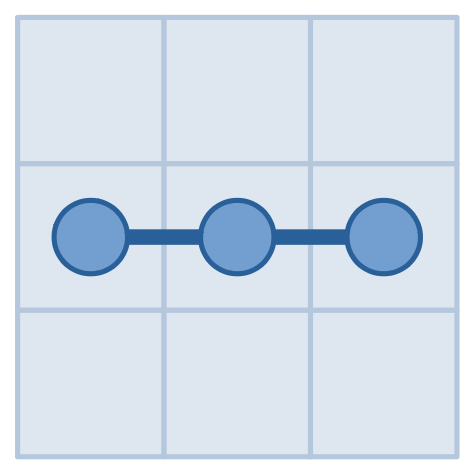
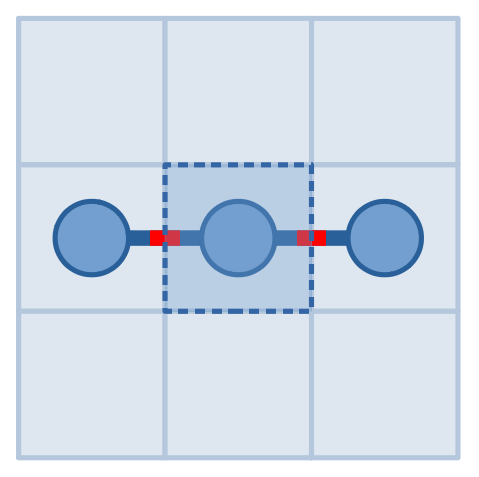
На иллюстрациях выше изображены наши запросы и ответы на них из второго примера. Сделав запрос к клетке $$$(2,2)$$$ и получив $$$2$$$, мы поняли, что змея содержит клетку $$$(2,2)$$$. Затем, спросив прямоугольник от $$$(2,1)$$$ до $$$(2,3)$$$, и получив ответ $$$0$$$, мы поняли, что змея никогда не выходит из прямоугольника от $$$(2,1)$$$ до $$$(2,3)$$$. Так как первый ответ равен $$$2$$$, обе клетки $$$(2,1)$$$ и $$$(2,3)$$$ должны быть внутри змеи, из чего следует, что ответ $$$(2,1)$$$ и $$$(2,3)$$$.
| Название |
|---|




