Нам стало настолько скучно, что мы неожиданно решили обсудить, как бы выглядел фильм «Начало», если бы бюджет на картину был бы невероятно мал.
Первая сцена, которая нам вспомнилась, включала в себя изображение того, как целый город сгибается, и одни здания подминают другие под собой:

Сразу ощущается, что на компьютерную графику для этого уйдет немало денег, не так ли? К счастью, мы придумали аналог этой сцены, который снять гораздо дешевле.
Во-первых, забудьте про 3D, это очень сложно и дорого! Город теперь представляется в виде числовой прямой (бесконечной для простоты, разумеется).
Во-вторых, город совсем не должен выглядеть естественно. На прямой есть $$$n$$$ зданий. Каждое здание — это квадрат $$$1 \times 1$$$. Здания пронумерованы от $$$1$$$ до $$$n$$$ в возрастающем порядке своих позиций. Нижние углы здания $$$i$$$ расположены в точках $$$a_i$$$ и $$$a_i + 1$$$ числовой прямой. Также расстояние между любыми двумя соседними зданиями $$$i$$$ и $$$i + 1$$$ не превышает $$$d$$$ (на самом деле, это условие здесь лишь для того, чтобы город не выглядел сильно разреженным). Расстояние между зданиями $$$i$$$ и $$$i + 1$$$ считается от правого нижнего угла здания $$$i$$$ до левого нижнего угла здания $$$i + 1$$$.
Наконец, изгиб тоже довольно тяжело просимулировать! Будем осуществлять сгиб в некоторой целой координате $$$x$$$ по следующему алгоритму. Возьмем луч из $$$x$$$ в $$$+\infty$$$ и все здания, которые на нем находятся, и начнем поворачивать луч и здания против часовой стрелки относительно точки $$$x$$$. В какой-то момент будет достигнуть угол, на котором некоторое здание коснется либо другого здания, либо части прямой. Необходимо перестать сгибать здесь (реализация разрушения здания уж точно своих денег не стоит).
Назовем угол между двумя лучами в финальном состоянии конечным углом $$$\alpha_x$$$.
Осталось только решить, вокруг какой же целой точки $$$x$$$ лучше всего сгибать. К счастью, мы уже отобрали $$$m$$$ кандидатов для сгиба.
Пожалуйста, помогите нам теперь посчитать конечный угол $$$\alpha_x$$$ для каждого сгиба $$$x$$$ из нашего списка кандидатов.
В первой строке записаны два целых числа $$$n$$$ и $$$d$$$ ($$$1 \le n \le 2 \cdot 10^5$$$, $$$0 \le d \le 7000$$$) — количество зданий и максимальное расстояние между двумя соседними зданиями, соответственно.
Во второй строке записаны $$$n$$$ целых чисел $$$a_1, a_2, \dots, a_n$$$ ($$$a_1 = 0$$$, $$$0 < a_{i + 1} - a_i \le d + 1$$$) — координаты левых углов соответствующих зданий в возрастающем порядке.
В третьей строке записано одно целое число $$$m$$$ ($$$1 \le m \le 2 \cdot 10^5$$$) — количество кандидатов.
В четвертой сроке записаны $$$m$$$ целых чисел $$$x_1, x_2, \dots, x_m$$$ ($$$0 \le x_i \le a_n + 1$$$, $$$x_i < x_{i + 1}$$$) — координаты сгибов, для которых требуется посчитать конечный угол, в возрастающем порядке.
Выведите $$$m$$$ чисел. Для каждого сгиба $$$x_i$$$ выведите конечный угол $$$\alpha_{x_i}$$$ (в радианах).
Ваш ответ будет считаться правильным, если его абсолютная ошибка не превосходит $$$10^{-9}$$$.
Формально, пусть ваш ответ равен $$$a$$$, а ответ жюри равен $$$b$$$. Ваш ответ будет зачтен, если и только если $$$|a - b| \le 10^{-9}$$$.
3 5 0 5 7 9 0 1 2 3 4 5 6 7 8
1.570796326794897 1.570796326794897 0.785398163397448 0.927295218001612 0.785398163397448 1.570796326794897 1.570796326794897 1.570796326794897 1.570796326794897
2 7 0 4 3 1 3 4
1.570796326794897 0.927295218001612 1.570796326794897
5 0 0 1 2 3 4 6 0 1 2 3 4 5
1.570796326794897 3.141592653589793 3.141592653589793 3.141592653589793 3.141592653589793 1.570796326794897
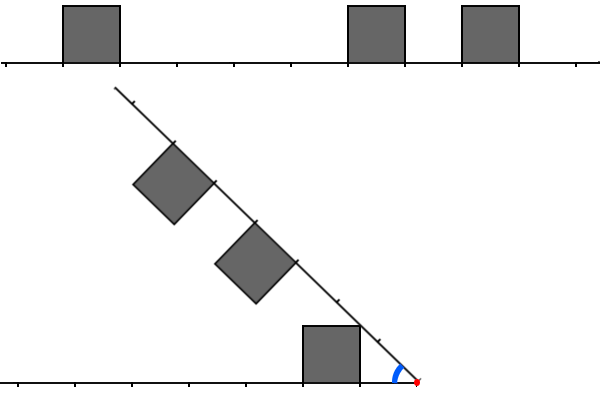
Здесь изображен город из первого примера и сгиб в позиции $$$2$$$ для него. Угол, который необходимо измерить, помечен синим. Можно заметить, что он равен $$$\frac \pi 4$$$.
Также можно заметить, что между любой парой соседних зданий расстояние не превышает $$$4$$$. $$$d = 4$$$ бы тоже подошло в данном тесте.
| Название |
|---|




