| Codeforces Round 564 (Div. 1) |
|---|
| Закончено |
Nauuo — девочка, которая любит играть в игры, связанные с порталами.
Однажды она играла в следующую игру.
В таблице $$$n\times n$$$ строки пронумерованы от $$$1$$$ до $$$n$$$ сверху вниз, столбцы пронумерованы от $$$1$$$ до $$$n$$$ слева направо. Обозначим клетку на пересечении $$$r$$$-й строки и $$$c$$$-го столбца за $$$(r,c)$$$.
Портал — это пара дверей. Из одной из них вы перемещаетесь в другую, не меняя направление вашего движения. Более формально, если вы наступите на клетку с дверью, вас телепортирует на другую клетку того же портала, а затем вы наступите на следующую клетку в исходном направлении. На одной клетке не может быть более одной двери.
«Следующая клетка» — это ближайшая клетка в вашем направлении. Если вы направлены вниз, то следующая клетка для $$$(2,5)$$$ равна $$$(3,5)$$$.
Если вы наступаете на клетку без двери, затем вы обязаны наступить на следующую клетку, не меняя своего направления. Если следующей клетки не существует, вы выйдете из таблицы.
Вы должны расставить несколько (возможно, ноль) порталов в таблице так, что если вы наступите на клетку $$$(i,1)$$$ с направлением вправо, то вы выйдете из таблицы из клетки $$$(r_i,n)$$$, а если вы наступите на клетку $$$(1, i)$$$ с направлением вниз, вы выйдете из таблицы из клетки $$$(n,c_i)$$$.
Гарантируется, что и $$$r_{1..n}$$$, и $$$c_{1..n}$$$ — перестановки из $$$n$$$ элементов. Перестановка из $$$n$$$ элементов это последовательность чисел $$$p_1,p_2,\ldots,p_n$$$ , в которой каждое число от $$$1$$$ до $$$n$$$ встречается ровно один раз.
Nauuo запуталась во время игры, можете ли вы помочь ей с решением?
В первой строке записано одно целое число $$$n$$$ ($$$1\le n\le 1000$$$) — длина стороны таблицы.
Во второй строке записаны $$$n$$$ целых чсиел $$$r_1,r_2,\ldots,r_n$$$ ($$$1\le r_i\le n$$$) — если вы наступите на клетку $$$(i,1)$$$ с направлением вправо, вы должны выйти из клетки $$$(r_i,n)$$$. Гарантируется, что $$$r_{1..n}$$$ — перестановка из $$$n$$$ элементов.
В третьей строке записаны $$$n$$$ целых чисел $$$c_1,c_2,\ldots,c_n$$$ ($$$1\le c_i\le n$$$) — если вы наступите на клетку $$$(1,i)$$$ с направлением вниз, вы должны выйти из клетки $$$(n,c_i)$$$. Гарантируется, что $$$c_{1..n}$$$ — перестановка из $$$n$$$ элементов.
Если невозможно удовлетворить всем условиям, выведите $$$-1$$$.
Иначе в первой строке должно быть записано одно целое число $$$m$$$ ($$$0\le m\le\frac{n^2}2$$$) — количество порталов, которое вы расставили.
В следующих $$$m$$$ строках должны быть записаны по четыре целых числа $$$x_1,y_1,x_2,y_2$$$, обозначающих, что вы поставили портал с дверьми в $$$(x_1,y_1)$$$ и $$$(x_2,y_2)$$$.
Если есть несколько возможных ответов, выведите любой. Вам не обязательно минимизировать $$$m$$$.
3 1 3 2 3 1 2
2 1 1 1 3 2 2 3 1
5 3 1 5 4 2 4 2 1 3 5
3 1 1 3 4 2 2 3 2 2 3 5 1
Пример 1
Портал — это две клетки с одинаковыми буквами. Вы можете расставить порталы следующим образом:
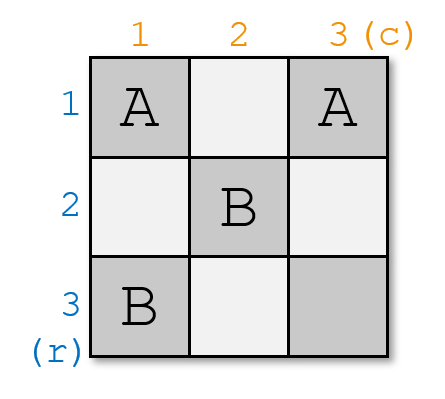
Это удовлетворяет требованиям, потому что:
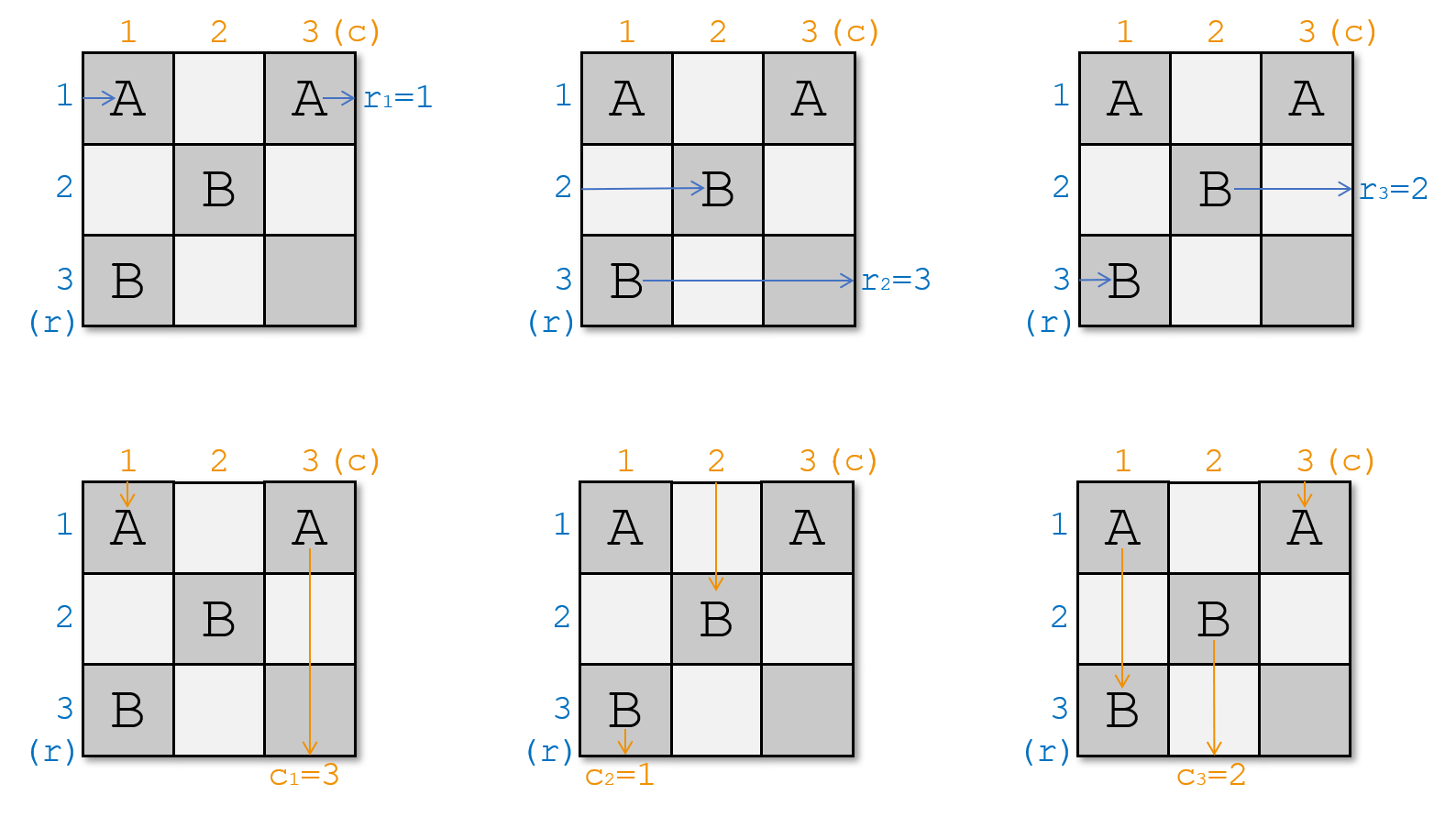
Example 2
Вы можете расставить порталы следующим образом:
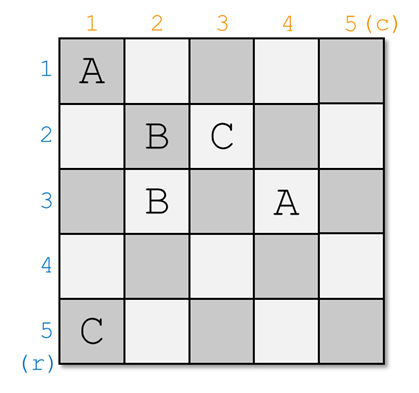
| Название |
|---|




