| Codeforces Round 564 (Div. 1) |
|---|
| Закончено |
Nauuo — девочка, которая любит путешествовать.
Однажды она пришла к дереву, называемому Old Driver Tree, если буквально, то к дереву, на котором был старый водитель.
Дерево — это связный граф с $$$n$$$ вершинами и $$$n-1$$$ ребром. У каждой вершины есть цвет, и Nauuo проедет по простому пути в ODT на машине старого водителя.
Nauuo хочет увидеть много разных цветов на ее пути, но она не знает, по какому простому пути она проедет. Поэтому она просит посчитать вас сумму количества различных цветов по всем различным простым путям. Можете ли вы помочь ей?
Также ODT иногда ремонтируется, поэтому к нему будет произведено $$$m$$$ модификаций, каждая модификация изменяет цвет вершины. Nauuo также хочет узнать ответ после каждой модификации.
Обратите внимания, что в этой задаче мы считаем, что простой путь из $$$u$$$ в $$$v$$$ и простой путь из $$$v$$$ в $$$u$$$ различны тогда и только тогда, когда $$$u\ne v$$$.
В первой строке записаны два целых числа $$$n$$$ и $$$m$$$ ($$$2\le n\le 4\cdot 10^5$$$, $$$1\le m\le 4\cdot 10^5$$$) — количество вершин в дереве и количество модификаций.
Во второй строке записаны $$$n$$$ целых чисел $$$c_1,c_2,\ldots,c_n$$$ ($$$1\le c_i\le n$$$), где $$$c_i$$$ означает исходный цвет вершины $$$i$$$.
В каждой из следующих $$$n-1$$$ строк записаны два целых числа $$$u$$$ и $$$v$$$ ($$$1\le u,v\le n$$$), обозначающие ребро между вершинами $$$u$$$ и $$$v$$$. Гарантируется, что данные ребра образуют дерево.
В каждой из следующих $$$m$$$ строк записаны два целых числа $$$u$$$ и $$$x$$$ ($$$1\le u,x\le n$$$), описывающих модификацию, которая меняет цвет вершины $$$u$$$ на $$$x$$$.
Выведите $$$m+1$$$ целое число — первое из них должно быть равно ответу в начале, остальные должны содержать ответы после модификаций в данном порядке.
5 3 1 2 1 2 3 1 2 1 3 3 4 3 5 3 3 4 1 4 3
47 51 49 45
6 1 1 1 1 1 1 1 1 2 2 3 3 4 4 5 5 6 1 2
36 46
Пример 1
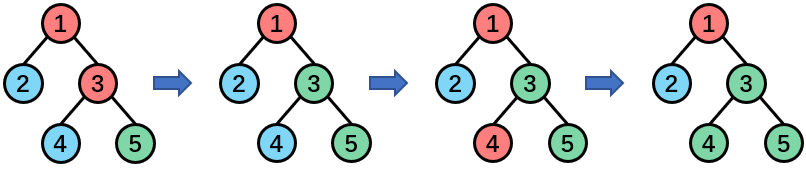
Количество цветов на каждом простом пути в начале:
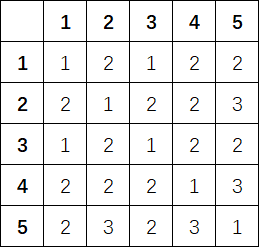
| Название |
|---|




