| Codeforces Round 563 (Div. 2) |
|---|
| Закончено |
Это интерактивная задача.
Вам дано дерево, состоящее из $$$n$$$ вершин, с корнем в вершине $$$1$$$. Дерево — это связный граф без циклов.
Мы выбрали секретную вершину $$$x$$$. Чтобы найти эту вершину, вы можете задавать запросы двух типов:
- d $$$u$$$ ($$$1 \le u \le n$$$). Мы ответим расстоянием между вершинами $$$u$$$ и $$$x$$$. Расстояние между двумя вершинами — это количество ребер в кратчайшем пути между ними.
- s $$$u$$$ ($$$1 \le u \le n$$$). Мы ответим номер второй вершины на пути от $$$u$$$ до $$$x$$$. Тем не менее, есть одна хитрость. Если $$$u$$$ не является предком $$$x$$$, вы получите вердикт «Неправильный ответ»!
Вершина $$$a$$$ называется предком вершины $$$b$$$, если $$$a \ne b$$$ и кратчайший путь от вершины $$$1$$$ к вершине $$$b$$$ проходит через вершину $$$a$$$. Обратите внимание, что в этой задаче вершина не является предком сама себе.
Можете ли вы найти $$$x$$$, сделав не более $$$36$$$ запросов? Скрытая вершина зафиксирована в каждом тесте заранее и не зависит от ваших запросов.
Первая строка содержит одно целое число $$$n$$$ ($$$2 \le n \le 2 \cdot 10^5$$$) — количество вершин в дереве.
Каждая из следующих $$$n-1$$$ строк содержит два целых числа $$$u$$$ и $$$v$$$ ($$$1 \le u,v \le n$$$), которые значат, что между вершинами $$$u$$$ и $$$v$$$ есть ребро. Гарантируется, что граф образует дерево.
Чтобы вывести ответ, выведите «! x» (без кавычек).
Чтобы задать запрос, выведите в одном из двух следующих форматов:
- d $$$u$$$ ($$$1 \le u \le n$$$), или
- s $$$u$$$ ($$$1 \le u \le n$$$).
После каждого вопроса вы должны прочитать ответ: либо расстояние, либо вторую вершину пути, как описано в легенде.
Если мы ответим $$$-1$$$ вместо корректного ответа, это означает, что вы превысили количество запросов, сделали неверный запрос или нарушили условие во втором типе запросов. Завершите вашу программу сразу после получения $$$-1$$$, и вы получите вердикт Wrong answer. В противном случае вы можете получить другой вердикт, потому что ваше решение будет продолжать читать из закрытого потока.
После вывода запроса не забудьте вывести перевод строки и сбросить буфер вывода. В противном случае вы получите вердикт Решение «зависло». Для сброса буфера используйте:
- fflush(stdout) или cout.flush() в C++;
- System.out.flush() в Java;
- flush(output) в Pascal;
- stdout.flush() в Python;
- смотрите документацию для других языков.
Взломы:
Первая строка должна содержать два целых числа $$$n$$$ и $$$x$$$ ($$$2 \le n \le 2 \cdot 10^5$$$, $$$1 \le x \le n$$$).
Каждая из следующих $$$n-1$$$ строк должна содержать два целых числа $$$u$$$ и $$$v$$$ ($$$1 \le u,v \le n$$$), которые значат, что между вершинами $$$u$$$ и $$$v$$$ есть ребро. Граф должен образовать дерево.
5 1 2 1 3 3 4 3 5 3 5
d 2 s 3 ! 5
В первом примере секретной вершиной является вершина $$$5$$$.
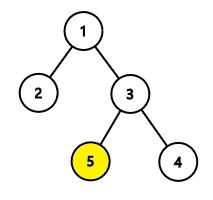
Сначала мы спросим о расстоянии между вершинами $$$x$$$ и $$$2$$$. Ответ $$$3$$$, поэтому вершина $$$x$$$ равна либо $$$4$$$, либо $$$5$$$. Затем мы спрашиваем о второй вершине на пути от вершины $$$3$$$ к вершине $$$x$$$. Обратите внимание, что вершина $$$3$$$ является предком вершины $$$5$$$. Мы получаем вершину $$$5$$$ в качестве ответа. Наконец, мы сообщаем, что секретная вершина — это вершина $$$5$$$.
| Название |
|---|




